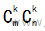克拉克变换(Clarke Transformation)逆变换矩阵的求法

克拉克变换(Clarke Transformation)逆变换矩阵的求法(忽略K选取)

一个平面向量，用a(1,0),b($-\frac{1}{2},\frac{\sqrt{3}}{2}$),c($-\frac{1}{2},-\frac{\sqrt{3}}{2}$)这三个单位向量线性表示，显然有无穷多种解，即某一特解加上N倍的(a+b+c)零向量

根据a,b,c向量的空间对称性可知$a+b+c=0$

$$\begin{gathered} v=k_{a}a+k_{b}b+k_{c}c+N(a+b+c) \\ N\in R \end{gathered}$$
将其用d(1,0),q(0,1)这两个向量表示，显然其表示方法唯一
$$v=k_{d}d+k_{q}q$$

[ k d k q ] = [ 1 − 1 2 − 1 2 0 3 2 − 3 2 ] [ k a k b k c ] \begin{bmatrix} k_d\\ k_q\\ \end{bmatrix}= \begin{bmatrix} 1&-\frac{1}{2}&-\frac{1}{2} \\ 0&\frac{\sqrt{3}}{2}&-\frac{\sqrt{3}}{2}\\ \end{bmatrix} \begin{bmatrix} k_a\\ k_b\\ k_c\\ \end{bmatrix} [kd​kq​​]=[10​−21​23 ​​​−21​−23 ​​​] ​ka​kb​kc​​ ​

变换矩阵不是方阵，不能通过求逆从d和q的系数反过来得到唯一a,b,c的系数

观察变换的过程可以发现，最开始的有效信息只有一个平面向量，在用a，b，c轴表示这个向量时产生了可能的冗余信息，即N倍的零向量

这一部分冗余信息是没有意义的，逆变换的结果只要能得出某一个特解进而反解出这个平面向量即可

逆变换的目的不是为了得到最开始推导出dq系数的a，b，c的系数，而只是为了得到某一个能得到最开始平面向量的a，b，c的系数

第一步，扩充变换矩阵

由于$a+b+c=0$

变换矩阵可扩充为
[ k d k q 0 ] = [ 1 − 1 2 − 1 2 0 3 2 − 3 2 1 1 1 ] [ k a k b k c ] \begin{bmatrix} k_d\\ k_q\\ 0 \end{bmatrix}= \begin{bmatrix} 1&-\frac{1}{2}&-\frac{1}{2} \\ 0&\frac{\sqrt{3}}{2}&-\frac{\sqrt{3}}{2}\\ 1&1&1 \end{bmatrix} \begin{bmatrix} k_a\\ k_b\\ k_c\\ \end{bmatrix} ​kd​kq​0​ ​= ​101​−21​23 ​​1​−21​−23 ​​1​ ​ ​ka​kb​kc​​ ​

第二步，对扩充后的变换矩阵求逆

[ 1 − 1 2 − 1 2 0 3 2 − 3 2 1 1 1 ] − 1 = [ 2 3 0 1 3 − 1 3 3 3 1 3 − 1 3 − 3 3 1 3 ] \begin{bmatrix} 1&-\frac{1}{2}&-\frac{1}{2} \\ 0&\frac{\sqrt{3}}{2}&-\frac{\sqrt{3}}{2}\\ 1&1&1 \end{bmatrix}^{-1} = \begin{bmatrix} \frac{2}{3}&0&\frac{1}{3}\\ -\frac{1}{3}&\frac{\sqrt{3}}{3}&\frac{1}{3}\\ -\frac{1}{3}&-\frac{\sqrt{3}}{3}&\frac{1}{3} \end{bmatrix} ​101​−21​23 ​​1​−21​−23 ​​1​ ​−1= ​32​−31​−31​​033 ​​−33 ​​​31​31​31​​ ​

第三步，对等式两边同时左乘逆阵

[ 2 3 0 1 3 − 1 3 3 3 1 3 − 1 3 − 3 3 1 3 ] [ k d k q 0 ] = [ k a k b k c ] \begin{bmatrix} \frac{2}{3}&0&\frac{1}{3}\\ -\frac{1}{3}&\frac{\sqrt{3}}{3}&\frac{1}{3}\\ -\frac{1}{3}&-\frac{\sqrt{3}}{3}&\frac{1}{3} \end{bmatrix} \begin{bmatrix} k_d\\ k_q\\ 0 \end{bmatrix}= \begin{bmatrix} k_a\\ k_b\\ k_c\\ \end{bmatrix} ​32​−31​−31​​033 ​​−33 ​​​31​31​31​​ ​ ​kd​kq​0​ ​= ​ka​kb​kc​​ ​

第四步，去掉冗余部分

逆阵的第三列与0相乘，对结果无影响，可以把逆阵的第三列和0去掉
[ 2 3 0 − 1 3 3 3 − 1 3 − 3 3 ] [ k d k q ] = [ k a k b k c ] \begin{bmatrix} \frac{2}{3}&0\\ -\frac{1}{3}&\frac{\sqrt{3}}{3}\\ -\frac{1}{3}&-\frac{\sqrt{3}}{3}\\ \end{bmatrix} \begin{bmatrix} k_d\\ k_q\\ \end{bmatrix}= \begin{bmatrix} k_a\\ k_b\\ k_c\\ \end{bmatrix} ​32​−31​−31​​033 ​​−33 ​​​ ​[kd​kq​​]= ​ka​kb​kc​​ ​
左边的2x3矩阵即为逆变换矩阵

当变换矩阵为K倍$\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\end{array}\right]$时，逆变换矩阵为1/K倍 [ 2 3 0 − 1 3 3 3 − 1 3 − 3 3 ] \begin{bmatrix} \frac{2}{3}&0\\ -\frac{1}{3}&\frac{\sqrt{3}}{3}\\ -\frac{1}{3}&-\frac{\sqrt{3}}{3}\\ \end{bmatrix} ​32​−31​−31​​033 ​​−33 ​​​ ​文章来源地址https://www.toymoban.com/news/detail-696716.html

到了这里，关于克拉克变换(Clarke Transformation)逆变换矩阵的求法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！