八大排序算法----堆排序-Toy模板网

这篇具有很好参考价值的文章主要介绍了八大排序算法----堆排序。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

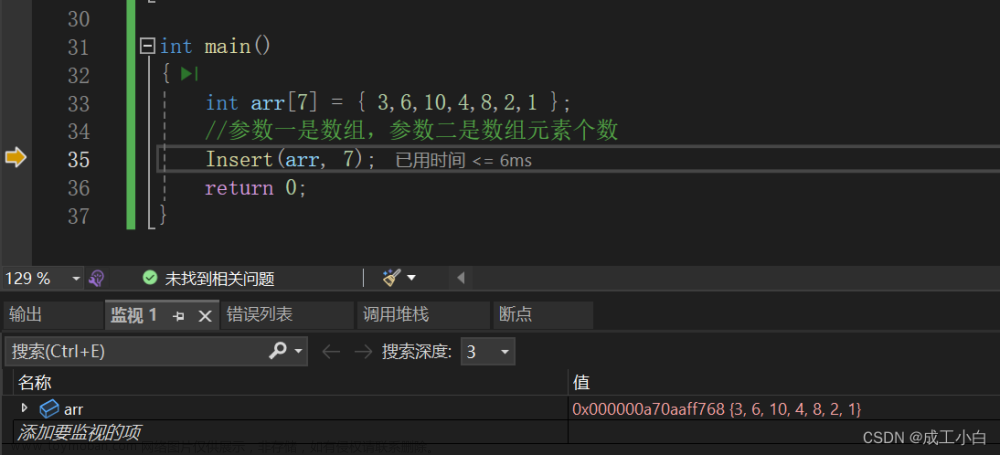
堆排序的基本步骤：（以从大到小的顺序排序为例）

1.构建大顶堆（每个结点的值都大于或等于其左右孩子结点的值）

2.排序：每次堆顶的元素取出来（整个堆中值最大），与最后一个节点做交换，使末尾元素最大

3.交换完之后，需要重新维护堆中剩下的其他节点，保证每次的堆顶都是最大值，重复2，3，直到序列完全有序

Code：

//维护堆的性质
//大顶堆：父节点的左右孩子都比父节点小
//小顶堆：父节点的左右孩子都比父节点大
void heapify(vector<int>& nums, int n, int i)
{
    int large = i;//保存父节点
    int left = 2 * i + 1;//左孩子
    int right = 2 * i + 2;//右孩子
    //判断左孩子是否比父节点大？ 大的话，就更新父节点的下标
    if (left<n && nums[left]>nums[large])
        large = left;
    //判断右孩子是否比父节点大？ 大的话，就更新父节点的下标
    if (right<n && nums[right]>nums[large])
        large = right;
    //到此，已经找到了当前父节点和其左右孩子中最大的节点的下标
    //判断父节点的下标是否发生变化，如果不相等，说明左右孩子中有比父节点大的
    if (large != i)
    {
        //交换节点，维护大顶堆
        swap(nums[large], nums[i]);
        //继续维护剩下的节点
        heapify(nums, n, large);
    }
}
void heapsort(vector<int>& nums, int n)
{
    //建堆：从最后一个有孩子的父节点开始建立
    //这里为什么是i = n / 2 - 1？ 因为左孩子的下标可以表示为2*i+1,此时最后一个孩子的下标为n-1
    //推导过来，找到最后一个有孩子的父节点的下标为n / 2 - 1
    for (int i = n / 2 - 1; i >= 0; i--)
    {
        heapify(nums, n, i);
    }
    //排序：将大顶堆的顶与最后一个叶子节点进行交换，也就是每次找到当前堆中最大的元素，放在数组的最后面
    for (int i = n - 1; i > 0; i--)
    {
        //交换
        swap(nums[i], nums[0]);
        //继续维护大顶堆中剩下节点，要始终保持是大顶堆的顺序
        heapify(nums, i, 0);
    }
}
int main()
{
    int n;
    cin >> n;
    vector<int> nums(n);
    for (int i = 0; i < n; i++)
    {
        cin >> nums[i];
    }
    heapsort(nums, n);
    cout << "按升序顺序排序" << endl;
    for (auto& i : nums)
    {
        cout << i << " ";
    }
    return 0;
}

这里如果要按照从小到大的顺序进行堆排序的话，只需要将维护堆的函数中if判断条件做一点小改动即可。

void heapify(vector<int>& nums, int n, int i)
{
    int small = i;//保存父节点
    int left = 2 * i + 1;//左孩子
    int right = 2 * i + 2;//右孩子
    if (left<n && nums[left]<nums[small])
        small = left;
    if (right<n && nums[right]>nums[small])
        small = right;
    //判断父节点的下标是否发生变化，
    if (small != i)
    {
        //交换节点，维护大顶堆
        swap(nums[small], nums[i]);
        //继续维护剩下的节点
        heapify(nums, n, small);
    }
}

堆排序是不稳定的排序算法。

堆排序的时间复杂度：O（nlogn）文章来源地址https://www.toymoban.com/news/detail-698222.html

到了这里，关于八大排序算法----堆排序的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！