数据结构和算法之二分法查找-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构和算法之二分法查找。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

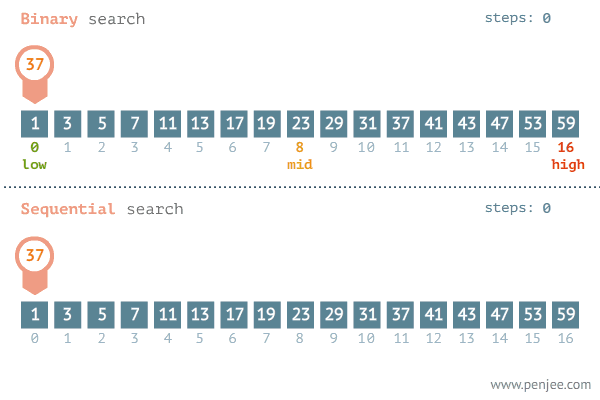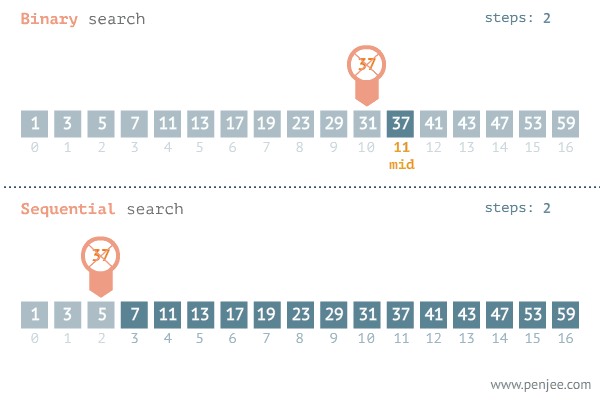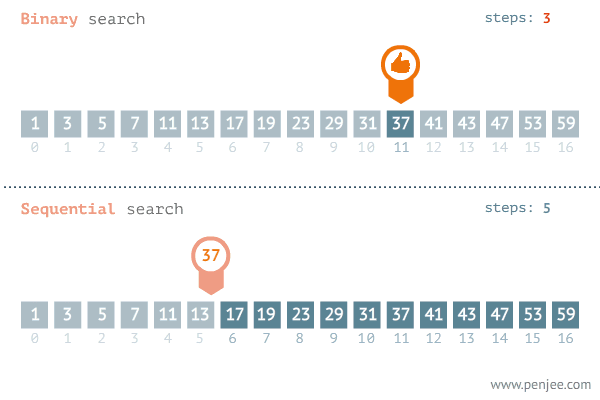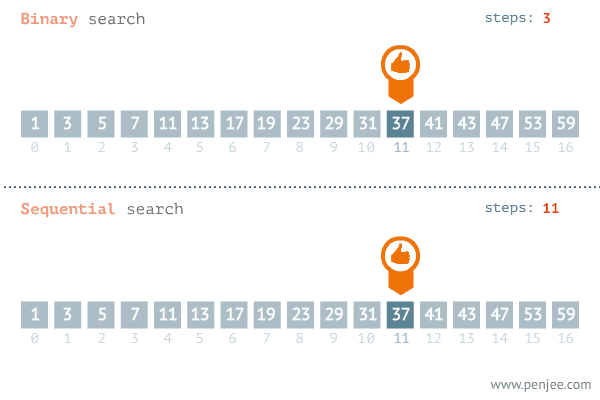
二分法查找，也称作二分查找或折半查找，是一种在有序数组中快速查找特定元素的算法。它采用分治法思想，通过将问题划分为规模更小的子问题，并且通过对子问题的查找来解决原问题。

二分法查找的思路是不断地将数组一分为二，然后判断目标值在哪一部分，进而在该部分继续进行二分查找。具体步骤如下：

首先，设置左边界 left 为0，右边界 right 为数组的长度减1。
然后，计算中间值 mid 为左边界与右边界的平均值，并取整。
接着，比较中间值 arr[mid] 与目标值 target 的大小。如果相等，则返回索引 mid。
如果 arr[mid] 大于 target，说明目标值在左半部分，将右边界 right 更新为 mid-1。
如果 arr[mid] 小于 target，说明目标值在右半部分，将左边界 left 更新为 mid+1。
重复步骤2至5，直到左边界大于右边界，表示数组中无目标值，返回-1。

说明：

开始时，初始化左指针l指向数组的首元素，右指针r指向数组的尾元素。
判断左指针l是否大于右指针r，如果是则表示没有找到目标值，结束查找。
每次都取左指针l和右指针r中间的元素作为中间值。
判断中间值是否等于目标值，如果是则表示找到目标值，结束查找。
如果中间值大于目标值，说明目标值在左半部分，更新右指针r为中间值的前一个位置，继续查找。
如果中间值小于目标值，说明目标值在右半部分，更新左指针l为中间值的后一个位置，继续查找。
继续进行以上步骤，直到找到目标值或者确定没有目标值。

示例代码：

function binarySearch(arr, target) {
   let left = 0; // 定义左边界指针为数组的起始位置
   let right = arr.length - 1; // 定义右边界指针为数组的末尾位置

   while (left <= right) { // 当左边界指针小于等于右边界指针时执行循环
     let mid = Math.floor((left + right) / 2); // 计算中间元素的位置，向下取整

     if (arr[mid] === target) { // 如果中间元素等于目标值
       return mid; // 返回中间元素的位置
     } else if (arr[mid] < target) { // 如果中间元素小于目标值
       left = mid + 1; // 移动左边界指针到中间元素的下一个位置
     } else { // 如果中间元素大于目标值
       right = mid - 1; // 移动右边界指针到中间元素的前一个位置
     }
   }

   return -1; // 如果循环结束仍未找到目标值，则返回-1
}

// 示例使用
let arr = [1, 3, 5, 7, 9];
let target = 5;

let result = binarySearch(arr, target);
console.log(result); // 输出 2

在上面的示例中，提供了一个有序数组 arr 和目标值 target，然后调用 binarySearch 函数进行二分查找。最后输出的结果为目标值在数组中的索引，如果不存在则返回-1。文章来源地址https://www.toymoban.com/news/detail-698258.html