二次型的标准形🎈
- 如果二次型只含有变量的平方项,则称之为二次型的标准形或法式,即 f ( y 1 , ⋯ , y n ) f(y_1,\cdots,y_n) f(y1,⋯,yn)= ∑ i = 1 n k i y i 2 \sum_{i=1}^{n}k_iy_i^2 ∑i=1nkiyi2
标准形的矩阵式
-
f ( y 1 , ⋯ , y n ) = ∑ i n k i y i 2 = ( y 1 , y 2 , ⋯ , y n ) ( k 1 0 ⋯ 0 0 k 2 ⋯ 0 ⋮ ⋮ ⋮ 0 0 ⋯ k n ) ( y 1 y 2 ⋮ y n ) = y T Λ y \begin{aligned} f(y_1,\cdots,y_n) &=\sum_{i}^{n}k_iy_i^2\\ &=(y_1,y_2,\cdots,y_n) \begin{pmatrix} k_{1} &0 &\cdots &0 \\ 0 &k_{2} &\cdots &0 \\ \vdots &\vdots & &\vdots \\ 0 &0 &\cdots &k_{n} \\ \end{pmatrix} \begin{pmatrix} y_{1}\\ y_{2}\\ \vdots \\ y_{n} \\ \end{pmatrix} \\&=\bold{{y}^{T}\Lambda{{y}}} \end{aligned} f(y1,⋯,yn)=i∑nkiyi2=(y1,y2,⋯,yn) k10⋮00k2⋮0⋯⋯⋯00⋮kn y1y2⋮yn =yTΛy
-
可见,标准形的矩阵是对角阵 Λ = diag ( k 1 , ⋯ , k n ) \Lambda=\text{diag}(k_1,\cdots,k_n) Λ=diag(k1,⋯,kn)
-
对角阵的秩 R ( Λ ) R(\bold\Lambda) R(Λ)等于 k 1 , ⋯ , k n k_1,\cdots,k_n k1,⋯,kn中的非零值个数, r ( Λ ) = ∑ k i ≠ 0 1 r(\bold\Lambda)=\sum\limits_{k_i\neq0}1 r(Λ)=ki=0∑1
标准化问题(合同对角化)
- 结合标准形的矩阵式可知,“二次型 f = x T A x f=\bold{x^{T}Ax} f=xTAx经过某个可逆变换 x = C y \bold{x=Cy} x=Cy变成标准形”,就是要使线性变换后的二次型 g = y T D y g=\bold{y^{T}Dy} g=yTDy中的 D = C T A C \bold{D=C^{T}AC} D=CTAC变成一个对角阵 Λ = diag ( k 1 , ⋯ , k n ) \bold{\Lambda}=\text{diag}(k_1,\cdots,k_n) Λ=diag(k1,⋯,kn),也就是将 A \bold{A} A合同对角化
- 更进一步地,将 Λ \bold\Lambda Λ地元素 k i , i = 1 , ⋯ , n k_i,i=1,\cdots,n ki,i=1,⋯,n处理成 − 1 , 0 , 1 -1,0,1 −1,0,1中的元素,称为规范化,详见规范化一文
- Note:合同对角化不是相似对角化
二次型标准化分析🎈
- 如果存在某个可逆阵 P \bold P P使得 P T A P = Λ = diag ( k 1 , ⋯ , k n ) \bold{P^{T}AP={\Lambda}}=\text{diag}(k_1,\cdots,k_n) PTAP=Λ=diag(k1,⋯,kn)即 A \bold{A} A可以合同于某个对角阵 Λ \bold\Lambda Λ,则 f = x T A x f=\bold{x^{T}Ax} f=xTAx可以通过可逆线性变换进行标准化
- 或者说,能够找到可逆矩阵 P \bold{P} P,使得线性变换 x = P y \bold{x=Py} x=Py,能够将二次型 f = x T A x f=\bold{x^{T}Ax} f=xTAx标准化为 g = y T Λ y g=\bold{y^{T}\Lambda{y}} g=yTΛy,其中 Λ \bold\Lambda Λ= P T A P \bold{P^{T}AP} PTAP
二次型可标准化定理
正交相似角度证明
- 由于任意对称阵都合同于某个对角阵,又二次型 f f f的矩阵一定对称阵,所以任何二次型都可以标准化
- 总结为定理:任意二次型
f
=
x
T
A
x
f=\bold{x^{T}A{x}}
f=xTAx总有正交变换
x
=
P
y
\bold{x=Py}
x=Py使得
f
f
f化为标准形
f
=
∑
i
=
1
n
λ
i
y
i
2
f=\sum_{i=1}^{n}\lambda_iy_{i}^{2}
f=∑i=1nλiyi2,且
λ
1
,
⋯
,
λ
n
\lambda_1,\cdots,\lambda_n
λ1,⋯,λn是
A
\bold{A}
A的特征值
- 因为 P \bold{P} P是正交阵 ( P T = P − 1 ) (\bold{P^{T}=P^{-1}}) (PT=P−1),所以相似对角化等价于合同对角化:若 P − 1 A P = Λ \bold{P^{-1}AP=\Lambda} P−1AP=Λ,则 P T A P = Λ \bold{P^{T}AP=\Lambda} PTAP=Λ
- 因此,掌握了对称阵的相似对角化,也就能够通过求解使 A \bold{A} A相似对角化的可逆矩阵 P \bold{P} P来求得使 A \bold{A} A合同对角化的 P \bold{P} P
配方角度证明
-
数域 P P P上任意一个二次型都可以经过非退化(可逆的)线性替换变成平方和形式(标准形)
-
以下证明给出来了一个具体地把二次型化为平方和的方法,和中学里的配方法一样
-
对变量的个数 k k k作数学归纳法
-
对于 k = 1 k=1 k=1,二次型 f = a 11 x 1 2 f=a_{11}x_1^2 f=a11x12,其已经是标准形了
-
现假设 k = n − 1 k=n-1 k=n−1元的二次型定理成立;并设 k = n k=n k=n元的二次型为 f ( x 1 , ⋯ , x n ) f(x_1,\cdots,x_n) f(x1,⋯,xn)= ∑ i = 1 n ∑ j = 1 n a i j x i x j \sum_{i=1}^{n}\sum_{j=1}^{n}a_{ij}x_{i}x_{j} ∑i=1n∑j=1naijxixj, ( a i j = a j i ) (a_{ij}=a_{ji}) (aij=aji)
- f = ( 1 1 ⋯ 1 ) ( a 11 x 1 x 1 a 12 x 1 x 2 ⋯ a 1 n x 1 x n a 21 x 2 x 1 a 22 x 2 x 2 ⋯ a 2 n x 2 x n ⋮ ⋮ ⋮ a n 1 x n x 1 a n 2 x n x 2 ⋯ a n n x n x n ) ( 1 1 ⋮ 1 ) f=\begin{pmatrix} 1&1&\cdots&1 \end{pmatrix} \begin{pmatrix} a_{11}x_1x_1&a_{12}x_1x_2&\cdots&a_{1n}x_1x_n \\ a_{21}x_2x_1&a_{22}x_2x_2&\cdots&a_{2n}x_2x_n \\ \vdots&\vdots&&\vdots\\ a_{n1}x_nx_1&a_{n2}x_nx_2&\cdots&a_{nn}x_nx_n \\ \end{pmatrix} \begin{pmatrix} 1\\1\\\vdots\\1 \end{pmatrix} f=(11⋯1) a11x1x1a21x2x1⋮an1xnx1a12x1x2a22x2x2⋮an2xnx2⋯⋯⋯a1nx1xna2nx2xn⋮annxnxn 11⋮1
-
以下分情况讨论
case1
-
f f f中至少含有一个平方项: ∃ a i i ≠ 0 \exist{\;a_{ii}\neq{0}} ∃aii=0, i ∈ 1 , 2 ⋯ , n i\in{1,2\cdots,n} i∈1,2⋯,n
-
归并所有含有 x i x_i xi的项
-
η i = a i i x i 2 + ∑ j = 1 , j ≠ i n a i j x i x j + ∑ j = 1 , j ≠ i n a j i x j x i = a i i x i 2 + ∑ j = 1 , j ≠ i n 2 a i j x i x j = a i i x i 2 + 2 ( ∑ j = 1 , j ≠ i a i j x j ) x i \eta_i =a_{ii}x_{i}^2+\sum_{j=1,j\neq{i}}^{n}a_{ij}x_ix_j +\sum_{j=1,j\neq{i}}^{n}a_{ji}x_jx_i \\ =a_{ii}x_{i}^2+\sum_{j=1,j\neq{i}}^{n}2a_{ij}x_ix_j \\=a_{ii}x_i^2+2(\sum_{{j=1,j\neq{i}}}a_{ij}x_j)x_i ηi=aiixi2+j=1,j=i∑naijxixj+j=1,j=i∑najixjxi=aiixi2+j=1,j=i∑n2aijxixj=aiixi2+2(j=1,j=i∑aijxj)xi
-
显然 η i \eta_i ηi包含 1 + ( n − 1 ) = n 1+(n-1)=n 1+(n−1)=n个不可合并项
-
f = η i + ∑ r , j ≠ i n a r j x r x j f=\eta_i+\sum_{r,j\neq{i}}^{n}a_{rj}x_rx_j f=ηi+∑r,j=inarjxrxj
-
-
然后进行配方
-
η i = a i i ( x i 2 + 2 1 a i i ( ∑ j = 1 , j ≠ i a i j x j ) x i ) = a i i ( [ x i + 1 a i i ( ∑ j = 1 , j ≠ i a i j x j ) ] 2 − [ 1 a i i ( ∑ j = 1 , j ≠ i a i j x j ) ] 2 ) \begin{aligned} \eta_{i} &=a_{ii}(x_i^2+2\frac{1}{a_{ii}}(\sum_{{j=1,j\neq{i}}}a_{ij}x_j)x_i) \\&=a_{ii} \left( [x_i+\frac{1}{a_{ii}} (\sum\limits_{{j=1,j\neq{i}}}a_{ij}x_j) ]^2 -[\frac{1}{a_{ii}}(\sum\limits_{{j=1,j\neq{i}}}a_{ij}x_j)]^2 \right)\\ \end{aligned} ηi=aii(xi2+2aii1(j=1,j=i∑aijxj)xi)=aii [xi+aii1(j=1,j=i∑aijxj)]2−[aii1(j=1,j=i∑aijxj)]2
-
令 α i = a i i [ x i + 1 a i i ( ∑ j = 1 , j ≠ i a i j x j ) ] 2 \alpha_i=a_{ii}[x_i+\frac{1}{a_{ii}} (\sum\limits_{{j=1,j\neq{i}}}a_{ij}x_j)]^2 αi=aii[xi+aii1(j=1,j=i∑aijxj)]2, β i = a i i [ 1 a i i ( ∑ j = 1 , j ≠ i a i j x j ) ] 2 \beta_i=a_{ii}[\frac{1}{a_{ii}}(\sum\limits_{{j=1,j\neq{i}}}a_{ij}x_j)]^2 βi=aii[aii1(j=1,j=i∑aijxj)]2; γ i = ∑ r , j ≠ i n a r j x r x j \gamma_i=\sum_{r,j\neq{i}}^{n}a_{rj}x_rx_j γi=∑r,j=inarjxrxj
-
则 η i = α i + β i \eta_i=\alpha_i+\beta_i ηi=αi+βi
-
这就将 η i \eta_i ηi改写为仅含平方项的形式,并且 α i , β i \alpha_i,\beta_i αi,βi都是关于 { x 1 , ⋯ , x n } − { x i } \{x_1,\cdots,x_n\}-\{x_i\} {x1,⋯,xn}−{xi}的 n − 1 n-1 n−1元二次型,且 β i \beta_i βi包含了所有 x i 2 x_i^2 xi2之外的所有平方项
- 由归纳假设可知 β i + γ i \beta_i+\gamma_i βi+γi可以被标准化
- f = η i + γ i = α i + β i + γ i f=\eta_i+\gamma_i=\alpha_i+\beta_i+\gamma_i f=ηi+γi=αi+βi+γi也可以被标准化
-
-
为了讨论和书写方便,不妨设 a 11 ≠ 0 a_{11}\neq{0} a11=0,代表这一类情况
- f ( x 1 , ⋯ , x n ) = a 11 x 1 2 + ∑ j = 2 n a i j x 1 x j + ∑ j = 2 n a j i x j x 1 + ∑ i = 2 n ∑ j = 2 n a i j x i x j f(x_1,\cdots,x_n)=a_{11}x_1^{2}+\sum_{j=2}^{n}a_{ij}x_1x_j +\sum_{j=2}^{n}a_{ji}x_jx_1 +\sum_{i=2}^{n}\sum_{j=2}^{n}a_{ij}x_{i}x_{j} f(x1,⋯,xn)=a11x12+j=2∑naijx1xj+j=2∑najixjx1+i=2∑nj=2∑naijxixj
-
配方
-
f = a 11 x 1 2 + 2 ∑ j = 2 n a 1 j x 1 x j + ∑ i = 2 n ∑ j = 2 n a i j x i x j = a 11 ( x 1 2 + 2 a 11 − 1 ∑ j = 2 n a 1 j x 1 x j ) + ∑ i = 2 n ∑ j = 2 n a i j x i x j = a 11 ( x 1 + a 11 − 1 ∑ j = 2 n a 1 j x j ) 2 − a 11 ( a 11 − 1 ∑ j = 2 n a 1 j x j ) 2 + ∑ i = 2 n ∑ j = 2 n a i j x i x j = a 11 ( x 1 + a 11 − 1 ∑ j = 2 n a 1 j x j ) 2 + [ − a 11 − 1 ( ∑ j = 2 n a 1 j x j ) 2 + ∑ i = 2 n ∑ j = 2 n a i j x i x j ] f=a_{11}x_1^2+2\sum_{j=2}^{n}a_{1j}x_1x_j +\sum_{i=2}^{n}\sum_{j=2}^{n}a_{ij}x_{i}x_{j} \\=a_{11}(x_1^2+2a_{11}^{-1}\sum_{j=2}^{n}a_{1j}x_{1}x_{j}) +\sum_{i=2}^{n}\sum_{j=2}^{n}a_{ij}x_{i}x_{j} \\=a_{11}(x_1+a_{11}^{-1}\sum_{j=2}^{n}a_{1j}x_{j})^2- a_{11}(a_{11}^{-1}\sum_{j=2}^{n}a_{1j}x_j)^2 +\sum_{i=2}^{n}\sum_{j=2}^{n}a_{ij}x_{i}x_{j} \\=a_{11}(x_1+a_{11}^{-1}\sum_{j=2}^{n}a_{1j}x_{j})^2 +[-a_{11}^{-1}(\sum_{j=2}^{n}a_{1j}x_j)^2 +\sum_{i=2}^{n}\sum_{j=2}^{n}a_{ij}x_{i}x_{j}] f=a11x12+2j=2∑na1jx1xj+i=2∑nj=2∑naijxixj=a11(x12+2a11−1j=2∑na1jx1xj)+i=2∑nj=2∑naijxixj=a11(x1+a11−1j=2∑na1jxj)2−a11(a11−1j=2∑na1jxj)2+i=2∑nj=2∑naijxixj=a11(x1+a11−1j=2∑na1jxj)2+[−a11−1(j=2∑na1jxj)2+i=2∑nj=2∑naijxixj]
-
令 g ( x 2 , ⋯ , x n ) = − a 11 − 1 ( ∑ j = 2 n a 1 j x j ) 2 + ∑ i = 2 n ∑ j = 2 n a i j x i x j g(x_2,\cdots,x_n)=-a_{11}^{-1}(\sum_{j=2}^{n}a_{1j}x_j)^2 +\sum_{i=2}^{n}\sum_{j=2}^{n}a_{ij}x_{i}x_{j} g(x2,⋯,xn)=−a11−1(∑j=2na1jxj)2+∑i=2n∑j=2naijxixj
- 其中 h 1 ( x 2 , ⋯ , x n ) = − a 11 − 1 ( ∑ j = 2 n a 1 j x j ) 2 h_1(x_2,\cdots,x_n)=-a_{11}^{-1}(\sum_{j=2}^{n}a_{1j}x_j)^2 h1(x2,⋯,xn)=−a11−1(∑j=2na1jxj)2, h 2 ( x 2 , ⋯ , x n ) = ∑ i = 2 n ∑ j = 2 n a i j x i x j h_2(x_2,\cdots,x_n)=\sum_{i=2}^{n}\sum_{j=2}^{n}a_{ij}x_{i}x_{j} h2(x2,⋯,xn)=∑i=2n∑j=2naijxixj是关于 x 2 , ⋯ , x n x_2,\cdots,x_n x2,⋯,xn的 n − 1 n-1 n−1元二次型
- 从而 g ( x 2 , ⋯ , x n ) g(x_2,\cdots,x_n) g(x2,⋯,xn)也是关于 x 2 , ⋯ , x n x_2,\cdots,x_n x2,⋯,xn的 n − 1 n-1 n−1元二次型
-
构造线性变换 y = P x \bold{y=Px} y=Px
-
y 1 = x 1 + ∑ j = 2 n a 11 − 1 a 1 j x j y_1=x_1+\sum_{j=2}^{n}a_{11}^{-1}a_{1j}x_j y1=x1+∑j=2na11−1a1jxj
-
y 2 = x 2 y_2=x_2 y2=x2
-
⋮ \vdots ⋮
-
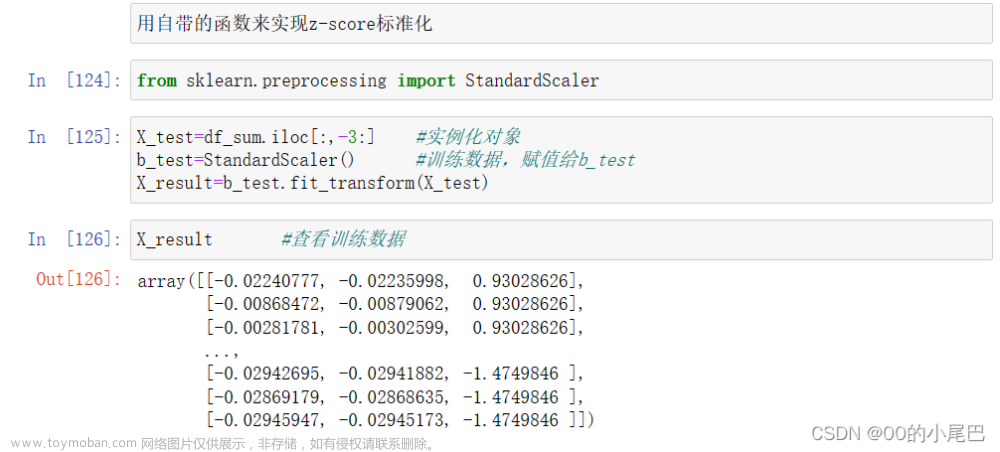
y n = x n y_n=x_n yn=xn
-
变换矩阵:
-
P = ( 1 a 11 − 1 a 11 x 1 ⋯ a 11 − 1 a 1 n x n 0 1 ⋯ 0 0 ⋮ ⋮ 0 0 ⋯ 1 ) \bold P=\begin{pmatrix} 1&a_{11}^{-1}a_{11}x_1&\cdots&a_{11}^{-1}a_{1n}x_n\\ 0&1&\cdots&0\\ 0&\vdots&&\vdots\\ 0&0&\cdots&1 \end{pmatrix} P= 1000a11−1a11x11⋮0⋯⋯⋯a11−1a1nxn0⋮1
-
显然 ∣ P ∣ = 1 ≠ 0 |\bold{P}|=1\neq{0} ∣P∣=1=0,是个可逆变换
-
-
其逆变换 x = P − 1 y \bold{x=P^{-1}y} x=P−1y(将后 n − 1 n-1 n−1个方程回代到第 1 1 1个方程即得)
- x 1 = y 1 − ∑ j = 2 n a 11 − 1 a 1 j x j x_1=y_1-\sum_{j=2}^{n}a_{11}^{-1}a_{1j}x_j x1=y1−∑j=2na11−1a1jxj
- x 2 = y 2 x_2=y_2 x2=y2
- ⋮ \vdots ⋮
- x n = y n x_n=y_n xn=yn
-
则该变换能使 f = a 11 y 1 2 + g ( y 2 , ⋯ , y n ) f=a_{11}y_1^{2}+g({y_2,\cdots,y_n}) f=a11y12+g(y2,⋯,yn)
-
根据归纳假设, g ( y 2 , ⋯ , y n ) g(y_2,\cdots,y_n) g(y2,⋯,yn)可以被标准化,即存在可逆线性变换
(1):-
( y 2 y 3 ⋮ y n ) = ( c 22 c 23 ⋯ c 2 n c 32 c 33 ⋯ c 3 n ⋮ ⋮ ⋱ ⋮ c n 2 c n 3 ⋯ c n n ) ( z 2 z 3 ⋮ z n ) \begin{pmatrix}y_2\\y_3\\\vdots\\y_n\end{pmatrix} =\begin{pmatrix} c_{22}& c_{23}& \cdots & c_{2n} \\ c_{32}& c_{33}& \cdots & c_{3n} \\ \vdots & \vdots & \ddots & \vdots \\ c_{n2}& c_{n3}& \cdots & c_{nn} \end{pmatrix} \begin{pmatrix}z_2\\z_3\\\vdots\\z_n\end{pmatrix} y2y3⋮yn = c22c32⋮cn2c23c33⋮cn3⋯⋯⋱⋯c2nc3n⋮cnn z2z3⋮zn
-
y 2 = c 22 z 2 + ⋯ + c 2 n z n , y 3 = c 32 z 2 + ⋯ + c 3 n z n , ⋮ y n = c n 2 z 2 + ⋯ + c n n z n \begin{aligned} y_{2}&=c_{22} z_{2}+\cdots+c_{2 n} z_{n}, \\ y_{3}&=c_{32} z_{2}+\cdots+c_{3 n} z_{n}, \\ \vdots\\ y_{n}&=c_{n 2} z_{2}+\cdots+c_{n n} z_{n} \end{aligned} y2y3⋮yn=c22z2+⋯+c2nzn,=c32z2+⋯+c3nzn,=cn2z2+⋯+cnnzn
-
此变化能使 g ( y 2 , ⋯ , y n ) g(y_2,\cdots,y_n) g(y2,⋯,yn)= t ( z 2 , ⋯ , z n ) t(z_2,\cdots,z_n) t(z2,⋯,zn)= ∑ j = 2 n d j z j 2 \sum_{j=2}^{n}d_jz_{j}^{2} ∑j=2ndjzj2
-
此时 f = a 11 y 1 2 + ∑ j = 2 n d j z j 2 f=a_{11}y_1^2+\sum_{j=2}^{n}d_jz_{j}^{2} f=a11y12+∑j=2ndjzj2
-
-
基于
(1)追加一条变换: y 1 = z 1 y_1=z_1 y1=z1,得到 n n n元变换(2):-
y 1 = z 1 y 2 = c 22 z 2 + ⋯ + c 2 n z n , y 3 = c 32 z 2 + ⋯ + c 3 n z n , ⋮ y n = c n 2 z 2 + ⋯ + c n n z n \begin{aligned} y_{1}&=z_1\\ y_{2}&=c_{22} z_{2}+\cdots+c_{2 n} z_{n}, \\ y_{3}&=c_{32} z_{2}+\cdots+c_{3 n} z_{n}, \\ \vdots\\ y_{n}&=c_{n 2} z_{2}+\cdots+c_{n n} z_{n} \end{aligned} y1y2y3⋮yn=z1=c22z2+⋯+c2nzn,=c32z2+⋯+c3nzn,=cn2z2+⋯+cnnzn
-
( y 1 y 2 ⋮ y n ) = ( 1 0 ⋯ 0 0 c 22 ⋯ c 2 n 0 c 32 ⋯ c 3 n ⋮ ⋮ ⋱ ⋮ 0 c n 2 ⋯ c n n ) ( z 1 z 2 ⋮ z n ) \begin{pmatrix}y_1\\y_2\\\vdots\\y_n\end{pmatrix} =\begin{pmatrix} 1&0&\cdots&0\\ 0& c_{22}& \cdots & c_{2n} \\ 0& c_{32}& \cdots & c_{3n} \\ \vdots & \vdots & \ddots & \vdots \\ 0& c_{n2}& \cdots & c_{nn} \end{pmatrix} \begin{pmatrix}z_1\\z_2\\\vdots\\z_n\end{pmatrix} y1y2⋮yn = 100⋮00c22c32⋮cn2⋯⋯⋯⋱⋯0c2nc3n⋮cnn z1z2⋮zn
-
-
线性变换
(2)能将 f f f化为标准形 f = ∑ j = 1 n d j z j 2 f=\sum_{j=1}^{n}d_jz_{j}^{2} f=∑j=1ndjzj2 -
由归纳法原理,定理在case1成立
-
-
方法1:
case2
-
若 f f f中不含平方项( x i 2 x_i^2 xi2的系数 a i i = 0 a_{ii}=0 aii=0, i = 1 , ⋯ , n i=1,\cdots,n i=1,⋯,n),但至少存在一个 a i j ≠ 0 a_{ij}\neq{0} aij=0, i ≠ j i\neq{j} i=j
-
则构造关于 y 1 , ⋯ , y n y_1,\cdots,y_n y1,⋯,yn的线性变换 x 1 = y i + y j x_1=y_i+y_j x1=yi+yj, x 2 = y i − y j x_2=y_i-y_j x2=yi−yj, x r = y r , r ≠ i , j x_r=y_r,r\neq{i,j} xr=yr,r=i,j
- 易知该变换矩阵是一个上三角形,其对角线元素之积为1,从而可逆
- 变换{T}能使:
x
i
x
j
=
(
y
i
−
y
j
)
(
y
i
+
y
j
)
=
y
i
2
−
y
j
2
x_ix_j=(y_i-y_j)(y_i+y_j)=y_i^2-y_j^2
xixj=(yi−yj)(yi+yj)=yi2−yj2,即非平方二次项化为平方项组合
- 从而
x
i
x
j
=
(
z
i
+
z
j
)
(
z
i
−
z
j
)
x_ix_j=(z_i+z_j)(z_i-z_j)
xixj=(zi+zj)(zi−zj)=
z
i
2
−
z
j
2
z_i^2-z_j^2
zi2−zj2
- a i j x i x j a_{ij}x_{i}x_j aijxixj= a i j ( z i 2 − z j 2 ) a_{ij}(z_i^2-z_j^2) aij(zi2−zj2)= a i j z i 2 − a i j z j 2 a_{ij}z_i^2-a_{ij}z_j^2 aijzi2−aijzj2
- 所以: f ( x i , ⋯ , x n ) f(x_i,\cdots,x_n) f(xi,⋯,xn)= 2 a i j x i x j + ⋯ 2a_{ij}x_{i}x_j+\cdots 2aijxixj+⋯= 2 a i j z i 2 − 2 a i j z j 2 + ⋯ 2a_{ij}z_i^2-2a_{ij}z_j^2+\cdots 2aijzi2−2aijzj2+⋯
- 从而
x
i
x
j
=
(
z
i
+
z
j
)
(
z
i
−
z
j
)
x_ix_j=(z_i+z_j)(z_i-z_j)
xixj=(zi+zj)(zi−zj)=
z
i
2
−
z
j
2
z_i^2-z_j^2
zi2−zj2
-
这种变换的意义在于将无平方项二次型转换为有平方项二次型,从而将问题转换为第一类情况(case1),即这类二次型仍然可以标准化,即定理在case2也成立
方法2
case2
-
为了方便讨论,不妨再细分为两种子情况,cases2研究第一种,第2种放到caes3中讨论
-
若 a 1 j ≠ 0 , ( j > 1 ) a_{1j}\neq{0},(j>1) a1j=0,(j>1),更进一步地,可以设 a 12 ≠ 0 a_{12}\neq{0} a12=0,这种假设仍然不失一般性
-
执行可逆变换{T}:
-
T : { x 1 = y 1 − y 2 x 2 = y 1 + y 2 x 3 = y 3 ⋮ x n = y n T:\begin{cases} x_1=y_1-y_2\\ x_2=y_1+y_2\\ x_3=y_3\\ \vdots\\ x_n=y_n \end{cases} T:⎩ ⎨ ⎧x1=y1−y2x2=y1+y2x3=y3⋮xn=yn
-
易知该变换矩阵是一个上三角形,其对角线元素之积为1,从而可逆
- 变换{T}能使:
x
i
x
j
=
(
y
i
−
y
j
)
(
y
i
+
y
j
)
=
y
i
2
−
y
j
2
x_ix_j=(y_i-y_j)(y_i+y_j)=y_i^2-y_j^2
xixj=(yi−yj)(yi+yj)=yi2−yj2,即非平方二次项化为平方项组合
- 从而
x
1
x
2
=
(
z
1
+
z
2
)
(
z
1
−
z
2
)
x_1x_2=(z_1+z_2)(z_1-z_2)
x1x2=(z1+z2)(z1−z2)=
z
1
2
−
z
2
2
z_1^2-z_2^2
z12−z22
- a 12 x 1 x 2 a_{12}x_{1}x_2 a12x1x2= a 12 ( z 1 2 − z 2 2 ) a_{12}(z_1^2-z_2^2) a12(z12−z22)= a 12 z 1 2 − a 12 z 2 2 a_{12}z_1^2-a_{12}z_2^2 a12z12−a12z22
- 所以: f ( x 1 , ⋯ , x n ) f(x_1,\cdots,x_n) f(x1,⋯,xn)= 2 a 12 x 1 x 2 + ⋯ 2a_{12}x_{1}x_2+\cdots 2a12x1x2+⋯= 2 a 12 z 1 2 − 2 a 12 z 2 2 + ⋯ 2a_{12}z_1^2-2a_{12}z_2^2+\cdots 2a12z12−2a12z22+⋯
- 从而
x
1
x
2
=
(
z
1
+
z
2
)
(
z
1
−
z
2
)
x_1x_2=(z_1+z_2)(z_1-z_2)
x1x2=(z1+z2)(z1−z2)=
z
1
2
−
z
2
2
z_1^2-z_2^2
z12−z22
- 变换{T}能使:
x
i
x
j
=
(
y
i
−
y
j
)
(
y
i
+
y
j
)
=
y
i
2
−
y
j
2
x_ix_j=(y_i-y_j)(y_i+y_j)=y_i^2-y_j^2
xixj=(yi−yj)(yi+yj)=yi2−yj2,即非平方二次项化为平方项组合
-
-
case3
-
延续cases2中假设 a 1 j ≠ 0 a_{1j}\neq{0} a1j=0,cases3研究其互斥的情况:
-
若 a 1 j = 0 a_{1j}=0 a1j=0, j = 1 , ⋯ , n j=1,\cdots,n j=1,⋯,n
-
根据二次型矩阵的对称性, a j 1 = 0 a_{j1}=0 aj1=0, j = 1 , ⋯ , n j=1,\cdots,n j=1,⋯,n文章来源:https://www.toymoban.com/news/detail-698345.html
-
从而 f ( x 1 , ⋯ , x n ) f(x_1,\cdots,x_n) f(x1,⋯,xn)= ∑ i = 2 n ∑ j = 2 n a i j x i x j \sum_{i=2}^{n}\sum_{j=2}^{n}a_{ij}x_ix_j ∑i=2n∑j=2naijxixj,这是一个 n − 1 n-1 n−1元的二次型,根据归纳假设,它能够标准化文章来源地址https://www.toymoban.com/news/detail-698345.html
到了这里,关于LA@二次型标准形@标准化问题介绍和合同对角化@二次型可标准化定理的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!