斜率优化DP 学习笔记-Toy模板网

这篇具有很好参考价值的文章主要介绍了斜率优化DP 学习笔记。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

动态规划——斜率优化DP

适用情况

适用于求解最优解（最大、最小）问题。

可以将转移方程可以化为 \(\left[\begin{array}{rl} 仅与 \space i \space 有关 & 是我们想要最大/最小化的 \\ 仅与 \space j \space 有关 & 是已知的 \\ 与 \space i \space 和 \space j \space 都有关 & 是两项相乘 \end{array}\right]\) 三部分的，
都可以考虑用斜率优化。

形式化的：原式可化为 \(dp_i = \min\limits_{j \in [l,r]}\{ \mathrm y_j - k_ix_j \} - a_i\)，
其中 \(y\)、\(k\)、\(x\) 均为人为规定与 \(dp\) 和常数有关的式子。

应用

前置知识：初中几何

斜率
已知两个点 \(\text{A}(x_1, y_1)\)，\(\text{B}(x_2, y_2)\)，则直线 \(\text{AB}\) 斜率为 \(\dfrac{y_1 - y_2}{x_1 - x_2}\)。
纵截距
直线 \(y = kx + b\) 的纵截距为 \(b\)；即与 \(y\) 轴交点的纵坐标。
凸壳

求解步骤


设 \(A_i\)、\(B_i\)，使状态转移方程转化为	\(f_i = \min(f_j + (A_i - B_j) ^ 2)\)
当 \(i\) 从 \(j\) 转移来时，丢掉 \(\min\)	\(f_i = f_j + {A_i} ^ 2 + {B_j} ^ 2 - 2 \times A_i \times B_j\)
将仅和 \(j\) 有关的放在左边，其他的放在右边	\(f_j + {B_j} ^ 2 = 2 \times A_i \times B_j + f_i - {A_i} ^ 2\)
设 \(\left\{\begin{array}{ll} y_j &= f_j + {B_j} ^ 2 \\ k_i &= 2 \times A_i \\ x_j &= B_j \\ b_i &= f_i - {A_i} ^ 2 \\ \end{array}\right.\)，原式转换为	\(y_j=k_ix_j+b_i\)
转移方程就写作	\(b_i = \min\{ y_j-k_ix_j \}\)

我们把 \((x_j,y_j)\) 看作二维平面上的点，则 \(k_i\) 表示直线斜率，\(b_i\) 表示一条过 \((x_j,y_j)\) 的斜率为 \(k_i\) 的直线的截距；问题转化为，选择合适的 \(j \in [1, i)\)，最小化直线的截距。

如图，考虑最 native 的算法：我们将这个斜率为 \(k_i\) 的直线从下往上平移，直到有一个点 \((x_p,y_p)\) 在这条直线上，则有 \(b_i=y_p-k_ix_p\)，这时 \(b_i\) 取到最小值。算完 \(f_i\)，我们就把 \((x_i,y_i)\) 这个点加入点集中，以做为新的 DP 决策。那么，我们该如何维护点集？

容易发现，此时，\(b_i\) 所能取到最小值的点一定在下凸壳上。因此在寻找 \(p\) 的时候我们不需要枚举所有 \(i-1\) 个点，只需要考虑凸包上的点。

具体的，设 \(K(a,b)\) 表示过 \((x_a,y_a)\) 和 \((x_b,y_b)\) 的直线的斜率。考虑队列 \(q_l,q_{l+1},\ldots,q_r\)，维护的是下凸壳上的点。

也就是说，对于 \(l<i<r\)，始终有 \(K(q_{i-1},q_i) < K(q_i,q_{i+1})\) 成立；而我们需要找到一个 \(K(q_{e-1},q_e)\le k_i< K(q_e,q_{e+1})\) 的 \(e\)（特别的，当 \(e=l\) 或者 \(e=r\) 时要特别判断）。

一、若 \(k_i\) 关于 \(i\) 单调：

可以单调队列维护凸包。

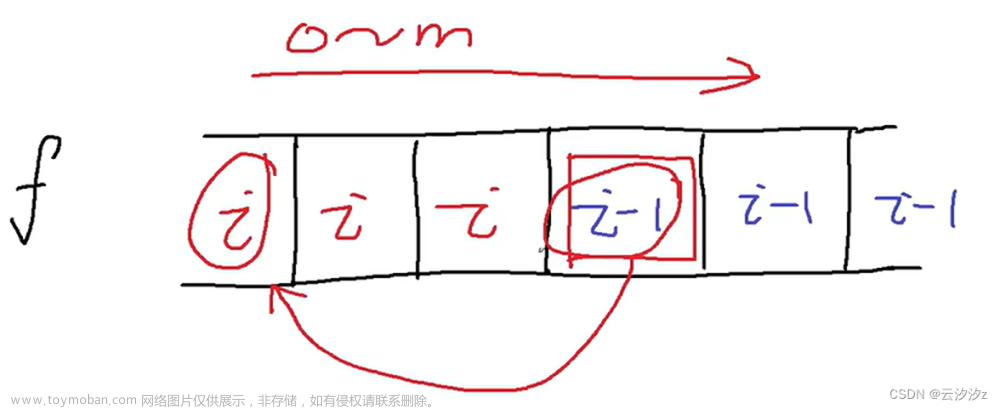
具体的，我们维护一个指针 \(e\) 来计算 \(b_i\) 最小值，即 \(q_e\) 是 \(i\) 的最优决策点，由于 \(k_i\) 是单调的，则 \(e\) 也一定单调，因此 \(e\) 的移动次数是均摊 \(O(1)\) 的。

在插入一个点 \((x_i,y_i)\) 时，我们要判断是否 \(K(q_{r-1},q_r)<K(q_r,i)\)，如果不成立（不形成下凸壳）就将 \(q_r\) 弹出，直到等式满足。然后将 \(i\) 插入到 \(q\) 队尾。

这样我们就将 DP 的复杂度优化到了 \(O(n)\)；最后概括一下上述斜率优化模板题的算法：

将初始状态入队。
每次使用一条和 \(i\) 相关的直线 \(f(i)\) 去切维护的凸包，找到最优决策，更新 \(dp_i\)。
加入状态 \(dp_i\)。如果一个状态（即凸包上的一个点）在 \(dp_i\) 加入后不再是凸包上的点，需要在 \(dp_i\) 加入前将其剔除。

二、若 \(k_i\) 无单调性：

可以在凸壳上二分斜率。

直线的斜率没有单调性，则无法确定 \(q_l\) 是否可以弹出队列。

但是不影响原结构（凸壳）的单调性，因此我们在寻找最优决策点，也就是用直线切凸壳的时候，我们将单调队列找队首改为：凸壳上二分。我们二分查找满足 \(K(q_{e-1},q_e)\le k_i< K(q_e,q_{e+1})\) 那条凸壳边，就可以找到最优决策。

三、若 \(x_i\) 无单调性：

见：CDQ/平衡树优化DP（未整理）。

示例代码

例题：P3195 玩具装箱。

const int N = 5e4 + 10;

int n, l;
int s[N];
int q[N], dp[N];

int Gx(int k1, int k2) { return (2 * s[k1]) - (2 * s[k2]); }
int Gy(int k1, int k2) { return (dp[k1] + s[k1] * s[k1] + 2 * l * s[k1]) - (dp[k2] + s[k2] * s[k2] + 2 * l * s[k2]); }
int Gv(int i, int j) { return dp[j] + (s[i] - s[j] - l) * (s[i] - s[j] - l); }

signed main() {
    scanf("%lld %lld", &n, &l); ++l;
    for (int i = 1; i <= n; ++i) { scanf("%lld", s + i); s[i] += s[i - 1] + 1; }
    int st = 0, ed = 1;
    for (int i = 1; i <= n; ++i) {
        while (st + 1 < ed && Gy(q[st + 1], q[st]) <= s[i] * Gx(q[st + 1], q[st])) ++st;
        dp[i] = Gv(i, q[st]);
        while (st + 1 < ed && Gx(q[ed - 1], q[ed - 2]) * Gy(i, q[ed - 1]) <= Gx(i, q[ed - 1]) * Gy(q[ed - 1], q[ed - 2])) --ed;
        q[ed++] = i;
    } printf("%lld\n", dp[n]);
    return 0;
}