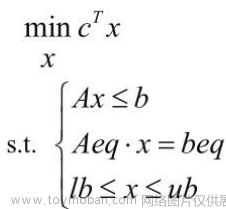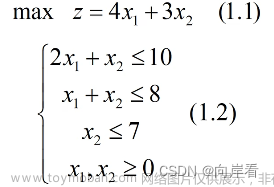数学建模--线性规划方法的Python实现-Toy模板网

这篇具有很好参考价值的文章主要介绍了数学建模--线性规划方法的Python实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1.算法求解问题

2.算法求解思路

3.算法求解代码

4.算法求解结果

1.算法求解问题

求min z=2x1+3x2+x3
s.t:
   x1+4x2+2x3>=8
   3x1+2x2>=6
   x1,x2,x3>=0

2.算法求解思路

关键函数解释如下:
#利用linprogl函数来解决
'''
def linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None,
            bounds=None, method='interior-point', callback=None,
            options=None, x0=None)
求解方式有如下:
LINPROG_METHODS = ['simplex', 'revised simplex', 'interior-point', 'highs', 'highs-ds', 'highs-ipm']
'''

具体解决步骤如下:
#1.分别表示出C,A,B矩阵和bounds即可
#2.A是s.t条件的系数矩阵,而且需要改写成小于等于的形式
#3.B是s.t条件的数值矩阵,而且需要改写成小于等于的形式
#4.bounds表示的是x1,x3,x2的取值范围
#5.调用linprog函数计算结果即可

3.算法求解代码

#Linear Programming Problem 1:
#利用linprogl函数来解决
'''
def linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None,
            bounds=None, method='interior-point', callback=None,
            options=None, x0=None)
求解方式有如下:
LINPROG_METHODS = ['simplex', 'revised simplex', 'interior-point', 'highs', 'highs-ds', 'highs-ipm']
'''

"""
求min z=2x1+3x2+x3
s.t:
   x1+4x2+2x3>=8
   3x1+2x2>=6
   x1,x2,x3>=0
"""
#导入函数和库
import numpy as np
from scipy.optimize import linprog

#分别表示出C,A,B矩阵和bounds即可
C=np.array([2,3,1])#C是2x1+3x2+x3的系数矩阵
#A是s.t条件的系数矩阵,而且需要改写成小于等于的形式
#B是s.t条件的数值矩阵,而且需要改写成小于等于的形式
A=np.array([[-1,-4,-2],[-3,-2,0]])
B=np.array([-8,-6])
#bounds表示的是x1,x3,x2的取值范围
#调用函数计算结果即可
ans=linprog(C,A_ub=A,b_ub=B,method='highs',bounds=((0,None),(0,None),(0,None)))
print(ans)

4.算法求解结果

  算法的求解结果如下所示:
        message: Optimization terminated successfully. (HiGHS Status 7: Optimal)
        success: True（求解结果）
         status: 0
            fun: 7.0(最优值）
              x: [ 8.000e-01  1.800e+00  0.000e+00]（对应的值向量）
            nit: 3（迭代次数）
          lower:  residual: [ 8.000e-01  1.800e+00  0.000e+00]
                 marginals: [ 0.000e+00  0.000e+00  0.000e+00]
          upper:  residual: [       inf        inf        inf]
                 marginals: [ 0.000e+00  0.000e+00  0.000e+00]
          eqlin:  residual: []
                 marginals: []
        ineqlin:  residual: [ 0.000e+00  0.000e+00]
                 marginals: [-5.000e-01 -5.000e-01]
 mip_node_count: 0
 mip_dual_bound: 0.0
        mip_gap: 0.0

文章来源地址https://www.toymoban.com/news/detail-698720.html

到了这里，关于数学建模--线性规划方法的Python实现的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！