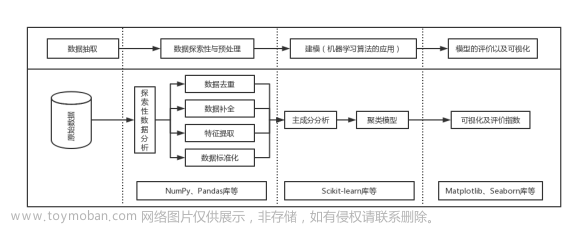
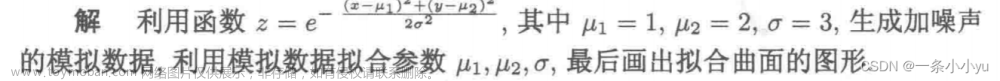数学建模圈养湖羊的空间利用率-Toy模板网

这篇具有很好参考价值的文章主要介绍了数学建模圈养湖羊的空间利用率。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

数学建模圈养湖羊的空间利用率

问题：规模化的圈养养殖场通常根据牲畜的性别和生长阶段分群饲养，适应不同种类、不同阶段的牲畜对空间的不同要求，以保障牲畜安全和健康；与此同时，也要尽量减少空间闲置所造成的资源浪费。在实际运营中，还需要考虑市场上饲料价格和产品销售价格的波动以及气候、疾病、种畜淘汰、更新等诸多复杂且关联的因素，但空间利用率是相对独立并影响养殖场经营效益的重要问题。

解题思路：
针对这个湖羊养殖场的问题，可以建立一个数学模型来优化空间利用率和生产计划。首先，我们可以考虑以下参数：

交配周期： $T_{\text{配}}$ （天）
怀孕周期： $T_{\text{孕}}$ （天）
分娩周期： $T_{\text{分}}$ （天）
哺乳周期： $T_{\text{哺}}$ （天）
育肥周期： $T_{\text{育}}$ （天）
空怀休整周期： $T_{\text{休}}$ （天）
种公羊与基础母羊的比例： $R$ （一只种公羊对应多少只基础母羊）
标准羊栏容纳的基础母羊数量： $C_{\text{基础}}$ （只）
标准羊栏容纳的种公羊数量： $C_{\text{公}}$ （只）
羊栏的使用方案： $U_i$ （不同周期的羊栏使用情况）
年化出栏羊只数量： $Y$ （只）
问题1可以通过以下方式解决：

计算每只基础母羊的产羔数量： $\frac{T_{\text{孕}}}{T_{\text{配}}} \times \frac{2}{T_{\text{孕}}} = \frac{2}{T_{\text{配}}}$
计算每只基础母羊的年化产羔数量： $\frac{365}{T_{\text{孕}}} \times \frac{2}{T_{\text{配}}}$
计算养殖场种公羊的数量： $\frac{365}{T_{\text{孕}}} \times \frac{2}{T_{\text{配}}} \times R$
计算年化出栏羊只数量： $\frac{365}{T_{\text{育}}} \times C_{\text{基础}}$
问题2可以通过线性规划等方式来解决，目标是最大化年化出栏羊只数量 $Y$ ，约束条件包括不同周期的羊栏使用情况 $U_i$ 和养殖场的容量限制。

问题3则需要引入不确定性因素，可以使用蒙特卡洛模拟等方法来考虑配种成功率、分娩羔羊数目和死亡率的不确定性，以及调整哺乳时间对空间需求的影响。

注意：思路仅供参考，它用后果自负！！

详细代码资料：https://github.com/HuaandQi/Mathematical-modeling.git

代码文章来源地址https://www.toymoban.com/news/detail-699407.html

import numpy as np
from scipy.optimize import linprog

# 目标函数的系数
c = [-365 / T_育]

# 不等式约束矩阵 A_ub * x <= b_ub
A_ub = np.array([[-365 / T_配, 0, 0, 0, 0, 0],  # 配种周期
                 [0, -365 / T_孕, 0, 0, 0, 0],  # 孕期
                 [0, 0, -365 / T_分, 0, 0, 0],  # 分娩期
                 [0, 0, 0, -365 / T_哺, 0, 0],  # 哺乳期
                 [0, 0, 0, 0, -365 / T_育, 0],  # 育肥期
                 [0, 0, 0, 0, 0, -365 / T_休]])  # 休整期

# 不等式约束右侧 b_ub
b_ub = [-365 / T_配 * 2,  # 配种周期
        -365 / T_孕 * 2,  # 孕期
        -365 / T_分,      # 分娩期
        -365 / T_哺,      # 哺乳期
        -365 / T_育,      # 育肥期
        -365 / T_休]      # 休整期

# 变量的边界
x_bounds = [(0, C_基础), (0, C_公), (0, C_基础), (0, C_基础), (0, C_基础), (0, C_基础)]

# 求解线性规划问题
res = linprog(c, A_ub=A_ub, b_ub=b_ub, bounds=x_bounds)

# 输出结果
print("最大年化出栏羊只数量：", -res.fun)
print("最优解：")
print("基础母羊数量：", res.x[0])
print("种公羊数量：", res.x[1])
print("第一周期羊栏使用数量：", res.x[2])
print("第二周期羊栏使用数量：", res.x[3])
print("第三周期羊栏使用数量：", res.x[4])
print("第四周期羊栏使用数量：", res.x[5])