链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
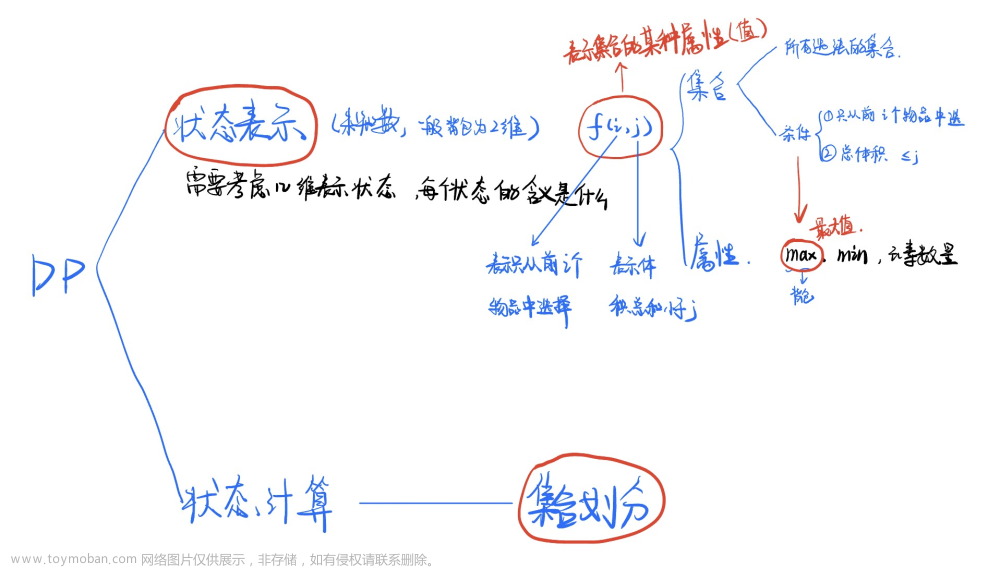
有一个箱子容量为V(正整数,0 ≤ V ≤ 20000),同时有n个物品(0<n ≤ 30),每个物品有一个体积(正整数)。
要求n个物品中,任取若干个装入箱内,使箱子的剩余空间为最小。文章来源:https://www.toymoban.com/news/detail-699451.html
分析:
不还是01背包求最大价值嘛,只是每个物体的价值与所占体积一样。文章来源地址https://www.toymoban.com/news/detail-699451.html
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
void solve()
{
ll v;
cin>>v;
ll n;
cin>>n;
ll dp[v+1];
memset(dp,0,sizeof dp);
ll a[n+1];
for(ll i=1;i<=n;i++)cin>>a[i];
for(ll i=1;i<=n;i++)
{
for(ll j=v;j>=a[i];j--)
{
dp[j]=max(dp[j],dp[j-a[i]]+a[i]);
}
}
cout<<v-dp[v]<<'\n';
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
ll t=1;
while(t--)
solve();
return 0;
}到了这里,关于01背包(换汤不换药)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!