稀疏数组
二维数组转稀疏数组的思路
-
遍历原始二维数组,得到有效数据的个数sum
-
根据sum可以创建稀疏数组
sparseArr[sum+1][3] 稀疏数组行不定 列固定3列 row col val
-
将二维数组有效数据存储到稀疏数组
稀疏数组转原始的二维数组的思路
-
先读取稀疏数组第一行,根据第一行的数据,创建原始的二维数组
-
接着再读取稀疏数组后面几行的数据,并赋给原始的二维数组即可
牢记int用throw new RuntimeException, void 用打印异常信息
类型为void时,使用return退出程序
链表
单链表
-
先创建一个头结点,作用是表示单链表的头
-
后面我们每添加一个结点,就直接加入到链表的后面
需要按照编号的顺序添加
-
首先找到新添加的节点的位置,是通过辅助变量,通过遍历来搞定
-
新的节点.next=temp.next
-
将temp.next=新的节点
链表是以节点的方式来存储,是链式存储
每个节点包含data域,next域:指向下一个节点
链表的各个节点不一定是连续存储
对于单向链表增加删除通常设置临时变量temp=head
对于双向链表删除设置临时变量temp=head.next
单向环形链表
-
先创建第一个节点,让first指向该节点,并形成环形
-
后面当我们每创建一个新的节点,就把该节点,加入到已有的环形链表中即可
遍历环形链表
-
先让一个辅助指针(变量)curBoy,指向first节点
-
然后通过一个while循环遍历该环形链表即可 curBoy.next==first结束
栈
使用栈完成表达式的计算思路
-
通过一个index值(索引),来遍历我们的表达式
-
如果我们发现是一个数字,就直接入数栈
-
如果发现扫描到是一个符号,分情况如下:
-
如果发现当前的符号栈为空,就直接入栈
-
如果符号栈中有符号,就进行比较;如果当前的符号优先级小于或等于栈中符号,就需要从数栈中pop出两个数,从符号栈中pop出一个符号,进行运算,将得到结果,入数栈,然后将当前的符号入符号栈;如果当前符号的优先级大于栈中符号,则直接入栈
-
-
当表达式扫描完毕,就顺序的从数栈和符号栈中pop出相应的数和符号,并运行
-
最后在数栈只有一个数字,就是表达式的结果
验证3+2*6-2
后缀表达式
从左至右扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的运算,并将结果入栈;重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果
正则表达式:"\\d+"代表多位数
中缀表达式转换为后缀表达式
-
初始化两个栈:运算符栈s1和储存中间结果的栈s2
-
从左到右扫描中缀表达式
-
遇到操作数时,压入s2
-
遇到运算符时,比较s1栈顶运算符的优先级
-
如果s1为空,或者s1栈顶为左括号,则直接将该运算符入栈
-
如果该运算符优先级大于s1栈顶运算符优先级,则直接将该运算符入栈
-
否则,将s1栈顶运算符弹出并压入s2栈中,再次回到步骤4起点判断
-
-
遇到括号时,
-
如果是左括号,则直接压入s1栈
-
如果是右括号,则依次弹出s1栈顶的运算符,并压入到s2栈中,直到遇到左括号为止,这对括号便不存在了
-
-
一直重复步骤2到5直到表达式结束
-
将s1中剩余的运算符依次弹出并压入s2
-
依次弹出s2中的元素并输出,结果的逆序即为后缀表达式
递归调用规则
-
当程序执行到一个方法时,就会开辟一个独立的空间(栈)
-
每个空间的数据(局部变量),是独立的
八皇后问题(7k7k小游戏)
一维数组解决问题:arr[8]={0,4,7,5,2,6,1,3}//对应arr下标 表示第几行,即第几个皇后,arr[i]=val,表示第i+1个皇后,放在第i+1行的第val+1列
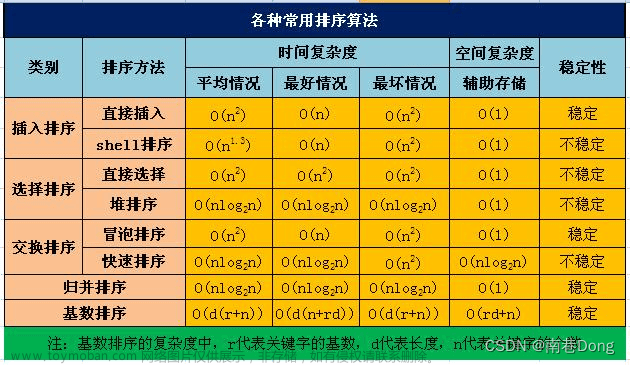
内部排序
内部排序
-
冒泡排序(比较相邻位置)稳定
-
选择排序(比较所有数)最小值 最小值索引 不稳定
-
直接插入排序 插入值 插入索引 稳定
-
希尔排序 数组长度/2=步长 比较步长之间的数 不稳定
-
快速排序 找到一个基准arr【(0+arr.length-1)/2】小于等于放在基准左边,大于等于放在基准右边 不稳定
-
归并排序 找到mid=(0+arr.length-1)/2 分解递归后接着合并 稳定
-
基数排序 稳定
-
第一轮排序
-
将每个元素的个位数取出来,然后看这个数应该放在哪个一维数组
-
按照一维数组的下标依次取出数据,放入原来数组
-
第二轮排序
-
将每个元素的十位数取出来,然后看这个数应该放在哪个一维数组
-
按照一维数组的下标依次取出数据,放入原来数组
-
第三轮排序
-
将每个元素的百位数取出来,然后看这个数应该放在哪个一维数组
-
按照一维数组的下标依次取出数据,放入原来数组
-
直到每个元素的n位数取出来都是0时即为排序后的数组
-
查找
-
顺序查找(线性查找)
-
二分查找/折半查找
-
插值查找
int mid=left+(right-left)*(findVal-arr[left])/(arr[right]-arr[left]); 注意事项, 1.对于数据量较大,关键字分布比较均匀的查找表来说,采用插值查找,速度较快 2.关键字分布不均匀的话,不一定比二分查找好
-
斐波那契查找文章来源:https://www.toymoban.com/news/detail-699888.html
文章来源地址https://www.toymoban.com/news/detail-699888.html
到了这里,关于数据结构理论知识的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!