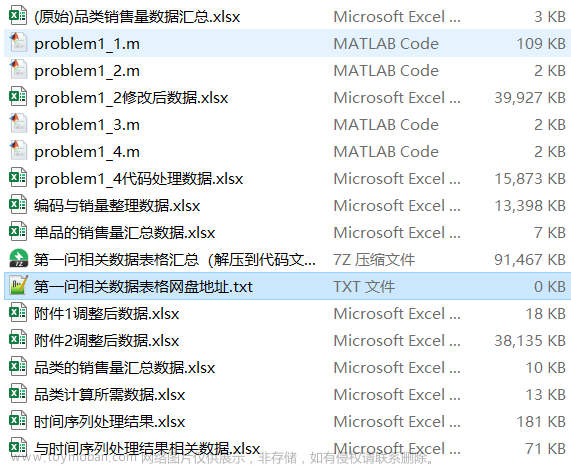
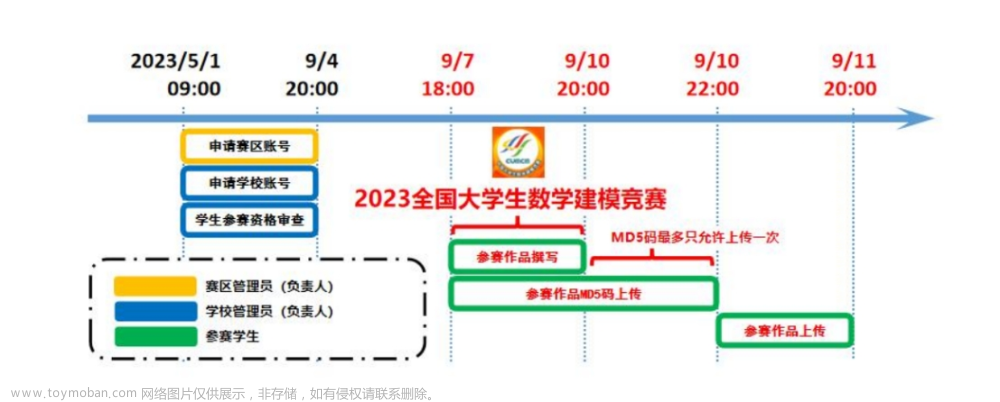
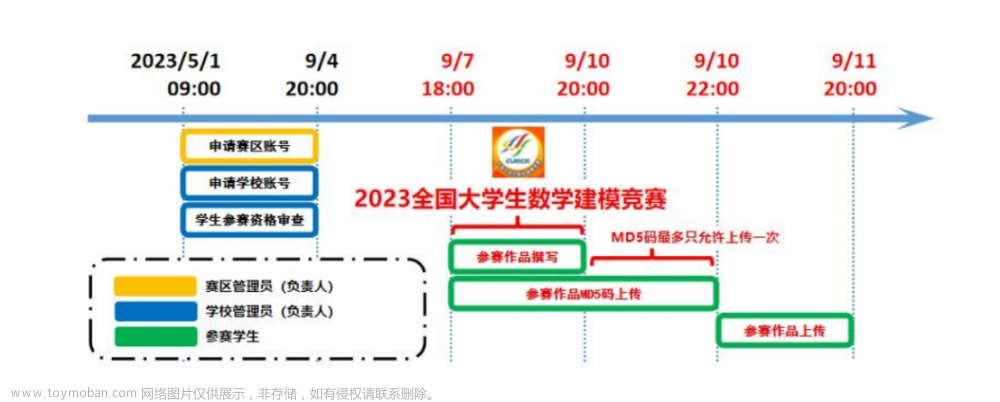
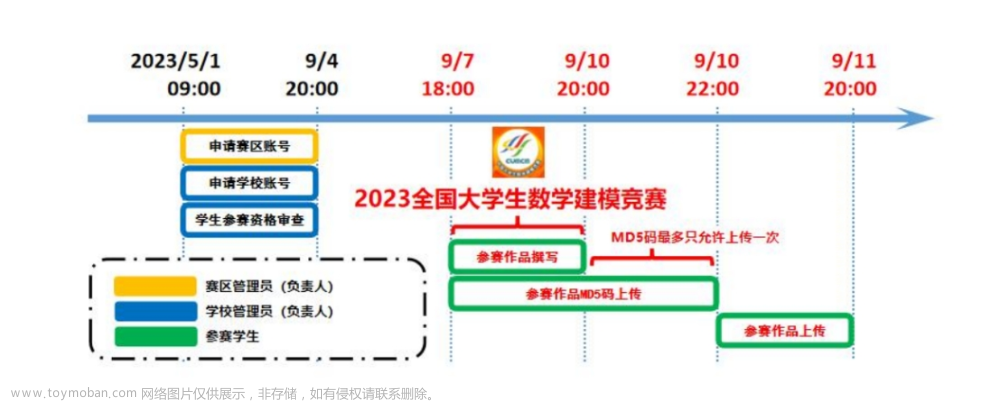
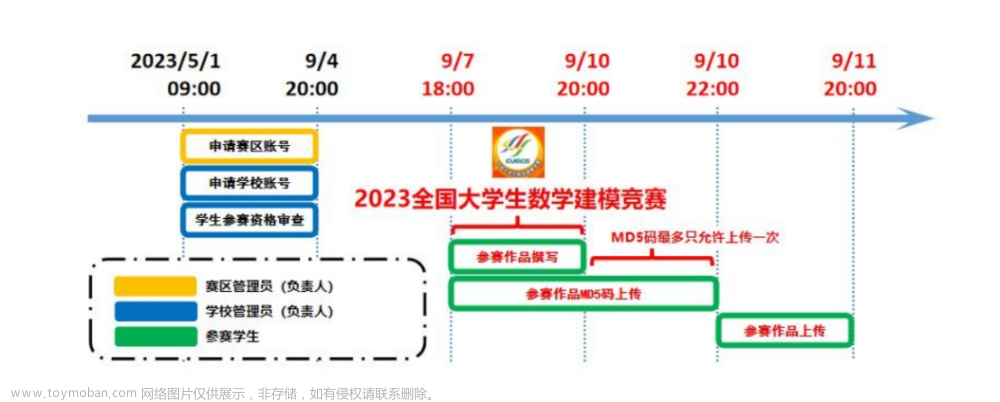
大家好呀,全国大学生数学建模竞赛今天下午开赛啦,在这里先带来初步的选题建议及思路。
目前团队正在写B题和C题完整论文,后续还会持续更新哈,以下只是比较简略的图文版讲解,团队目前正在写B、C题完整论文,后续会更新哈,详细的视频版讲解请移步:
2023数学建模国赛选题建议及B、C题初步思路_哔哩哔哩_bilibili
首先是主基调:
本次国赛建议小白队伍选择C题,典型的数据分析及优化题目。数理基础稍微好一点可以选择B题目,最难的其实只是数学公式推导,这个我们会完成,到时候直接参考我们的就行。A题目比较硬核的物理类题目,不推荐没有相关专业背景的人选择。本次团队会BC题同时进行,尽量在9.8晚更新完整论文及讲解视频。
接下来开始具体讲解:
B题:多波束测线问题
问题 1
与测线方向垂直的平面和海底坡面的交线构成一条与水平面夹角为 的斜线(图 7),称 为坡度。请建立多波束测深的覆盖宽度及相邻条带之间重叠率的数学模型。

若多波束换能器的开角为 120∘,坡度为 1.5 ∘,海域中心点处的海水深度为 70 m,利用上述模型计算表 1 中所列位置的指标值,将结果以表 1 的格式放在正文中,同时保存到 result1.xlsx 文件中。
对于第一问而言,我们首先需要根据题目的背景信息这些图片和基础的公式:

进行理论公式的具体推导:

在推导结束之后,我们采用matlab进行实际求解:

求解之后可以得到结果如下:
可以看到,已经求解除出了针对于不同距离的深度、宽度以及重叠率等数据:

第一问结束,当然,以上仅仅是我在刚刚这些时间里确定的初步的求解代码,后续完成完整论文时可能会进一步优化。
问题2:
问题 2 考虑一个矩形待测海域(图 8),测线方向与海底坡面的法向在水平面上投影的夹 角为 ,请建立多波束测深覆盖宽度的数学模型。
若多波束换能器的开角为 120∘,坡度为 1.5 ∘,海域中心点处的海水深度为 120 m,利用上 述模型计算表 2 中所列位置多波束测深的覆盖宽度,将结果以表 2 的格式放在正文中,同时保 存到 result2.xlsx 文件中。
第二问本质上就是在第一问的基础上,将二维平面的推导计算换到三维上来:

最终我们需要完成的是针对于不同测线方向夹角和测量船距海域中心点处的距离/海里 计算得出覆盖宽度。
那么依然是跟第一问一样的流程,先推导出计算宽度的理论公式,然后进行实际代码求解即可。这个等我后期更新吧。
到了三四问,就需要基于一二问的基础设计测线了,这个后面我再具体解答吧。
C题:蔬菜类商品的自动定价与补货决策
问题1:
问题 1 蔬菜类商品不同品类或不同单品之间可能存在一定的关联关系,请分析蔬菜各品类及单品销售量的分布规律及相互关系。
什么叫分布规律呢?这里我初步确定的分布规律有:
首先是品类和单品的统计规律,例如单品销量排布,品类的销量排布等,可以看出来哪个最高。
其次,还有关于时间和季节的分布规律,这里我们需要绘制时间序列图以及进行实际的季节性时间序列分析,这是因为在题目背景中已经告诉我们:

但我们怎么获取品类的具体销量数据呢?我们看一下附件2:

附件2是没有给出品类信息的,因此,我们需要将附件1中的品类数据匹配进去,这个还是比较难的,因为附件2有80多w数据,但目前我也已经完成了合并:

以上合并的数据表格我也会免费发放哈,完整数据表格的讲解可以看本文章最下面的视频。
在合并完成之后,我们就可以开始直接分类汇总计算分布以及进行时间序列分析了,这个到时候看我具体结果吧,等我更新。
对于相互关系,我们需要做相关性分析,将六个品类分为6个表格,然后汇总在一起,处理完缺失值之后,直接进行相关性分析得出具体相关性大小即可。
第一问结束
问题2:
考虑商超以品类为单位做补货计划,请分析各蔬菜品类的销售总量与成本加成定价的关系,并给出各蔬菜品类未来一周(2023 年 7 月 1-7 日)的日补货总量和定价策略, 使得商超收益最大。
依然是根据品类来,一共是6个品类:

先研究销售量和定价关系,这里我们可以先采用机器学习,直接无脑代入得出一个回归模型。
接下来为了预测补货总量,我们先预测销售量,当日销售量多少我们就补多少货,这是因为题目中以及附件中并没有给出库存量的概念。这里的预测我们可以直接采用时间序列预测。
接下来是定价策略,这一点就比较难了,因为我们需要先计算利润,基于利润最大才能给出最佳定价策略。
对于利润的计算,我们需要考虑到附件3的成本以及附件4的损耗量,这里我给出的最终优化目标是:

每一个符号说明还是看我讲解视频吧,没时间打字了。
然后进行代码实际求解:

问题3:
因蔬菜类商品的销售空间有限,商超希望进一步制定单品的补货计划,要求可 售单品总数控制在 27-33 个,且各单品订购量满足最小陈列量 2.5 千克的要求。根据 2023 年 6 月 24-30 日的可售品种,给出 7 月 1 日的单品补货量和定价策略,在尽量满足市场对各 品类蔬菜商品需求的前提下,使得商超收益最大。
这里本质上就是不分析品类了,但也不需要分析那么多细类,我们只需要在限制条件下分析27-33个单品即可。依然是给出优化目标和函数然后实际求解即可,后期等我实际更新吧。文章来源:https://www.toymoban.com/news/detail-699922.html
以上免费数据表格、代码以及后续完整完整成品领取可以看下方我的个人卡片哈↓:文章来源地址https://www.toymoban.com/news/detail-699922.html
到了这里,关于2023数学建模国赛选题建议及BC题思路的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!