定义
蒙特卡罗方法又称统计模拟法、随机抽样技术,是一种随机模拟方法,以概率和统计理论方法为基础的一种计算方法,是使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系,用电子计算机实现统计模拟或抽样,以获得问题的近似解。为象征性地表明这一方法的概率统计特征,故借用赌城蒙特卡罗命名。
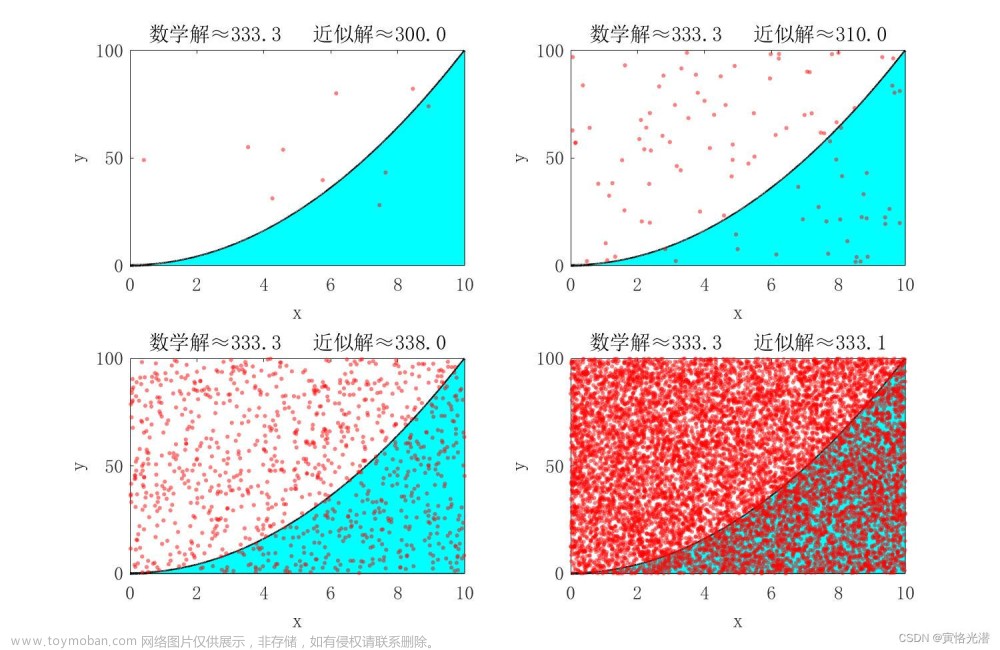
通俗的讲,就是通过 生成大量随机数 进行模拟 得最优解(近似最优解)的方法。
原理
由大数定理可知,当样本容量足够大时,事件的发生频率即为其概率。
注:蒙特卡罗模拟不是一种算法。准确的来说只是⼀种思想,或者是一种方法。
应用示例(附MatLab代码)
应用一:估计自然对数的底数 e 的值
类似布丰用投针实验估计了 π 值,一群人每人写一张卡片,卡片上是自己的名字。把卡片收上去,打乱次序,再随机地发给每一个人。每个人拿到的都不是自己卡片的概率趋近于1/e,多做几次这个实验,用频率代替概率,求倒数,就可以了。
MatLab代码示例
clear;clc
tic %计算tic和toc中间部分的代码的运行时间
n = 100; % 总人数
N = 10000000; % 循环的次数
unequal = 0; % 每个人收到的卡片都不是自己的
for i = 1:N % 循环N次
X = randperm(n); % 生成新的随机数序列,模拟给每个人发卡片
judge = 0; % judge = 0,则每个人收到的卡片都不是自己的
for j = 1:n
if X(j) == j
judge = 1; % 如果存在有人收到的卡片是自己的,便记judge为1,跳出循环
break;
end
end
if judge == 0
unequal = unequal + 1;
end
end
e_1 = unequal / N; % 每个人拿到的都不是自己卡片的概率为1/e
e = e_1^-1; % 取倒数求e
disp(['蒙特卡罗估计的自然常数e的值为',num2str(e)]); % 打印e的值(自然常数真实值约为2.7182)
toc %计算tic和toc中间部分的代码的运行时间
输出结果
蒙特卡罗估计的自然常数e的值为2.7188
时间已过 54.929325 秒。
简化版本的代码
clear;clc
tic %计算tic和toc中间部分的代码的运行时间
n = 100; % 总人数
N = 10000000; % 循环的次数
unequal = 0; % 每个人收到的卡片都不是自己的
for i = 1:N % 循环N次
X = randperm(n); % 生成新的随机数序列,模拟给每个人发卡片
if isempty(find(X == [1:n])) % 直接将新的随机数序列与1-n的顺序数列作比较
% find(X)可以用来返回这个向量中非零元素的下标,如果X中所有元素都为0,则返回空值
% isempty(X)函数可以用来判断X是否为空, 如果X为空, isempty(X) 返回逻辑值1(true),否则返回逻辑值0(false)。
unequal = unequal + 1;
end
end
e_1 = unequal / N; % 每个人拿到的都不是自己卡片的概率为1/e
e = e_1^-1; % 取倒数求e
disp(['蒙特卡罗估计的自然常数e的值为',num2str(e)]); % 打印e的值(自然常数真实值约为2.7182)
toc %计算tic和toc中间部分的代码的运行时间
输出结果
蒙特卡罗估计的自然常数e的值为2.718
时间已过 60.641203 秒。
可以看到使用蒙特卡罗估计出的自然常数e的值基本接近其实际值。
如果你想知道本题具体的数学推导过程,可见知乎 - 布丰用投针实验估计了 π 值,那么用什么简单方法可以估计自然对数的底数 e 的值?文章来源:https://www.toymoban.com/news/detail-700098.html
应用二:求解非线性规划问题
 文章来源地址https://www.toymoban.com/news/detail-700098.html
文章来源地址https://www.toymoban.com/news/detail-700098.html
(1)MatLab代码——初次寻找最小值
clc,clear;
format long g %可以将Matlab的计算结果显示为一般的长数字格式(默认会保留四位小数,或使用科学计数法)
tic %计算tic和toc中间部分的代码的运行时间
n = 10000000; % 生成的随机数的组数
x1 = unifrnd(0,16,n,1); % 生成在[0,16]之间均匀分布的随机数组成的n行1列的向量构成x1
x2 = unifrnd(0,8,n,1); % 生成在[0,8]之间均匀分布的随机数组成的n行1列的向量构成x2
fmin = inf; % 初始化 fmin = 正无穷
X = zeros(1,2); % 初始化储存最小处x1, x2值的数组
for i = 1:n
x = [x1(i), x2(i)];
if( x(1)+2*x(2) < 16 & x(1)+2*x(2) < 16 )
r = 2*(x(1)^2)+x(2)^2-x(1)*x(2)-8*x(1)-3*x(2);
if(r < fmin)
fmin = r;
X = x;
end
end
end
disp(['f(x)最小值为:', num2str(fmin)]); % 注意:此处原本的字符串不能用双引号。
disp('最小处x1, x2值为:');
disp(X);
toc %计算tic和toc中间部分的代码的运行时间
输出结果
f(x)最小值为:-15.1429
x1, x2值为
2.71485111081151 2.85830659834113
时间已过 1.780016 秒。
(2)MatLab代码——缩小范围重新模拟得到更加精确的取值
clc,clear;
format long g %可以将Matlab的计算结果显示为一般的长数字格式(默认会保留四位小数,或使用科学计数法)
tic %计算tic和toc中间部分的代码的运行时间
n = 10000000; % 生成的随机数组数
x1 = unifrnd(2.5,3,n,1); % 生成在[2.5,3]之间均匀分布的随机数组成的n行1列的向量构成x1
x2 = unifrnd(2.5,3,n,1);% 生成在[2.5,3]之间均匀分布的随机数组成的n行1列的向量构成x2
fmin = inf; % 初始化 fmin = 正无穷
X = zeros(1,2); % 初始化储存最小处x1, x2值的数组
for i = 1:n
x = [x1(i), x2(i)]; % 构造x向量,储存第i个x1,x2对应值。
if(x(1)+2*x(2) < 16 & x(1)+2*x(2) < 16)
r = 2*(x(1)^2)+x(2)^2-x(1)*x(2)-8*x(1)-3*x(2);
if(r < fmin)
fmin = r;
X = x;
end
end
end
disp(['f(x)最小值为:', num2str(fmin)]); % 注:此处原本的字符串不能用双引号。
disp('最小处x1, x2值为:');
disp(X);
toc %计算tic和toc中间部分的代码的运行时间
输出结果
f(x)最小值为:-15.1429
x1, x2值为
2.71423617782718 2.85717715949967
时间已过 1.758372 秒。
到了这里,关于蒙特卡罗(洛)模拟——手把手教你数学建模的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!