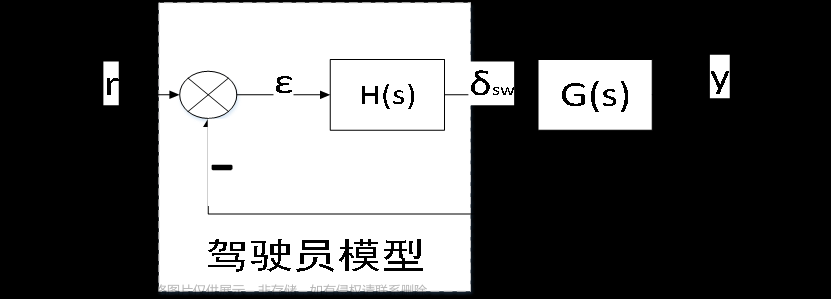
建立道路-车辆误差模型
首先要建立车辆质心相对于车道中心线的误差模型,示意图如下所示:
Frenet坐标系与全局笛卡尔Cartesian坐标系转换
- 参考:https://mp.weixin.qq.com/s/VrbvIdoqFu6EBFZOwdaKUA 自动驾驶规控混乱源头:Frenet坐标系
Cartesian转Frenet公式
在 C a r t e s i a n Cartesian Cartesian坐标系下,车辆运动状态可以描述为 ( x , y , θ , v , a , k ) (x, y, \theta, v, a, k) (x,y,θ,v,a,k), 在 F r e n e t Frenet Frenet坐标系下, 车辆的运动状态可以描述为 ( s r , x r , y r , θ r , k r , k r ′ ) (s_r, x_r, y_r,\theta_r, k_r, k_r') (sr,xr,yr,θr,kr,kr′),求车辆在Frenet坐标系下的运动状态表达: [ s , s ˙ , s ¨ , d , d ˙ , d ¨ , d ′ , d ′ ′ ] \left[s, \dot{s}, \ddot{s}, d, \dot{d}, \ddot{d}, d', d''\right] [s,s˙,s¨,d,d˙,d¨,d′,d′′]
公式总结如下:
s
=
s
r
s=s_r
s=sr
s ˙ = v ∗ cos ( θ − θ r ) 1 − k r ∗ d \dot{s} =\frac{v*\cos(\theta -\theta_r)}{1-k_r*d} s˙=1−kr∗dv∗cos(θ−θr)
s ¨ = a ∗ cos ( θ − θ r ) − s ˙ 2 ∗ [ d ′ ( k ∗ 1 − k r cos ( θ − θ r ) − k r ) − ( k r ′ ∗ d + k r ∗ d ′ ) ] 1 − k r ∗ d \ddot{s}=\frac{a*\cos(\theta -\theta_r)-\dot{s}^2*[d'(k*\frac{1-k_r}{\cos(\theta -\theta_r)}-k_r)-(k_r'*d+k_r*d')]}{1-k_r*d} s¨=1−kr∗da∗cos(θ−θr)−s˙2∗[d′(k∗cos(θ−θr)1−kr−kr)−(kr′∗d+kr∗d′)]
d = − sin θ r ∗ ( x − x r ) + cos θ r ∗ ( y − y r ) d=-\sin \theta_r*(x-x_r)+\cos \theta_r*(y-y_r) d=−sinθr∗(x−xr)+cosθr∗(y−yr)
d ˙ = v ∗ sin ( θ − θ r ) \dot{d}=v*\sin(\theta-\theta_r) d˙=v∗sin(θ−θr)
d ¨ = a ∗ sin ( θ − θ r ) \ddot{d}=a*\sin(\theta-\theta_r) d¨=a∗sin(θ−θr)
d ′ = ( 1 − k r ∗ d ) tan ( θ − θ r ) d'=(1-k_r*d) \tan(\theta-\theta_r) d′=(1−kr∗d)tan(θ−θr)
d ′ ′ = − ( k r ′ + k r ∗ d ′ ) tan ( θ − θ r ) + 1 − k r ∗ d cos 2 ( θ − θ r ) ∗ ( k ∗ 1 − k r ∗ d cos ( θ − θ r ) − k r ) d''=-(k_r'+k_r*d') \tan(\theta-\theta_r) +\frac{1-k_r*d}{\cos^2(\theta-\theta_r)}*(k* \frac{1-k_r*d}{\cos(\theta-\theta_r)} - k_r) d′′=−(kr′+kr∗d′)tan(θ−θr)+cos2(θ−θr)1−kr∗d∗(k∗cos(θ−θr)1−kr∗d−kr)
其中:
C a r t e s i a n Cartesian Cartesian坐标系下的量:
- x , y x,y x,y表示车辆在 C a r t e s i a n Cartesian Cartesian坐标系下的位置信息;
- θ \theta θ为车辆在 C a r t e s i a n Cartesian Cartesian坐标系下的航向角;
- k k k为 C a r t e s i a n Cartesian Cartesian坐标系下的曲率;
- v v v为车辆在 C a r t e s i a n Cartesian Cartesian坐标系下的线速度;
- a = d v d t a=\frac{dv}{dt} a=dtdv为车辆在 C a r t e s i a n Cartesian Cartesian坐标系下的加速度;
F r e n e t Frenet Frenet坐标系下的量:
- s s s为 F r e n e t Frenet Frenet坐标系下的纵向位移;
- s ˙ = d s d t \dot{s}=\frac{ds}{dt} s˙=dtds为 F r e n e t Frenet Frenet坐标系下纵向速度;
- s ¨ = d s ˙ d t \ddot{s}=\frac{d \dot{s}}{dt} s¨=dtds˙为 F r e n e t Frenet Frenet坐标系下纵向加速度;
- d d d为横向位移, 即 F r e n e t Frenet Frenet坐标系下横坐标;
- d ˙ \dot{d} d˙为为 F r e n e t Frenet Frenet坐标系下的横向速度;
- d ¨ \ddot{d} d¨为为 F r e n e t Frenet Frenet坐标系下的横向加速度;
- d ′ = d d d s d'= \frac{d d}{ds} d′=dsdd为 F r e n e t Frenet Frenet坐标系下横向位移对纵向坐标的一阶导数;
- d ′ ′ = d d ′ d s d''= \frac{d d'}{ds} d′′=dsdd′为 F r e n e t Frenet Frenet坐标系下横向位移对纵向坐标的二阶导数;
- 注: x ˙ = d x d t , x ′ = d x d s \dot{x}=\frac{dx}{dt},x'=\frac{dx}{ds} x˙=dtdx,x′=dsdx
计算横向误差
在使用Frenet坐标系时,首先根据车辆位置找到参考路径上距离车辆最近的点(匹配点match_point),以匹配点为参考路径点并建立s-d坐标系,如上图所示。 首先计算车辆相对位置:
d
x
=
x
−
x
m
a
t
c
h
d
y
=
y
−
y
m
a
t
c
h
dx=x-x_{match} \\ dy=y-y_{match}
dx=x−xmatchdy=y−ymatch
通过二维坐标系旋转公式可以得到车辆在frenet坐标系中相对于道路中心线的相对坐标为:
[
s
d
]
=
[
cos
ψ
m
a
t
c
h
sin
ψ
m
a
t
c
h
−
sin
ψ
m
a
t
c
h
cos
ψ
m
a
t
c
h
]
[
d
x
d
y
]
\begin{bmatrix} s \\d \end{bmatrix} =\begin{bmatrix} \cos \psi_{match} & \sin \psi_{match} \\ -\sin \psi_{match} & \cos \psi_{match} \end{bmatrix} \begin{bmatrix} dx \\ dy \end{bmatrix}
[sd]=[cosψmatch−sinψmatchsinψmatchcosψmatch][dxdy]
定义:
e
1
e_1
e1为横向误差,
e
2
e_2
e2为航向角误差、
e
1
˙
\dot{e_1}
e1˙为横向误差变化速率、
e
2
˙
\dot{e_2}
e2˙为航向角误差变化率,则有:
e
1
=
−
sin
ψ
m
a
t
c
h
∗
d
x
+
cos
ψ
m
a
t
c
h
∗
d
y
e
2
=
ψ
−
ψ
m
a
t
c
h
\begin{aligned} e_1 & =-\sin \psi_{match}*dx+\cos \psi_{match}*dy \\ e_2 & =\psi-\psi_{match} \end{aligned}
e1e2=−sinψmatch∗dx+cosψmatch∗dy=ψ−ψmatch
其中:
ψ
\psi
ψ车辆当前位置航向角,
ψ
m
a
t
c
h
\psi_{match}
ψmatch为路径参考点的航向角,进一步有:
e
1
˙
=
v
∗
sin
(
ψ
−
ψ
m
a
t
c
h
)
e
2
˙
=
ψ
˙
−
ψ
m
a
t
c
h
˙
=
ψ
˙
−
v
∗
k
m
a
t
c
h
\begin{aligned} \dot{e_1} & =v*\sin(\psi-\psi_{match}) \\ \dot{e_2} & =\dot{\psi}-\dot{\psi_{match}}=\dot{\psi}-v*k_{match} \end{aligned}
e1˙e2˙=v∗sin(ψ−ψmatch)=ψ˙−ψmatch˙=ψ˙−v∗kmatch
其中:
v
v
v为车辆当前纵向速度,
ψ
˙
\dot{\psi}
ψ˙为车辆当前横摆角速度(或航向角变化率),
k
m
a
t
c
h
k_{match}
kmatch为匹配点曲率。
计算纵向误差
在纵向控制中,涉及到起始点、匹配点、参考点、预瞄点,示意图如下:

Frenet坐标系定义
s s s:沿参考轨迹纵向累积距离
s ˙ \dot{s} s˙:沿参考轨迹纵向速度
d d d:参考轨迹横向距离
d ˙ \dot{d} d˙:参考轨迹横向速度
关键路径点
Apollo规划模块计算的参考轨迹具有一个全局时间戳,表示参考轨迹起始点的时间戳。参考轨迹上的其他点采用相对时间戳表示,即相对于起始点的时间戳。
(1)起始点:参考轨迹的起始点,相对时间戳为0s;
(2)匹配点 ( x m a t c h , y m a t c h ) (x_{match},y_{match}) (xmatch,ymatch):根据车辆位置找到参考路径最近点,并以此点建立Frenet坐标系。由位置寻找,与相对时间戳无关;
// 找到距离车辆位置最近的参考路径点
// 匹配最近点时:插值法+优选法(黄金分割法)来找到最近的点
auto matched_point = trajectory_analyzer->QueryMatchedPathPoint(
vehicle_state->x(), vehicle_state->y());
// 根据匹配点建立Frenet坐标系,并计算横/纵向坐标
trajectory_analyzer->ToTrajectoryFrame(
vehicle_state->x(), vehicle_state->y(), vehicle_state->heading(),
vehicle_state->linear_velocity(), matched_point, &s_matched,
&s_dot_matched, &d_matched, &d_dot_matched);
以匹配点作为参考点,建立Frenet坐标系,车辆质心在Frenet坐标系下与道路中心线相对坐标可表示为:
[
s
d
]
=
[
cos
ψ
m
a
t
c
h
sin
ψ
m
a
t
c
h
−
sin
ψ
m
a
t
c
h
cos
ψ
m
a
t
c
h
]
[
d
x
d
y
]
\begin{bmatrix} s \\ d \end{bmatrix} =\begin{bmatrix} \cos \psi_{match} & \sin \psi_{match} \\ -\sin \psi_{match} & \cos \psi_{match} \end{bmatrix} \begin{bmatrix} dx \\ dy \end{bmatrix}
[sd]=[cosψmatch−sinψmatchsinψmatchcosψmatch][dxdy]
车辆的全局坐标需考虑匹配点的纵向里程距离
s
m
a
t
c
h
s_{match}
smatch,故:
s
=
cos
ψ
m
a
t
c
h
∗
d
x
+
sin
ψ
m
a
t
c
h
∗
d
y
+
s
m
a
t
c
h
d
=
−
sin
ψ
m
a
t
c
h
∗
d
x
+
cos
ψ
m
a
t
c
h
∗
d
y
\begin{aligned} s & =\cos \psi_{match}*dx +\sin \psi_{match} * dy + s_{match} \\ d & =-\sin \psi_{match}*dx+\cos \psi_{match}*dy \end{aligned}
sd=cosψmatch∗dx+sinψmatch∗dy+smatch=−sinψmatch∗dx+cosψmatch∗dy
在Frenet坐标系下车辆的纵向速度和横向速度如下:
s
˙
=
v
∗
cos
(
ψ
−
ψ
m
a
t
c
h
)
1
−
k
m
a
t
c
h
∗
d
d
˙
=
v
∗
sin
(
ψ
−
ψ
m
a
t
c
h
)
\begin{aligned} \dot{s} & =\frac{v*\cos(\psi -\psi_{match})}{1-k_{match}*d} \\ \dot{d} & = v*\sin(\psi-\psi_{match}) \end{aligned}
s˙d˙=1−kmatch∗dv∗cos(ψ−ψmatch)=v∗sin(ψ−ψmatch)
3)参考点 ( x r e f , y r e f ) (x_{ref},y_{ref}) (xref,yref):根据当前绝对时间戳确定参考点位置;
double preview_time = lon_controller_conf.preview_window() * ts;
// 当前时间确定参考点,预瞄时间确定预瞄点
// 预瞄时间 = 预瞄窗口数目 * 预瞄窗口时间 (此例为 20 * 0.01 = 0.2s)
double current_control_time = ::apollo::cyber::Clock::NowInSeconds();
double preview_control_time = current_control_time + preview_time;
// 根据绝对时间戳匹配参考点和预瞄点
TrajectoryPoint reference_point =
trajectory_analyzer->QueryNearestPointByAbsoluteTime(
current_control_time);
TrajectoryPoint preview_point =
trajectory_analyzer->QueryNearestPointByAbsoluteTime(
preview_control_time);
// header_time_为参考轨迹的全局时间戳
// 相对路径时间戳 = 绝对时间戳 - 参考轨迹全局时间戳
// 最后根据相对路径时间戳找到参考轨迹对应点
TrajectoryPoint TrajectoryAnalyzer::QueryNearestPointByAbsoluteTime(
const double t) const {
return QueryNearestPointByRelativeTime(t - header_time_);
}
(4)预瞄点 ( x p r e , y p r e ) (x_{pre},y_{pre}) (xpre,ypre):根据预瞄绝对时间戳确定预瞄点位置,预瞄绝对时间戳=参考绝对时间戳+预瞄时间。
因此:
-
根据参考点计算出来的位置误差、速度误差以及加速度误差表达式为:
r e f S t a t i o n e r r o r = s r e f − s r e f S p e e d e r r o r = v r e f − s ˙ r e f A c c e l e r a t i o n e r r o r = a r e f − s ¨ refStation_{error}=s_{ref}-s \\ refSpeed_{error}=v_{ref}-\dot{s} \\ refAcceleration_{error}=a_{ref}-\ddot{s} refStationerror=sref−srefSpeederror=vref−s˙refAccelerationerror=aref−s¨文章来源:https://www.toymoban.com/news/detail-700161.html -
根据预瞄点计算出来的位置误差、速度误差以及加速度误差表达式为:
p r e S t a t i o n e r r o r = s r e f − s p r e S p e e d e r r o r = v r e f − s ˙ p r e A c c e l e r a t i o n e r r o r = a p r e − s ¨ preStation_{error}=s_{ref}-s \\ preSpeed_{error}=v_{ref}-\dot{s} \\ preAcceleration_{error}=a_{pre}-\ddot{s} preStationerror=sref−spreSpeederror=vref−s˙preAccelerationerror=apre−s¨文章来源地址https://www.toymoban.com/news/detail-700161.html
到了这里,关于自动驾驶控制算法——横纵向误差计算的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!