【力扣】343. 整数拆分＜动态规划、数学＞-Toy模板网

这篇具有很好参考价值的文章主要介绍了【力扣】343. 整数拆分＜动态规划、数学＞。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

【力扣】343. 整数拆分

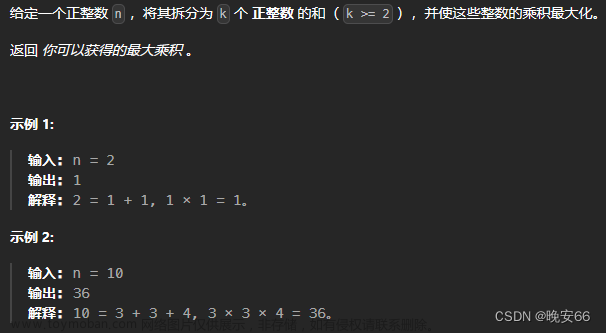
给定一个正整数 n ，将其拆分为 k 个正整数的和（ k >= 2 ），并使这些整数的乘积最大化。返回可以获得的最大乘积。

示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

提示:
2 <= n <= 58

题解

动态规划

确定 dp 数组以及下标的含义
dp[i]：分拆数字 i，可以得到的最大乘积为 dp[i]。
确定递推公式
有两种渠道得到 dp[i].
一个是 j * (i - j) 直接相乘。(2个)
一个是 j * dp[i - j]，相当于是拆分 (i - j) （3个及3个以上）
递推公式：dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
dp 数组如何初始化
dp[0]，dp[1] 就不应该初始化，也就是没有意义的数值。
dp[2] = 1
确定遍历顺序
dp[i] 是依靠 dp[i - j] 的状态，所以遍历 i 一定是从前向后遍历，先有 dp[i - j] 再有dp[i]

for (int i = 3; i <= n ; i++) {
	// 从1开始的。从0开始的话，那么让拆分一个数拆个0，求最大乘积就没有意义
    for (int j = 1; j < i - 1; j++) {
        dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
    }
}

优化：文章来源地址https://www.toymoban.com/news/detail-700487.html

for (int i = 3; i <= n ; i++) {
    for (int j = 1; j <= i / 2; j++) {
        dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
    }
}

举例推导 dp 数组（打印 dp 数组）

 public static int integerBreak(int n) {
     //dp[i] 为正整数 i 拆分后的结果的最大乘积
     int[] dp = new int[n+1];
     dp[2] = 1;
     for(int i = 3; i <= n; i++) {
         for(int j = 1; j <= i-j; j++) {
             // 这里的 j 其实最大值为 i-j,再大只不过是重复而已，
             //并且，在本题中，我们分析 dp[0], dp[1]都是无意义的，
             //j 最大到 i-j,就不会用到 dp[0]与dp[1]
             dp[i] = Math.max(dp[i], Math.max(j*(i-j), j*dp[i-j]));
             // j * (i - j) 是单纯的把整数 i 拆分为两个数 也就是 i,i-j ，再相乘
             //而j * dp[i - j]是将 i 拆分成两个以及两个以上的个数,再相乘。
         }
     }
     return dp[n];
 }

数学

public static int integerBreak2(int n) {
    if (n <= 3) {
        return n - 1;
    }
    int quotient = n / 3;
    int remainder = n % 3;
    if (remainder == 0) {
        return (int) Math.pow(3, quotient);
    } else if (remainder == 1) {
        return (int) Math.pow(3, quotient - 1) * 4;
    } else {
        return (int) Math.pow(3, quotient) * 2;
    }
}