已经写出国赛E题黄河水沙监测数据分析完整代码分析+处理结果+思路分析(30+页),包括数据预处理、数据可视化(分组数据分布图可视化、相关系数热力图可视化、散点图可视化)、回归模型(决策树回归模型、随机森林回归、GBDT回归、支持向量机回归、全连接神经网络),后续持续更新。
完整代码+结果+思路文档下载地址见文末


E题 黄河水沙监测数据分析.... 2
问题1 分析与研究.... 3
目标1: 含沙量与时间、水位、水流量的关系.... 3
目标2: 并估算近6年该水文站的年总水流量和年总排沙量.... 3
第一步:结合问题1的目标,对数据进行与处理操作.... 3
第二步:数据可视化分析,查看数据之间的关系.... 4
分组数据分布图可视化.... 6
相关系数热力图可视化.... 12
散点图可视化.... 14
目标1:解决方案,建立回归模型,分析他们之间的关系,预测含沙量.... 23
模型1:决策树回归模型.... 24
模型2:随机森林回归.... 27
模型3: GBDT回归.... 29
模型4:支持向量机回归.... 29
模型5:全连接神经网络.... 30
问题2:解决方案,(估算近6年该水文站的年总水流量和年总排沙量)31

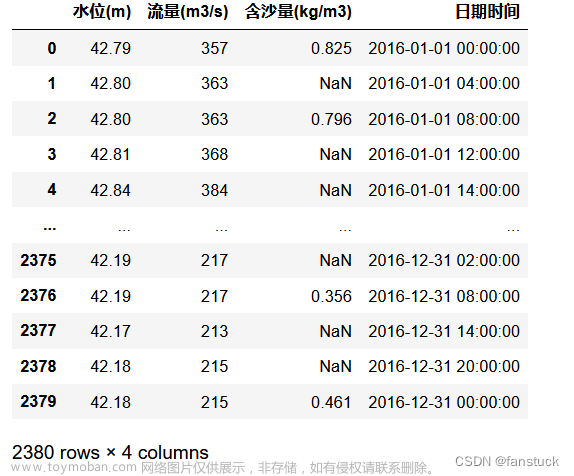
国赛E题数学建模题目如下:黄河是中华民族的母亲河。研究黄河水沙通量的变化规律对沿黄流域的环境治理、气候变化和人民生活的影响,以及对优化黄河流域水资源分配、协调人地关系、调水调沙、防洪减灾等方面都具有重要的理论指导意义。
附件1给出了位于小浪底水库下游黄河某水文站近 6年的水位、水流量与含沙量的实际监测数据,附件 2给出了该水文站近 6年黄河断面的测量数据,附件 3给出了该水文站部分监测点的相关数据。请建立数学模型研究以下问题:
问题1 研究该水文站黄河水的含沙量与时间、水位、水流量的关系,并估算近 6年该水文站的年总水流量和年总排沙量。
问题2 分析近 6年该水文站水沙通量的突变性、季节性和周期性等特性,研究水沙通量的变化规律。
问题3 根据该水文站水沙通量的变化规律, 预测分析该水文站未来两年水沙通量的变化趋势 ,并 为该水文站制订未来两年最优的采样监测方案(采样监测次数和具体时间等),使其既能及时掌握水沙通量的动态变化情况,又能最大程度地减少监测成本资源。
问题4 根据该水文站的水沙通量和河底高程的变化情况,分析每年 6 7月小浪底水库进行“调水调沙”的实际效果。如果不进行“调水调沙”, 10年以后该水文站的河底高程会如何?
问题分析
问题1 研究该水文站黄河水的含沙量与时间、水位、水流量的关系,并估算近 6年该水文站的年总水流量和年总排沙量。(完整文档和代码见文末地址)
首先导入相关库:
## 设置图像显示情况
%config InlineBackend.figure_format = "retina"
%matplotlib inline
import seaborn as sns ## 设置中文字体显示
sns.set(font= "SimSun",style="whitegrid",font_scale=1.4)
import matplotlib ## 解决坐标轴的负号显示问题
matplotlib.rcParams['axes.unicode_minus']=False
## 导入需要的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import missingno as msno
from scipy import stats
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.stats.multicomp import pairwise_tukeyhsd
import plotly.express as px
## 忽略提醒
import warnings
warnings.filterwarnings("ignore")问题1 分析与研究
2023国赛数学建模E题问题1分析如下
首先是目标1: 含沙量与时间、水位、水流量的关系
子问题:含沙量与时间的关系、含沙量与水位的关系、含沙量与水流量的关系(注意,可以分别分析两者之间的关系建模,也可以分析一个和多个变量之间关系的建模)
分析方式和步骤可以是:(1)数据清洗与整理,得到感兴趣的数据,利用可视化辅助分析之间的关系,利用相关性分析、回归分析等模型,建立数据之间的定量关系。(完整文档和代码见文末地址)
接着是目标2: 并估算近6年该水文站的年总水流量和年总排沙量
子问题:总排沙量理论上可以通过水流量和含沙量计算得到。因此重点还是分析年总水流量与含沙量之间的情况。
分析方式和步骤可以是:(1)数据清洗与整理,得到感兴趣的数据,利用可视化辅助分析之间的关系,通过相应的计算,获取目标数据。
第一步:结合问题1的目标,对数据进行与处理操作
结合附件1中给出的数据特点,我们将提供的的数据量计精确到以天为单位的精度。
第二步:数据可视化分析,查看数据之间的关系
## 根据时间变量变化的数据散点图可视化
## 水位的变化情况
plt.figure(figsize=(12,3))
p = sns.lineplot(data=dfq1, x="日期", y="水位",lw = 2)
plt.xlabel("时间")
plt.ylabel("水位(m)")
plt.title("")
plt.savefig('figs/水位的变化情况.png', dpi=300, bbox_inches='tight')
plt.show()
## 流量的变化情况
plt.figure(figsize=(12,3))
p = sns.lineplot(data=dfq1, x="日期", y="流量",lw = 2)
plt.xlabel("时间")
plt.ylabel("流量("+"$m^3$"+"/s)")
plt.title("")
plt.savefig('figs/流量的变化情况.png', dpi=300, bbox_inches='tight')
plt.show()
## 含沙量的变化情况
plt.figure(figsize=(12,3))
p = sns.lineplot(data=dfq1, x="日期", y="含沙量",lw = 2)
plt.xlabel("时间")
plt.ylabel("含沙量(kg/"+"$m^3$"+")")
plt.title("")
plt.savefig('figs/含沙量的变化情况.png',dpi=300,bbox_inches='tight')
plt.show()
## 可以发现在含沙量等特征的变化情况

分组数据分布图可视化
针对含沙量数据,进一步的分析其随时间年份上的变化趋势
sns.swarmplot(data=dfq1, x="年", y="含沙量", hue="年")
plt.xlabel("年")
plt.ylabel("含沙量(kg/"+"$m^3$"+")")
plt.title("")
plt.savefig('figs/含沙量数据随时间年份上的变化趋势.png', dpi=300, bbox_inches='tight')
plt.show()
## 可以发现2018-2021年,含沙量普遍偏高
## 针对含沙量数据,进一步的分析其随时间月份上的变化趋势
plt.figure(figsize=(12,6))
sns.swarmplot(data=dfq1, x="月", y="含沙量", hue="月")
plt.xlabel("月")
plt.ylabel("含沙量(kg/"+"$m^3$"+")")
plt.title("")
plt.savefig('figs/含沙量数据随时间月份上的变化趋势.png', dpi=300, bbox_inches='tight')
plt.show()

从可视化图像,可以发现含沙量明显的受到年、月两个变量的影响,即受到时间的影响(完整代码见文末地址)
相关系数热力图可视化
(完整代码见文末地址)
Index(['年', '月', '日', '水位', '流量', '含沙量', '日期'], dtype='object')
## 可以计算几个特征之间的相关系数,从而展示相关性的大小
## 也可以特征之间的秩相关系数
corrdf = dfq1[["年","月","日","水位","流量","含沙量"]]
corrdfval = corrdf.corr(method = "pearson")
print(corrdfval)
## 可视化相关系数热力图
plt.figure(figsize=(10,8))
ax = sns.heatmap(corrdfval,square=True,annot=True,fmt = ".2f",
linewidths=.5,cmap="YlGnBu",
cbar_kws={"fraction":0.046, "pad":0.03})
ax.set_title("相关性(pearson)")
plt.savefig('figs/相关系数热力图.png', dpi=300, bbox_inches='tight')
plt.show()
可以发现, 含沙量与日无关,月年和月是弱相关性,与水位、流量的相关性较强(这里分析的是线性关系)

散点图可视化
2023数学建模国赛E题:可视化水位与含沙量之间的散点图
(完整代码见文末地址)
plt.figure(figsize=(12,6))
sns.scatterplot(data=dfq1,x="水位", y="含沙量",
palette="Set1",s = 60)
plt.xlabel("水位(m)")
plt.ylabel("含沙量(kg/"+"$m^3$"+")")
plt.title("")
plt.savefig('figs/水位与含沙量之间的散点图1.png', dpi=300, bbox_inches='tight')
plt.show()
## 可视化 水位月含沙量之间的散点图
# plt.figure(figsize=(12,6))
sns.lmplot(data=dfq1,x="水位", y="含沙量",
palette="Set1",height=6,aspect=1.5)
plt.xlabel("水位(m)")
plt.ylabel("含沙量(kg/"+"$m^3$"+")")
plt.title("")
plt.savefig('figs/水位与含沙量之间的散点图2.png', dpi=300, bbox_inches='tight')
plt.show()
plt.figure(figsize=(12,6))
sns.scatterplot(data=dfq1,x="水位", y="含沙量", hue="年",
palette="Set1",s = 60)
plt.xlabel("水位(m)")
plt.ylabel("含沙量(kg/"+"$m^3$"+")")
plt.title("")
plt.savefig('figs/水位与含沙量之间的散点图3.png', dpi=300, bbox_inches='tight')
plt.show()


含沙量和流量之间可能并不是简单的线性关系,还受到其他特征的影响。而且和前面与水位之间的数据分布很相似(可能使用其中的一个就能很好的表达含沙量)
目标1:解决方案,建立回归模型,分析他们之间的关系,预测含沙量
from sklearn.ensemble import RandomForestRegressor,GradientBoostingRegressor
from sklearn.svm import SVR,LinearSVR
from sklearn.tree import *
from sklearn.metrics import *
from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import graphviz
import pydotplus
from IPython.display import Image
from io import StringIO
模型1:决策树回归模型
建立决策树回归模型对数据进行预测,使用默认参数

从模型对因变量的预测效果可以知道,模型很好的预测了数据的变化趋势
分析不同深度下在训练集和测试机上的预测精度

除了模型1:决策树回归模型外,后续还有模型2:随机森林回归、模型3: GBDT回归、模型4:支持向量机回归、模型5:全连接神经网络。文章来源:https://www.toymoban.com/news/detail-700500.html
完整代码+结果+思路文档下载:2023数学建模国赛E题完整代码和文档文章来源地址https://www.toymoban.com/news/detail-700500.html
到了这里,关于2023数学建模国赛E题黄河水沙监测数据分析完整代码分析+处理结果+思路文档的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!