LeetCode-77-组合-Toy模板网

这篇具有很好参考价值的文章主要介绍了LeetCode-77-组合。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

LeetCode-77-组合,算法,leetcode,算法

一：题目描述：

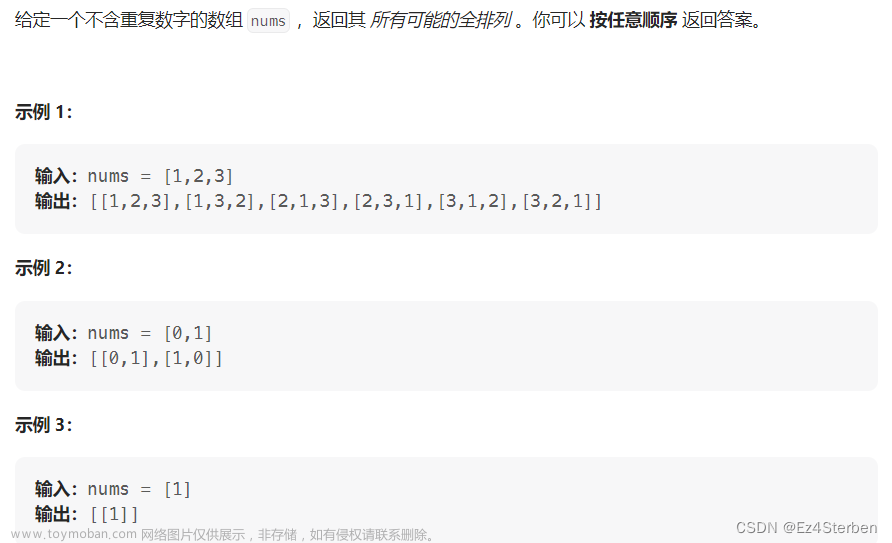
给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

二：示例与提示

示例 1:

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

示例 2:

输入：n = 1, k = 1
输出：[[1]]

提示：

1 <= n <= 20
1 <= k <= n

三：思路

回溯+剪枝

对于这类组合问题，可以将题目所描述的数组通过组合去构建一个树形结构

LeetCode-77-组合,算法,leetcode,算法

横向拓展是数组中的元素个数，从1到n
纵向拓展是深度，是对应元素的组合
通过不断的递归和回溯，在每一层次中构建组合，搜索到对应的叶子节点
图中每次搜索到了叶子节点，我们就找到了一个结果，将结果收集到结果集中即可

四：代码 + 复杂度分析

回溯+剪枝

/**
 * @param {number} n
 * @param {number} k
 * @return {number[][]}
 */
var combine = function(n, k) {
    //回溯
    //确定回溯函数的参数
    //存放最终所有结果的数组
    const res = []
    //path单层结果
    const path = []
    const backtracking = (n, k, index) => {
        //终止条件
        if(path.length === k) {
            console.log(path)
            //收集结果
            res.push([...path])
            return 
        }
        //单层逻辑
        for(let i = index; i <= n - (k - path.length) + 1; i++) {
            //路径收集
            path.push(i)
            //递归
            backtracking(n, k, i + 1)
            // console.log(path)
            //回溯
            path.pop()
        }
    }
    backtracking(n, k, 1)
    return res
};

时间复杂度：O(C（n， k）)
- 对于每个数字，我们有两个选择（包括或不包括），并且我们有k个选择（需要选择k个数字）
- 其中C(n, k)表示从n个元素中选择k个元素的组合数，也可以表示为二项式系数
空间复杂度：O(k + 2^n)文章来源地址https://www.toymoban.com/news/detail-701668.html
- 总的空间复杂度是 O(k + 2^n)，其中 k 反映了递归树的深度，而 2^n 反映了结果数组 res 的可能长度