十大经典排序算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了十大经典排序算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

十大经典排序算法

1、冒泡排序（Bubble Sort）：相邻元素比较，逐步将最大元素“冒泡”到序列最后。时间复杂度O(n^2)。

2、选择排序（Selection Sort）：从序列中选择最小的元素，放到序列的起始位置，再从剩余元素中选择最小的元素放到已排序序列的末尾。时间复杂度O(n^2)。

3、插入排序（Insertion Sort）：将序列分为已排序和未排序两部分，从未排序的部分选择元素插入到已排序的部分中，直到所有元素都被插入到已排序的部分。时间复杂度O(n^2)。

4、希尔排序（Shell Sort）：插入排序的改进版，通过设置增量序列分组进行排序，每组用插入排序。时间复杂度与增量序列的选取有关，平均时间复杂度为O(n^1.3)。

5、归并排序（Merge Sort）：将序列分成两个子序列，对每个子序列进行递归排序，然后合并两个有序子序列，直到合并成整个序列。时间复杂度O(nlogn)。

6、快速排序（Quick Sort）：选择枢轴将序列分成两部分，将小于枢轴的元素放在左边，大于枢轴的元素放在右边，然后递归地对左右两部分进行快速排序。时间复杂度O(nlogn)。

7、堆排序（Heap Sort）：使用堆的数据结构来维护序列，每次从堆顶选择最大（或最小）的元素，然后重新调整堆。时间复杂度O(nlogn)。

8、计数排序（Counting Sort）：统计每个元素出现的次数，然后根据元素出现的顺序将它们排好。时间复杂度O(n+k)，k是元素范围。

9、桶排序（Bucket Sort）：将元素分配到桶中，对每个桶中的元素进行排序，然后按照桶的顺序依次输出所有元素。时间复杂度O(n+k)。

10、基数排序（Radix Sort）：按照每个元素的位数进行排序，从低位到高位依次进行排序。时间复杂度O(dn)，d是最大数字的位数。

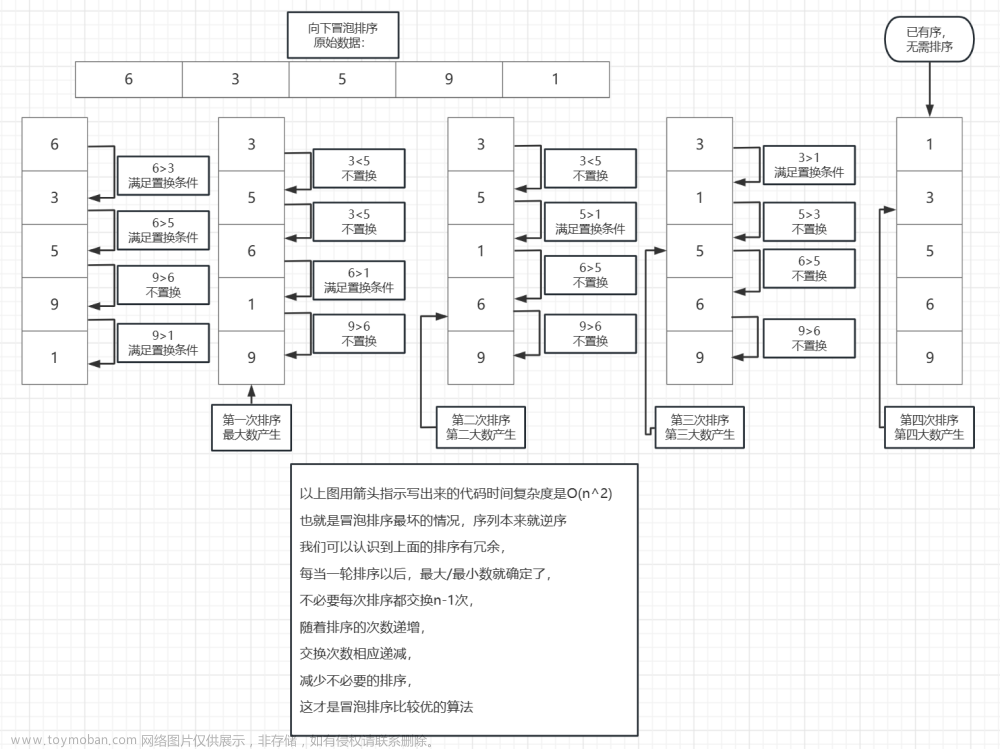
冒泡排序

冒泡排序是一种简单的排序算法，它通过不断地交换相邻的元素来将序列排序。具体步骤如下：

1、从序列的第一个元素开始，依次比较相邻的两个元素，如果前一个元素大于后一个元素，就交换它们的位置。

2、继续向后遍历序列，重复步骤1，直到遍历到最后一个元素。

3、重复执行步骤1和2，直到序列中的所有元素都排好序。

public static void bubbleSort(int[] arr) {
    int n = arr.length;
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                // 交换相邻的两个元素
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

这段代码使用了两层循环来实现冒泡排序。外层循环控制排序的趟数，内层循环控制每一趟的比较和交换。时间复杂度为O(n^2)，空间复杂度为O(1)。

选择排序

通过不断选择未排序部分的最小元素，将它们逐渐移到数组的开头。具体实现中，每一轮都从未排序部分的第一个元素开始，扫描整个未排序部分，找到其中的最小元素，然后将它和未排序部分的第一个元素交换位置。重复这个过程直到整个数组有序。

public static void selectionSort(int[] arr) {
    int n = arr.length;
    for (int i = 0; i < n - 1; i++) {
        int minIndex = i;
        for (int j = i + 1; j < n; j++) {
            if (arr[j] < arr[minIndex]) {
                minIndex = j;
            }
        }
        int temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
}

在该实现中，变量minIndex表示未排序部分的最小元素的下标。每次从未排序部分的第一个元素开始，扫描整个未排序部分，找到其中的最小元素，然后将它和未排序部分的第一个元素交换位置，以此将最小元素移到已排序部分的末尾。重复这个过程直到整个数组有序。

插入排序

通过不断将未排序部分中的元素插入到已排序部分中的适当位置，最终完成排序。

public static void insertionSort(int[] arr) {
    int len = arr.length;
    for (int i = 1; i < len; i++) {
        int j = i;
        int temp = arr[j];
        while (j > 0 && arr[j - 1] > temp) {
            //如果前一个元素比当前元素大，则将前一个元素向后移动一位。
            //将 j 的值减1，继续比较前一个元素。
            arr[j] = arr[j - 1];
            j--;
        }
        arr[j] = temp;
    }
}

希尔排序

希尔排序是插入排序的一种改进版本，也称为“缩小增量排序”。其思想是将原序列分成若干子序列，对每个子序列进行插入排序，然后缩小增量，继续进行排序，直到增量为1时完成排序。希尔排序的关键在于选择合适的增量序列。

选择一个增量序列，通常选择初始增量为数组长度的一半，每次将增量缩小一半，直到增量为1。
对于每个增量，将数组分成若干个子序列，分别对每个子序列进行插入排序。
对于较大的增量，子序列中相距较远的元素可以快速排序，减小增量后子序列中相距较近的元素已经接近有序，插入排序的效率高。
最后增量为1时，整个序列已经基本有序，插入排序的效率最高。

public static void shellSort(int[] arr) {
    int len = arr.length;
    int gap = len / 2; // 初始增量
    while (gap > 0) {
        // 对每个子序列进行插入排序
        for (int i = gap; i < len; i++) {
            int j = i;
            int temp = arr[j];
            while (j >= gap && arr[j - gap] > temp) {
                arr[j] = arr[j - gap];
                j -= gap;
            }
            arr[j] = temp;
        }
        gap /= 2; // 缩小增量
    }
}

在该实现中，变量gap表示增量，每次循环将gap除以2以缩小增量，直到gap为1时完成排序。在每次循环中，对于每个子序列（序列下标为i，步长为gap），使用插入排序的方法将子序列排序。

归并排序

归并排序是一种基于分治思想的排序算法。它的基本思想是将待排序数组分成若干个子数组，对每个子数组进行排序，然后将排好序的子数组合并成一个有序的数组。

具体步骤如下：

将待排序数组从中间分成两个子数组，递归地对左右两个子数组进行归并排序。
当子数组长度为1时，递归结束，返回结果。
合并左右两个排好序的子数组，得到新的有序数组。

下面是归并排序的Java代码实现：

public class MergeSort {
    public static void mergeSort(int[] arr, int left, int right) {
        if (left < right) {
            int mid = (left + right) / 2; // 将数组分成左右两部分
            mergeSort(arr, left, mid); // 对左半部分进行归并排序
            mergeSort(arr, mid + 1, right); // 对右半部分进行归并排序
            merge(arr, left, mid, right); // 将排好序的左右两部分合并
        }
    }

    private static void merge(int[] arr, int left, int mid, int right) {
        int[] temp = new int[right - left + 1]; // 创建临时数组
        int i = left; // 左半部分的指针
        int j = mid + 1; // 右半部分的指针
        int k = 0; // 临时数组的指针
        while (i <= mid && j <= right) {
            if (arr[i] < arr[j]) {
                temp[k++] = arr[i++];
            } else {
                temp[k++] = arr[j++];
            }
        }
        while (i <= mid) {
            temp[k++] = arr[i++];
        }
        while (j <= right) {
            temp[k++] = arr[j++];
        }
        // 将临时数组中的元素复制回原数组
        for (k = 0; k < temp.length; k++) {
            arr[left + k] = temp[k];
        }
    }

    public static void main(String[] args) {
        int[] arr = { 5, 3, 8, 6, 2, 7, 1, 4 };
        mergeSort(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(arr));
    }
}

在代码中，mergeSort方法是递归调用的归并排序方法，merge方法用于将排好序的左右两部分数组合并。归并排序的时间复杂度为O(nlogn)，空间复杂度为O(n)。

快速排序

快速排序是一种高效的排序算法，它基于分治的思想，通过不断地将序列分成更小的子序列，然后对子序列进行排序来达到整体排序的目的。具体步骤如下：

从序列中选择一个元素作为基准，称为枢轴（pivot）。
将序列中所有小于枢轴的元素移到枢轴左边，所有大于枢轴的元素移到枢轴右边，相同的元素可以放在任意一边。
对枢轴左右两边的子序列分别重复步骤1和步骤2，直到子序列的长度为1或0。

public static void quickSort(int[] arr, int left, int right) {
    if (left < right) {
        // 将数组分区，并返回分区点的位置
        int p = partition(arr, left, right);
        // 对分区点左右两边的子数组进行快速排序
        quickSort(arr, left, p - 1);
        quickSort(arr, p + 1, right);
    }
}

public static int partition(int[] arr, int left, int right) {
    int pivot = arr[left];  // 选择第一个元素为枢轴
    int i = left, j = right;
    while (i < j) {
        // 从右往左找到第一个小于枢轴的元素
        while (i < j && arr[j] >= pivot) {
            j--;
        }
        // 从左往右找到第一个大于枢轴的元素
        while (i < j && arr[i] <= pivot) {
            i++;
        }
        // 交换这两个元素
        if (i < j) {
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }
    // 将枢轴放到最终位置
    arr[left] = arr[i];
    arr[i] = pivot;
    return i;
}

这段代码使用了递归来实现快速排序。在每一次排序中，我们选择第一个元素作为枢轴，将序列分为两部分，并返回枢轴的位置。然后，对枢轴的左右两部分分别进行递归排序。时间复杂度为O(nlogn)，最坏情况下为O(n^2)，空间复杂度为O(logn)。

堆排序

堆排序是一种基于二叉堆的排序算法。它的基本思想是先将待排序数组构建成一个二叉堆，然后将堆顶元素取出，再将剩余元素重新构建成一个新的堆，如此反复，直到取出所有元素。

具体步骤如下：

将待排序数组构建成一个二叉堆，即从最后一个非叶子节点开始，依次执行下沉操作，直到根节点。
取出堆顶元素，将堆的最后一个元素放到堆顶，再从堆顶开始执行下沉操作，使得堆重新满足堆的性质。
重复步骤2，直到堆为空，即所有元素都已取出。

import java.util.Arrays;

public class HeapSort {
    // 堆排序方法
    public static void heapSort(int[] arr) {
        // 构建堆，从最后一个非叶子节点开始，依次执行下沉操作，直到根节点
        for (int i = arr.length / 2 - 1; i >= 0; i--) {
            percolateDown(arr, i, arr.length);
        }
        // 取出堆顶元素，将其放到有序区间的末尾，重构堆
        for (int i = arr.length - 1; i > 0; i--) {
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;
            // 重新构建堆
            percolateDown(arr, 0, i);
        }
    }

    // 下沉操作，用于维护堆的性质
    private static void percolateDown(int[] arr, int i, int n) {
        int parent = i;
        int child = 2 * i + 1;
        while (child < n) {
            // 找出左右子节点中较大的那个
            if (child + 1 < n && arr[child] < arr[child + 1]) {
                child++;
            }
            // 如果子节点比父节点大，就交换它们的位置
            if (arr[parent] < arr[child]) {
                int temp = arr[parent];
                arr[parent] = arr[child];
                arr[child] = temp;
                parent = child;
                child = 2 * parent + 1;
            } else {
                // 如果父节点比子节点大，说明已经满足堆的性质，跳出循环
                break;
            }
        }
    }

    public static void main(String[] args) {
        int[] arr = { 5, 3, 8, 6, 2, 7, 1, 4 };
        heapSort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

在代码中，heapSort方法用于执行堆排序，percolateDown方法用于下沉操作，即用于维护堆的性质。

计数排序

计数排序是一种非比较排序算法，它的基本思想是统计每个元素在序列中出现的次数，然后依次输出。

public static void countingSort(int[] arr) {
    if (arr == null || arr.length <= 1) {
        return;
    }

    int max = arr[0];
    int min = arr[0];
    int n = arr.length;

    // 找出待排序数组中的最大值和最小值
    for (int i = 1; i < n; i++) {
        if (arr[i] > max) {
            max = arr[i];
        } else if (arr[i] < min) {
            min = arr[i];
        }
    }

    int range = max - min + 1;

    // 计数数组，存储每个元素出现的次数
    int[] count = new int[range];

    // 统计待排序数组中每个元素出现的次数
    for (int i = 0; i < n; i++) {
        count[arr[i] - min]++;
    }

    // 累加计数数组中的元素
    for (int i = 1; i < range; i++) {
        count[i] += count[i - 1];
    }

    // 临时数组，存储排序后的结果
    int[] tmp = new int[n];

    // 从后往前遍历待排序数组，按照计数数组中的位置将元素放入临时数组中
    for (int i = n - 1; i >= 0; i--) {
        int index = count[arr[i] - min] - 1;
        tmp[index] = arr[i];
        count[arr[i] - min]--;
    }

    // 将临时数组中的元素拷贝回原数组
    System.arraycopy(tmp, 0, arr, 0, n);
}

桶排序

桶排序（Bucket Sort）是一种线性排序算法，它利用了函数的映射关系，将要排序的数据分到有限数量的桶中，再对每个桶里的数据进行单独排序。

实现桶排序的一般步骤如下：

确定待排序数组中最大值和最小值；
创建若干个桶，根据待排序数据的范围将数据放入相应的桶中；
对每个非空的桶中的数据进行排序，可以使用插入排序等算法；
将所有桶中的数据按顺序合并起来即可。

public static void bucketSort(int[] arr) {
    int n = arr.length;
    int maxVal = arr[0];
    int minVal = arr[0];
    for (int i = 1; i < n; i++) {
        maxVal = Math.max(maxVal, arr[i]);
        minVal = Math.min(minVal, arr[i]);
    }

    // 计算桶的个数，并创建桶
    int bucketCount = (maxVal - minVal) / n + 1;
    List<List<Integer>> buckets = new ArrayList<>(bucketCount);
    for (int i = 0; i < bucketCount; i++) {
        buckets.add(new ArrayList<>());
    }

    // 将数据分到各个桶中
    for (int i = 0; i < n; i++) {
        int bucketIdx = (arr[i] - minVal) / n;
        buckets.get(bucketIdx).add(arr[i]);
    }

    // 对每个桶中的数据进行排序
    for (int i = 0; i < bucketCount; i++) {
        Collections.sort(buckets.get(i));
    }

    // 将所有桶中的数据按顺序合并起来
    int idx = 0;
    for (int i = 0; i < bucketCount; i++) {
        List<Integer> bucket = buckets.get(i);
        for (int j = 0; j < bucket.size(); j++) {
            arr[idx++] = bucket.get(j);
        }
    }
}

在这个实现中，我们首先找出待排序数组中的最大值和最小值，然后根据数据的范围确定桶的数量。接着，我们将待排序数据放入对应的桶中，对每个桶中的数据进行排序，最后将所有桶中的数据按顺序合并起来，得到排序后的数组。

基数排序

基数排序（Radix Sort）是一种非比较排序算法，它将整数按位数切割成不同的数字，然后按每个位数分别比较。基数排序属于稳定排序，时间复杂度为O(d(n+r))，其中n是排序元素个数，d是数字位数，r是基数。它的主要思想是：将待排序的整数拆分成多个数字位上的值，然后从最低位到最高位依次对每个数字位上的值进行排序。

public static void radixSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    
    // 找出数组中的最大值，以便确定数字的位数
    int maxVal = arr[0];
    for (int i = 1; i < arr.length; i++) {
        maxVal = Math.max(maxVal, arr[i]);
    }
    
    // 根据数字的位数依次进行排序
    for (int exp = 1; maxVal / exp > 0; exp *= 10) {
        // 初始化桶，用于存储每个数字位上的值
        int[] bucket = new int[10];
        // 统计每个桶中的元素个数
        for (int i = 0; i < arr.length; i++) {
            int digit = (arr[i] / exp) % 10;
            bucket[digit]++;
        }
        // 统计桶中的前缀和
        for (int i = 1; i < bucket.length; i++) {
            bucket[i] += bucket[i - 1];
        }
        // 将数组中的元素按照当前数字位上的值依次存放到新数组中
        int[] sortedArr = new int[arr.length];
        for (int i = arr.length - 1; i >= 0; i--) {
            int digit = (arr[i] / exp) % 10;
            sortedArr[--bucket[digit]] = arr[i];
        }
        // 将排序后的数组复制回原数组
        System.arraycopy(sortedArr, 0, arr, 0, arr.length);
    }
}

在上面的代码中，我们首先找出了待排序数组中的最大值，以便确定数字的位数，然后依次对每个数字位上的值进行排序。具体来说，我们利用了桶排序的思想，在每次排序时都需要初始化桶，并统计每个桶中的元素个数。接着，我们根据桶中元素的前缀和，计算出每个数字位上的值在排序后的数组中的结束位置，从而将待排序数组中的元素依次存放到新数组中。最后，将排序后的数组复制回原数组，即可得到排好序的结果。文章来源地址https://www.toymoban.com/news/detail-702235.html

到了这里，关于十大经典排序算法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！