算法设计与分析学习笔记之二分查找算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了算法设计与分析学习笔记之二分查找算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

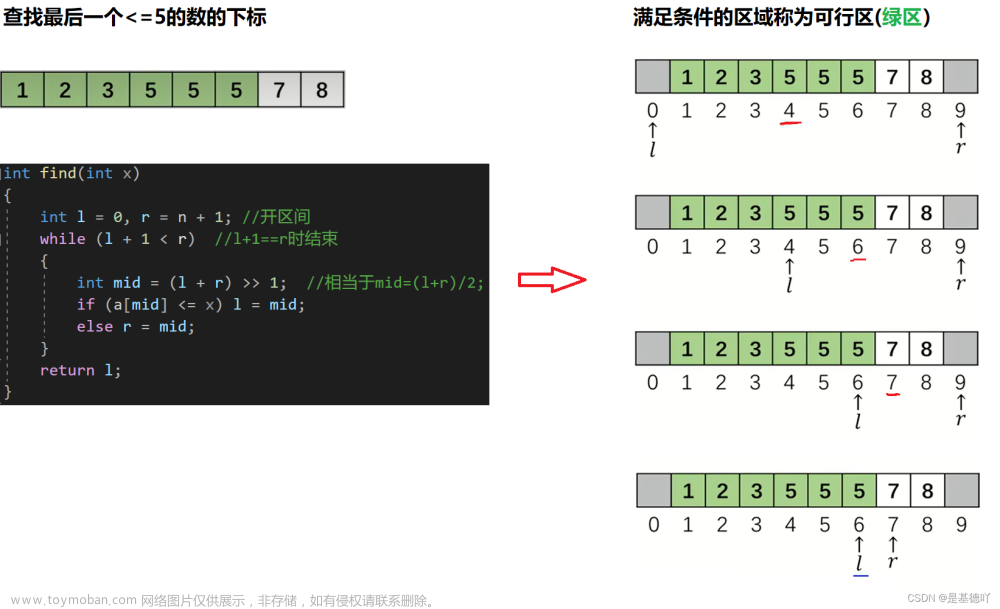
二分查找只适用于有序的顺序表，非严格递增或是非严格递减都行。

二分查找运用到了分治的思想，将整体逐渐分为许多个小的部分，让整体的解变为诸多小部分解的合成，要求整体可以分解，小部分的解汇合之后可以得到整体部分的解。

循环写法：

int binarySearch(int[] array, int n, int searchNum) {
        int low = 0;
        int high = n - 1;
        while (low <= high) {
            // 找出中间下标 
            int mid = low + ((high - low) >> 1);
            // 每次都设置所求区间的中间位置，和中间位置的数字作比较
            // (high - low) >> 1中的>>是右移运算符，等于'/2'
            if (nums[mid] > search_num) {
                high = mid - 1;
            } else if (nums[mid] < search_num) {
                low = mid + 1;
            } else {
                return mid;
            }
        }
        return -1;
        }

递归写法：

int recursiveBserach(int[] nums, int low, int high, int value) {
        if (low > high) return -1;
        // 每次都设置所求区间的中间位置，和中间位置的数字作比较
        int mid = low + ((high - low) >> 1);
 		// (high - low) >> 1中的>>是右移运算符，等于'/2'
		if (nums[mid] > search_num) {
            return recursiveBserach(nums, low, mid - 1, value);
        } else if (nums[mid] < search_num) {
            return recursiveBserach(nums, mid + 1, high, value);
        } else {
            return mid;
        }
    }