简单介绍一下我自己:博主专注建模四年,参与过大大小小数十来次数学建模,理解各类模型原理以及每种模型的建模流程和各类题目分析方法。参与过十余次数学建模大赛,三次美赛获得过二次M奖一次H奖,国赛二等奖。希望各位以后遇到建模比赛可以艾特一下我,我可以提供免费的思路和部分源码,以后的数模比赛只要我还有时间肯定会第一时间写出免费开源思路。博主紧跟各类数模比赛,每场数模竞赛博主都会将最新的思路和代码写进此专栏以及详细思路和完全代码且完全免费。希望有需求的小伙伴不要错过笔者精心打造的文章。
一文速学-数学建模常用模型https://blog.csdn.net/master_hunter/category_10967944.html
前两问都已经解决且都有对应的详解思路和源代码,直接运行就可以出来结果了:
2023全国大学生数学建模竞赛E题详解+Python代码源码(二)https://zhuanlan.zhihu.com/p/6549772172023全国大学生数学建模竞赛-E 题思路详解+Python代码源码解析https://zhuanlan.zhihu.com/p/654941615只希望!大家给我三连就满足了!那么废话不多说现在开始做题。
第三问
问题 3 根据该水文站水沙通量的变化规律,预测分析该水文站未来两年水沙通量的变化 趋势,并为该水文站制订未来两年最优的采样监测方案(采样监测次数和具体时间等),使其 既能及时掌握水沙通量的动态变化情况,又能最大程度地减少监测成本资源。
题解
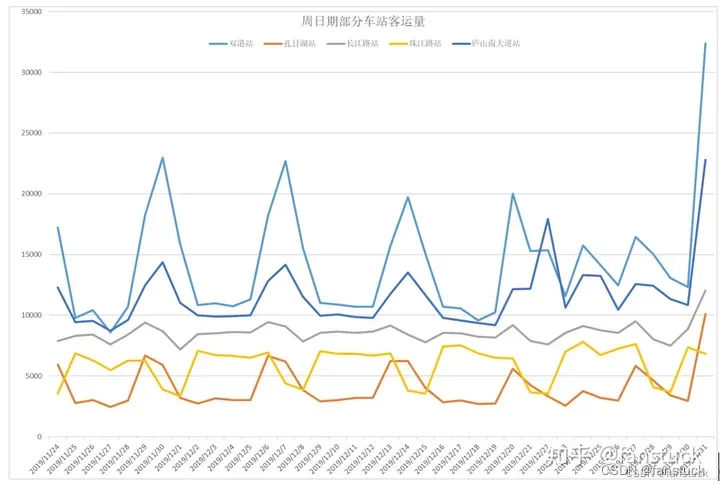
根据之前我们的第一问和第二问,可以确定水文站水沙通量数据就是十分典型的季节时间序列数据,描述这类序列的模型称作季节时间序列模型(seasonal ARIMA model),用SARIMA表示。季节时间序列模型也称作乘积季节模型(Multiplicative seasonal model)。因为模型的最终形式是用因子相乘的形式表示。例如周日期部分车站客运量:

关于时间序列分析预测算法我基本已经全部写了:


想要详细了解的可以去看看笔者的专栏:
一文速学-数学建模常用模型https://blog.csdn.net/master_hunter/category_10967944.html
给大家普及一下平稳时间序列和白噪声序列。平稳是指宽平稳,其特性是序列的统计特性不随时间的平移而变化,即均值和协方差不随时间的平移而变化。 时间序列是指将某种现象某一个统计指标在不同时间上的各个数值,按时间先后顺序排列而形成的序列。平稳时间序列粗略地讲,一个时间序列,如果均值没有系统的变化(无趋势)、方差没有系统变化,且严格消除了周期性变化,就称之是平稳的。
平稳时间序列是时间序列分析中最重要的特殊类型。到目前为止,时间序列分析基本上是以平稳时间序列为基础的,对于非平稳时间序列的统计分析,其方法和理论都很有局限性。若一个平稳时间序列的序列值之间没有相关性,那么就意味着这种数据前后没有规律,也就无法挖掘出有效的信息,这种序列称为纯随机序列。在纯随机序列中,有一种序列称为白噪声序列,这种序列随机且各期的方差一致。平稳时间序列分析在于充分挖掘时间序列之间的关系,当时间序列中的关系被提取出来后,剩下的序列就应该是个白噪声序列。
水文站水沙通量数据呈现一定的周期性波动,描述这类序列的模型称作季节时间序列模型(seasonal ARIMA model),用SARIMA表示。季节时间序列模型也称作乘积季节模型(Multiplicative seasonal model)。因为模型的最终形式是用因子相乘的形式表示。
SARIMA模型定义
SARIMA(Seasonal Autoregressive Integrated Moving Average)是一种基于 ARIMA 模型的季节时间序列预测模型。ARIMA 模型是一种广泛应用于时间序列预测的经典模型,它考虑了时间序列的趋势性和周期性。SARIMA 模型在 ARIMA 模型的基础上增加了季节性,因此可以更好地应对具有季节性变化的时间序列数据。
SARIMA 模型通常包含以下几个参数:
- 季节周期 (Seasonal period):时间序列数据呈现季节性变化的周期,例如一年、一周、一天等。
- 差分次数 (Order of differencing):对时间序列数据进行差分的次数,以消除数据的非平稳性。
- 自回归项 (Autoregressive terms):用于建立时间序列与其过去值的关系,表示时间序列数据的趋势性。
- 移动平均项 (Moving average terms):用于建立时间序列的随机波动性与过去的误差的关系,表示时间序列数据的随机性。
SARIMA 模型可以用来预测具有季节性变化的时间序列数据,例如销售额、气温、股票价格等。它需要基于历史数据来拟合模型,然后使用模型来预测未来一段时间内的数据。在使用 SARIMA 模型时,需要选择合适的参数和模型结构,并进行模型诊断和调优,以获得更准确的预测结果。
这里就不展示具体的建模过程了,想要具体的建模过程可以去看笔者的专栏文章:
一文速学数模-季节性时序预测SARIMA模型详解+Python实现https://blog.csdn.net/master_hunter/article/details/130236047
给出流程图我们直接开始建模:
1.数据预处理
根据建模步骤我们首先对时间序列数据进行平稳性校验和季节性差分等操作。如果数据不平稳,需要进行差分操作使其变为平稳时间序列。同时,如果数据具有季节性,需要对其进行季节性差分,消除季节性影响。
观察时序图
将水位和流量的时序图绘制出来,观察是否存在明显的趋势、季节性和周期性。
我们可以看到数据有上升的趋势,可以定性地判断该序列非平稳。可以使用seasonal_decompose()进行分析,将时间序列分解成长期趋势项(Trend)、季节性周期项(Seansonal)和残差项(Resid)这三部分。
差分(Differencing)
如果数据存在趋势或季节性,可以进行差分,直到数据变得稳定。
ADF检验
ARIMA模型要求时间序列是平稳的。所谓平稳性,其基本思想是:决定过程特性的统计规律不随着时间的变化而变化。

通过观察ACF和PACF图,可以看到哪些滞后值是显著的,从而得到p和q的估计。如果想要深度了解获取源码我的专栏文章有:

文章来源:https://www.toymoban.com/news/detail-704049.html
stableCheck(df_with_sediment['水位(m)'])
- 测试统计量(Test Statistic):它是检验的关键指标之一。如果它小于某个临界值,我们可以拒绝原假设。更负数的统计量表明序列更有可能是平稳的
- p-value:它表示在原假设成立的情况下,观察到测试统计量或更极端结果的概率。通常情况下,如果p-value低于显著性水平(如0.05),我们就会拒绝原假设。
- 滞后阶数(Lags Used):这是在回归中使用的滞后阶数,用于建立AR模型。
- 观察数量(Number of Observations Used):这表示在分析中使用的样本数量。
-
临界值(Critical Value):在给定的显著性水平下,这是测试统计量的阈值。如果测试统计量小于这个阈值,我们可以拒绝原假设。
- 1%显著性水平的临界值
- 5%显著性水平的临界值
- 10%显著性水平的临界值
在上述ADF检验的结果中:
- 测试统计量为-5.253766,它小于所有显著性水平下的临界值,表明我们可以拒绝原假设。
- p-value为0.000007,非常接近于零,这也支持了拒绝原假设的结论。
可以得出结论:在给定的显著性水平下,时间序列是稳定的,拒绝了存在单位根(非平稳)的原假设。
那么现在需要确定p,d,q的值。

最后建立SARIMA模型即可:

print(f'Mean Squared Error (Water Level): {mse_water}')
Mean Squared Error (Water Level): 0.06271951521945275(下一次更新源码版本)马上开做第四问。文章来源地址https://www.toymoban.com/news/detail-704049.html
到了这里,关于2023全国大学生数学建模竞赛E题详解+Python代码源码(三)SARIMA模型的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!