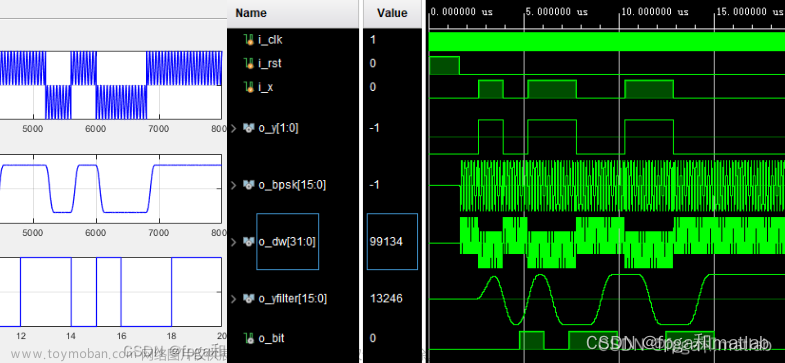
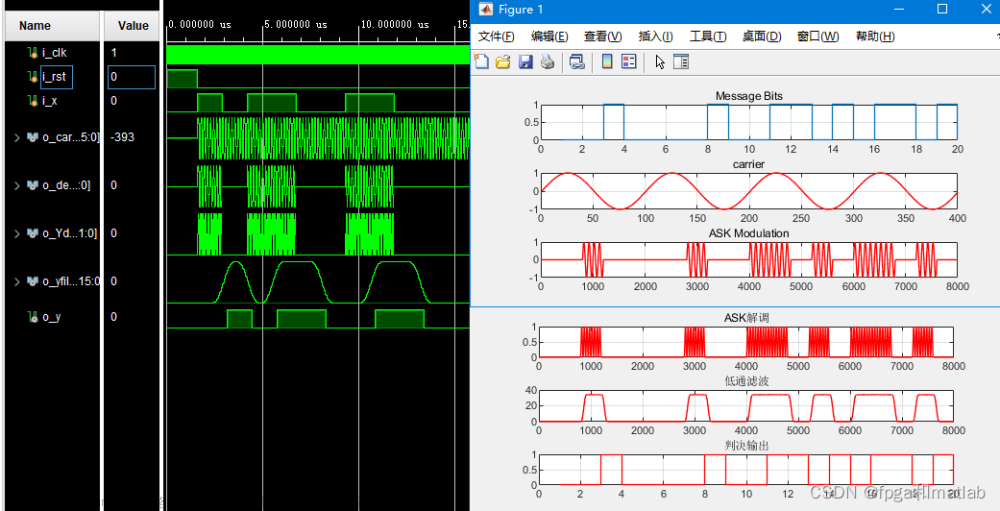
常规单脉冲和差比幅测角原理
设方位（或俯仰）平面内单个波束的方向图函数为
F
(
θ
)
F(\theta)
F(θ)，两波束各自相对天线轴线的波束偏角为
δ
\delta
δ，设目标偏离天线轴线的角度为
θ
\theta
θ，则有
F
∑
(
θ
)
=
F
(
δ
−
θ
)
+
F
(
δ
+
θ
)
=
F
(
θ
−
δ
)
+
F
(
θ
+
δ
)
F
Δ
(
θ
)
=
F
(
δ
−
θ
)
−
F
(
δ
+
θ
)
=
F
(
θ
−
δ
)
−
F
(
θ
+
δ
)
F_{\sum}(\theta)=F(\delta-\theta)+F(\delta+\theta)=F(\theta-\delta)+F(\theta+\delta)\\F_{\Delta}(\theta)=F(\delta-\theta)-F(\delta+\theta)=F(\theta-\delta)-F(\theta+\delta)
F∑(θ)=F(δ−θ)+F(δ+θ)=F(θ−δ)+F(θ+δ)FΔ(θ)=F(δ−θ)−F(δ+θ)=F(θ−δ)−F(θ+δ)
F
∑
(
θ
)
F_{\sum}(\theta)
F∑(θ)表示和通道和方向图，
F
Δ
(
θ
)
F_{\Delta}(\theta)
FΔ(θ)表示差通道差方向图，和差通道方向图函数如图所示。
对于单脉冲信号，和通道接收信号
E
∑
E_{\sum}
E∑以及差通道接收信号
E
Δ
E_{\Delta}
EΔ可以分别表示为
E
∑
=
A
∑
(
θ
)
e
x
p
(
−
j
2
k
R
)
E
Δ
=
A
Δ
(
θ
)
e
x
p
(
−
j
2
k
R
)
E_{\sum}=A_{\sum}(\theta)exp(-j2kR)\\E_{\Delta}=A_{\Delta}(\theta)exp(-j2kR)
E∑=A∑(θ)exp(−j2kR)EΔ=AΔ(θ)exp(−j2kR)
式中，
k
=
2
π
λ
k=\frac {2\pi}{\lambda}
k=λ2π是波数，R是目标和观测点之间的相对视线距离。
将差方向图函数展开成麦克劳林级数，用差通道信号比上和通道信号就可求得目标偏离天线轴线的角度，那么
θ
\theta
θ可表示为
θ
=
E
Δ
E
∑
=
A
Δ
(
θ
)
A
∑
(
θ
)
\theta=\frac {E_{\Delta}}{E_{\sum}}=\frac {A_{\Delta}(\theta)}{A_{\sum}(\theta)}
θ=E∑EΔ=A∑(θ)AΔ(θ)
和差幅度测角matlab
（1）方向图仿真结果
（2）测角结果
基于FFT的频域单脉冲比幅测角原理
设目标上有M个散射点，则目标整体的回波经过混频解调处理后可以表示为
E
(
t
)
=
∑
i
=
1
M
A
i
(
t
)
e
x
p
(
−
j
k
R
i
)
E(t)=\sum_{i=1}^{M}A_{i}(t)exp(-jkR_i)
E(t)=i=1∑MAi(t)exp(−jkRi)
式中，
k
=
2
π
λ
k=\frac {2\pi}{\lambda}
k=λ2π是波数,
A
i
(
t
)
A_{i}(t)
Ai(t)和
R
i
R_i
Ri分别表示第i个散射点的回波幅度和距离观测雷达的径向距离。在高重频体制下，可以近似认为在一帧的信号处理周期内弹目相对径向加速度不变，
R
i
R_i
Ri可以进一步表示为，
R
i
=
R
i
0
−
(
V
i
0
t
+
0.5
a
i
t
2
)
R_i=R_{i0}-(V_{i0}t+0.5a_it^2)
Ri=Ri0−(Vi0t+0.5ait2),
R
i
0
R_{i0}
Ri0,
V
i
0
V_{i0}
Vi0和
a
i
a_i
ai分别表示第i个散射点距离观测雷达的初始径向距离，初始相对径向速度和相对径向加速度，将其代入上式可得
E
(
t
)
=
∑
i
=
1
M
A
i
(
t
)
e
x
p
(
j
2
π
f
i
d
t
−
j
k
R
i
0
)
E(t)=\sum_{i=1}^{M}A_{i}(t)exp(j2\pi f_{id} t-jkR_{i0})
E(t)=i=1∑MAi(t)exp(j2πfidt−jkRi0)
下面以单个散射点为例来推导基于频域仿形的单脉冲比幅测角过程。考虑第i个散射点的回波信号，经过采样得到的数字信号表示为
E
i
(
n
)
=
A
i
(
n
)
e
x
p
(
j
2
π
ω
i
d
n
−
j
2
k
R
i
0
)
E_{i}(n)=A_i(n)exp(j2\pi\omega_{id}n-j2kR_{i0})
Ei(n)=Ai(n)exp(j2πωidn−j2kRi0)
式中
ω
i
d
\omega_{id}
ωid表示数字多普勒频率，
ω
i
d
=
f
i
d
T
\omega_{id}=f_{id}T
ωid=fidT,
T
T
T是采样周期。回波信号进入和、差通道后分别得到输出信号
E
i
∑
(
n
)
=
A
i
∑
(
n
)
e
x
p
(
j
2
π
ω
i
d
n
−
j
2
k
R
i
0
)
E
i
Δ
(
n
)
=
A
i
Δ
(
n
)
e
x
p
(
j
2
π
ω
i
d
n
−
j
2
k
R
i
0
)
E_{i\sum}(n)=A_{i\sum}(n)exp(j2\pi\omega_{id}n-j2kR_{i0})\\E_{i\Delta}(n)=A_{i\Delta}(n)exp(j2\pi\omega_{id}n-j2kR_{i0})
Ei∑(n)=Ai∑(n)exp(j2πωidn−j2kRi0)EiΔ(n)=AiΔ(n)exp(j2πωidn−j2kRi0)
对和、差通道的输出信号分别做FFT处理，得到和、差通道的输出信号频谱表达式如下
X
i
∑
(
l
)
=
F
F
T
[
E
i
∑
]
X
i
Δ
(
l
)
=
F
F
T
[
E
i
Δ
]
X_{i\sum}(l)=FFT[E_{i\sum}]\\X_{i\Delta}(l)=FFT[E_{i\Delta}]
Xi∑(l)=FFT[Ei∑]XiΔ(l)=FFT[EiΔ]
以但散射点为例，用第i个散射点的差通道频谱分量比上和通道频谱分量，可以得到第i个散射点的角度测量公式如下
θ
i
=
X
i
Δ
(
l
i
)
X
i
∑
(
l
i
)
\theta_{i}=\frac {X_{i\Delta}(l_{i})}{X_{i\sum}(l_{i})}
θi=Xi∑(li)XiΔ(li)
基于FFT的和差幅度测角matlab
（1）16点滑窗FFT
（2）32点滑窗FFT
（3）64点滑窗FFT
文章来源：https://www.toymoban.com/news/detail-704434.html
（4）128点滑窗FFT
从测角结果可以看出，基于FFT的和差幅度测角相较于常规和差幅度测角精度有所提升，同时128点滑窗FFT测角误差最小文章来源地址https://www.toymoban.com/news/detail-704434.html
和差幅度测角FPGA / 解模糊
到了这里，关于双天线和差测角matlab / FPGA开发的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
