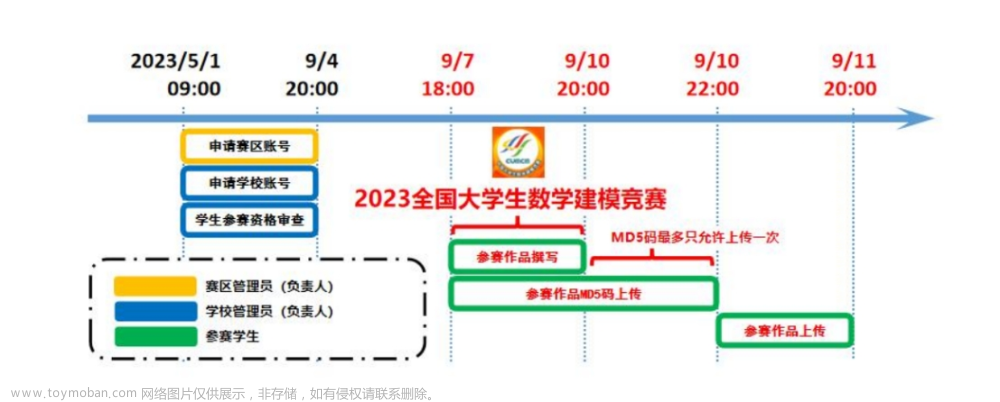
2023年全国大学生数学建模竞赛A题定日镜场的优化设计,目前已写出第四版国赛A题思路和模型详细公式,目录如下:
-
一、 问题重述... 1
-
二、 问题分析... 1
-
三、 模型假设... 6
-
四、 问题一模型的建立和求解... 6
-
4.1 定日镜场坐标系的建立... 6
-
4.2 定日镜相关参数及顶点坐标计算... 7
-
4.2.1 定日镜镜面法向量及俯仰角的计算... 7
-
4.2.2 定日镜顶点坐标的计算... 8
-
4.3 效率模型的建立... 10
-
4.3.1 余弦效率计算模型... 11
-
4.3.2 阴影遮挡效率模型... 13
-
4.3.3 集热器截断效率模型... 16
-
4.4 问题一模型的求解... 19
-
五、 问题二模型的建立和求解... 20
-
5.1 模型求解变量维度简化... 20
-
5.2 镜场的几何布局形式... 21
-
5.2.1 放射状栅格法... 21
-
5.2.2 密集型Campo规则布置法... 22
详细的模型和后续更新代码下载见文末地址 。后续持续更新

2023国赛A题题目:构建以新能源为主体的新型电力系统,是我国实现“碳达峰 ”“ 碳中和 ”目标的一 项重要措施。塔式太阳能光热发电是一种低碳环保的新型清洁能源技术 。
定日镜是塔式太阳能光热发电站(以下简称塔式电站)收集太阳能的基本组件,其 底座由纵向转轴和水平转轴组成,平面反射镜安装在水平转轴上。纵向转轴的轴线与地面垂直,可以控制反射镜的方位角。水平转轴的轴线与地面平行,可以控制反射镜的 俯仰 角,定日镜及底座示意图见图 1。两转轴的交点(也是定日镜中心) 离地面的高度 称为定日镜的安装高度。塔式电站利用大量的定日镜组成阵列,称为定日镜场 。定日镜 将太阳光反射汇聚到 安装在 镜场中吸收塔 顶端 上的 集热器,加热其中的导热介质,并将太阳能以热能形式储存起来 ,再经过热交换实现由热能向电能的转化。 太阳光并非平行光线, 而是具有一定锥形角的 一束 锥形光线 ,因此太阳入射光线 经定日镜 任意 一点的反射光线 也是一束 锥形光线 [2 ]。定日镜在工作时,控制系统根据太阳的位置实时控制定日镜的法 向,使得太阳中心 点发出的光线 经定日镜中心 反射后 指向 集热器中心 。集热器中心的离地高度称为吸收塔高度。

现计划在中心位于东经98.5∘,北纬39.4∘,海拔3000m,半径350m的圆形区域内建设一个圆形定日镜场(图2)。以圆形区域中心为原点,正东方向为 轴正向,正北方向为 轴正向,垂直于地面向上方向为z轴正向建立坐标系,称为镜场坐标系。
规划的吸收塔高度为80m,集热器采用高8m、直径7m的圆柱形外表受光式集热器。吸收塔周围100m范围内不安装定日镜,留出空地建造厂房,用于安装发电、储能、控制等设备。定日镜的形状为平面矩形,其上下两条边始终平行于地面,这两条边之间的距离称为镜面高度,镜面左右两条边之间的距离称为镜面宽度,通常镜面宽度不小于镜面高度(约束条件1)。镜面边长在2m至8m之间,安装高度在2m至6m之间(问题2问题3的模型自变量优化求解区间限制),安装高度必须保证镜面在绕水平转轴旋转时不会触及地面(约束条件2)。由于维护及清洗车辆行驶的需要,要求相邻定日镜底座中心之间的距离比镜面宽度多5m以上。(约束条件3)
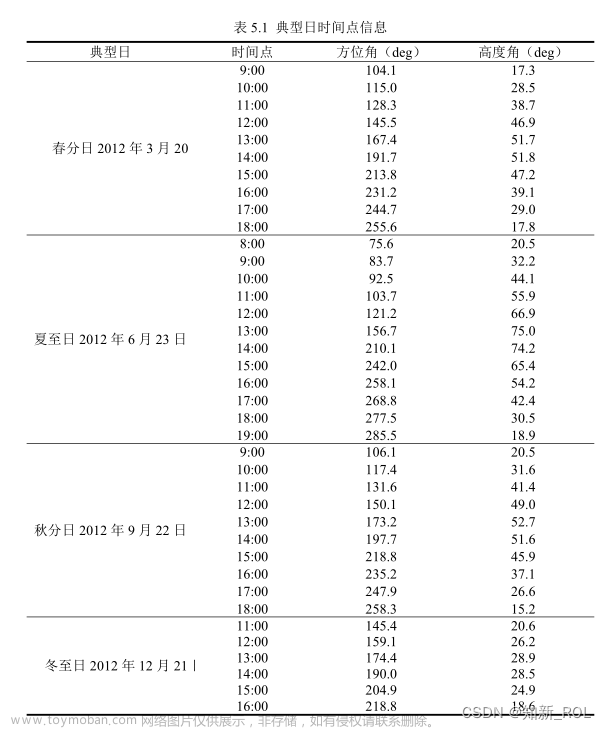
为简化计算,本问题中所有“年均”指标的计算时点均为当地时间每月21日9:00、10:30、12:00、13:30、15:00。(只需要计算12*5个时间点)

2023年全国大学生数学建模国赛A题题目:
请建立模型解决以下问题:
问题分析
国赛A题问题1:若将吸收塔建于该圆形定日镜场中心,定日镜尺寸均为6m×6m,安装高度均为4m,且给定所有定日镜中心的位置(坐标已知,可根据附录相关公式计算一些中间量)(以下简称为定日镜位置,相关数据见附件),请计算该定日镜场的年平均光学效率、年平均输出热功率,以及单位镜面面积年平均输出热功率(光学效率及输出热功率的定义见附录)。请将结果分别按表1和表2的格式填入表格。
关键点:(附录已经给出相关公式,建立一个在第1问给定条件下的计算该定日镜场的年平均光学效率、年平均输出热功率,以及单位镜面面积年平均输出热功率的数学模型,直接进行求解即可,这一问的准确性会影响后面几问,因此需要准确建模)
国赛A题问题2:按设计要求,定日镜场的额定年平均输出热功率(以下简称额定功率)为60MW。若所有定日镜尺寸及安装高度相同,请设计定日镜场的以下参数(需要建立根据第1问的模型,第1问的模型是一个内部模型,外部再套一个优化模型):吸收塔的位置坐标(2个变量)、定日镜尺寸(1个变量)、安装高度(1个变量)、定日镜数目(1个变量,N)、定日镜位置(2N个变量)(优化变量),使得定日镜场在达到额定功率的条件(约束条件4)下,单位镜面面积年平均输出热功率尽量大(优化目标函数)。请将结果分别按表1、2、3的格式填入表格,并将吸收塔的位置坐标、定日镜尺寸、安装高度、位置坐标按模板规定的格式保存到result2.xlsx文件中。
国赛A题问题3:如果定日镜尺寸可以不同,安装高度也可以不同,额定功率设置同问题2,请重新设计定日镜场的各个参数,使得定日镜场在达到额定功率的条件下,单位镜面面积年平均输出热功率尽量大。请将结果分别按表1、表2和表3的格式填入表格,并将吸收塔的位置坐标(2个变量)、各定日镜尺寸(N个变量)、安装高度(N个变量)、位置坐标(2N个变量)按模板规定的格式保存到result3.xlsx文件中。(这里同问题2,只是求解变量变多,问题复杂度进一步提高)
可以看到,问题2、问题3是基于问题1的几何模型进行优化,因此主要是问题1的几何模型的建立,后面优化问题可以使用各种优化算法求解,但是同时这里的优化变量很多,因此需要在优化问题的简化与算法的选择方面进行一定的考虑,这也是最后评奖的一个重点。
另外一个重点就是问题1的几何模型建立,这一问的建模准确性对结果的影响很大,评委可以直接根据结果答案的正确性区分奖项,因此需要冲奖的同学需要重视这一问。


附录相关计算公式

公式的理解:太阳高度角与3个变量有关,当地纬度、太阳时角、太阳赤纬角。其中纬度已知,太阳时角与时间有关(一天5个时间),太阳赤纬角与天数有关(一共12个月,每月21号,因此有12天)。所以对于每个时间(一共5*12个时间),太阳高度角都是确定的。

公式理解:海拔高度已知,太阳高度角前面已经计算出来,所以对于每个时间(一共5*12个时间),DNI是确定的。

公式理解:DNI已经算出来了,所以输出热功率只与面积和光学效率有关。采光面积应该是定值,即长乘宽


计算步骤如下:给定镜面中心的坐标位置,可以直接计算dHR,进而计算大气透射率,镜面反射率为定值,因此还剩下3个效率需要建模和计算(这是我们需要建立的主要的模型)
详细的模型和代码下载见文末地址。
模型假设
(1)定日镜场为圆形,定日镜场采用径向交错的布置方案,以中心塔为圆心进行周向均匀布置。为了便于突出太阳位置对阴影遮挡效率的影响,镜场中的定日镜以不发生机械碰撞为原则,建立密集型的仿真镜场。
(2)镜场平面为理想的水平面,且所有定日镜的立柱高度一致。所有定日镜规格一致且为矩形,定日镜均采用高度角-方位角跟踪方式,并假定定日镜镜面为理想平面。
问题一模型的建立和求解
定日镜场坐标系的建立
塔式光热电站的定日镜场多以集热塔为中心进行周向布置,不论是圆形的辐射式镜场还是方形的麦田型镜场均可用以集热塔为坐标原点的空间直角坐标系来表征镜场中各个定日镜的方位。为了便于同时描述太阳与定日镜的位置,本文将使用以吸热塔中轴线与定日镜场平面的交点为坐标原点的地平坐标系来当作定日镜场坐标系。即以吸热塔底座的几何中心为坐标系原点O,将正东方向指定为坐标系X正半轴,正北方向指定为坐标系Y正半轴,天顶方向指定为坐标系Z轴正半轴,建立的镜场三维空间直角坐标系如图所示。

旋转矩阵
在进行坐标转换的时候,需要确定镜面坐标系与地面坐标系的转换关系,即需要使用到旋转矩阵。
绕x\y\z轴旋转的旋转矩阵如下:绕x轴进行旋转(在yz平面顺时针旋转)


绕y轴进行旋转(在zx平面顺时针旋转)


绕z轴进行旋转(在xy平面顺时针旋转)


由题目可知,定日镜在工作时,控制系统根据太阳的位置实时控制定日镜的法向,使得太阳中心点发出的光线经定日镜中心反射后指向集热器中心。根据这一条件可以确定镜面的方向,也就是镜面坐标系与地面坐标系的转换关系,即旋转矩阵。
定日镜相关参数及顶点坐标计算
因为定日镜场的综合效率并不是各个单一定日镜效率的简单叠加或相乘,因此在定日镜的仿真研究中常常需要通过计算定日镜各个顶点在空间中的坐标来确定目标定日镜与相邻定日镜之间的相互关系。尤其在阴影遮挡效率的计算过程中还需要将目标定日镜向其他定日镜所在的平面进行投影来确定是否发生阴影或遮挡,因此建立定日镜场效率模型的第一步就是计算定日镜的相关参数及顶点坐标。文章来源:https://www.toymoban.com/news/detail-704461.html
完整详细的模型和代码下载见:2023数学建模国赛A题思路模型文章来源地址https://www.toymoban.com/news/detail-704461.html
到了这里,关于【2023数学建模国赛】A题定日镜场的优化设计模型建立的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!