选择对 EB布局进行更深入的研究,主要探究其布局关键参数方位间距因子 Asf和极限重置因子 Arlim如何取值可以得到光学性能更好的定日镜场。故选择应用改进后的混合策略鲸鱼优化算法对
EB布局进行优化,同时结合实例 Gemasolar电站相关数据进行验证分析。
5.1目标函数的构建
5.1.1优化目标与工程案例
在对基于辐射网格布局和无遮挡布局所衍生出的 EB、No blocking-dense和 DELSOL布局模式进行研究以及仿真后,发现按前两种模式布局后的镜场各方面性能更好,但因为 No blocking-dense布局中,对于在近塔区何时结束 campo布局规则还存在问题,故选择数学模型更加清晰的 EB布局进行优化研究。在 EB布局中,方位间距因子 Asf和重置极限因子 Arlim是布局中的关键参数,但对于有二者的取值并未有过详细研究,故选择结合实例以及优化算法探究两种参数如何取值时可以获得性能更优的定日镜场。
为验证镜场优化结果的可行性,还需利用工程实例与之进行比较和分析,因Gemasolar电站各方面的资料信息更加详实,故选择该电站作为参考。Gemasolar电站建于西班牙的塞维利亚,该镜场共由 2650面定日镜构成,其占地面积共 185英亩(约 74,86公顷),据相关资料表明镜场在 2012到 2014年的年均效率分别为 52.8589%、51.7604%、49.563%,且其最内部镜环距离吸热塔 79.96米(镜场其余相关数据见表 2.1)
为验证镜场优化结果的可行性,还需利用工程实例与之进行比较和分析,因Gemasolar电站各方面的资料信息更加详实,故选择该电站作为参考。Gemasolar电站建于西班牙的塞维利亚,该镜场共由 2650面定日镜构成,其占地面积共 185英亩(约 74,86公顷),据相关资料表明镜场在 2012到 2014年的年均效率分别为 52.8589%、51.7604%、49.563%,且其最内部镜环距离吸热塔 79.96米(镜场其余相关数据见表 2.1)。
5.1.2目标函数分析
现需结合 EB布局模式与 Gemasoalr电站的相关参数,应用混合策略鲸鱼优化算法,分别以所得镜场年均效率最高构建单目标优化问题、以所得镜场的年均效率更高以及镜场占地面积更小为目标构建双目标优化问题,对 EB布局中的关键参数进行优化。在求解定日镜场的光学效率时,因为太阳位置时刻都会发生变化,实际上所求解出的效率为当前时间下镜场的瞬时光学效率。因效率求解计算量很大,故无法对一年中所有的时间点对应的效率进行计算,故通常都会选用“典型日求平均法”所求解的效率来表示年均效率。该方法是指求解春分日、夏至日、秋分日、冬至日这四个特殊日期下的镜场效率加以平均。因为定日镜场工作的开场时间要求该时间所对应的太阳高度角必须要高于 15°,所以首先通过应用已经十分成熟的 SPA算法(太阳高度角和方位角计算算法)来求解镜场的工作时间点,在该方法中,只需要输入时间信息、经纬度坐标、海拔、温度、湿度等信息即可得到相应时间下该位置的镜场所对应的太阳高度角和方位角。通过 SPA算法求解出各个典型日的开场工作时间段后,选择区间内的整点时间进行后续的效率计算。具体时间点及所对应的太阳高度角、方位角信息如表 5.1所示。
 “典型日平均法”求解年均效率计算公式如下:
“典型日平均法”求解年均效率计算公式如下:
文章来源地址https://www.toymoban.com/news/detail-705030.html





5.2优化设计
在对定日镜场进行优化的过程中,有两个方面十分关键。一是如何根据 EB布局的数学模型生成镜场,二是如何实现算法流程,故还需对这两部分进行详细说明。
5.2.1 EB镜场生成
对于 EB布局,其基础数学模型已经十分清晰,但在结合无遮挡思想确定径向间距的过程中,发现不同的太阳高度角下根据前排定日镜数据所确定出的径向间距也有所不同。因此,通常在设计镜场前,会给定一个设计参考点,一般会选择太阳高度角为 90°、太阳方位角为 0°作为参考点,即太阳在该方位时,处于吸热塔正上方。同时,为方便计算和求解,规定在生成的 EB镜场中定日镜的中心点坐标的 z值均为 0。
在生成的定日镜场中,每一个等价圆表示一面定日镜,圆心为定日镜的中心点,而其直径为定日镜的对角线长度,其主要表示了定日镜在水平方向放置时,旋转所构成的平面范围。

在生成 EB镜场的过程中,最主要的就是如何确定方位间距和径向间距,以及何时启用无遮挡规则、何时结束镜场某一区域的布置开始布局新区域,具体布局流程如图 5.4所示。

5.2.2算法求解流程
混合策略鲸鱼优化算法对 EB布局定日镜场求解流程如下:
(1)stpe1:输入数据,包括定日镜、塔高、吸热器的相关参数、最小镜环半径、
模拟时间点对应的太阳高度角、方位角信息。
(2)step2:对控制变量编码,以方位间距因子 Asf和极限重置因子 Arlim作为算法
的个体。
(3)step3:对种群初始化,进化代数 t=0。
(4)step4:计算目标函数,同时选择出领导个体的候选部分(多目标优化问题中
通过非支配排序以及拥挤度计算)。
(5)step5:进行位置更新以及变异并计算对应的目标函数。
(6)step6:将旧种群、新种群、变异个体一起进行非支配排序后,保留精英粒子
作为此次迭代的结果,并更新全局最优解集。
(7)step7:判断 t是否大于等于 tmax,若是进行 step9,若否则进行 step9。
(8)step8:进行迭代,t=t+1,转到 step4。
(9)step9:输出最优解(或 Pareto最优解集)以及对应的个体信息,结束算法。
5.3优化结果及分析
5.3.1单目标优化
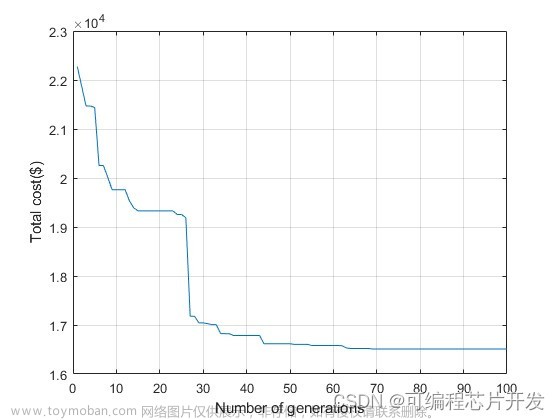
在定日镜场优化过程中,只考虑前 2650面定日镜的年均效率作为适应度函数对镜场进行优化布置。设置种群大小 N=50(即对应 50种镜场布局方案),迭代次数 t=200,结合 MSWOA算法和 WOA算法进行优化求解,并让两种算法分别运行 30此以排除偶然性结果,选择其中最优的一组数据绘制迭代曲线。
算法迭代曲线如图 5.5所示,从图中可以发现 MSWOA算法的寻优结果要高于 WOA算法,且在收敛速度上,MSWOA算法在约 140代左右开始收敛,而 WOA算法在 185代左右才收敛。从最终结果来看,采用 EB布局时,最高效率的前 2650面定日镜所组成的镜场其年均效率在 63.79%,远高于文献中所记录的 Gemasolar电站在 2012-2014年中的 52.8589%、51.7604%、49.563%,且该布局所对应的方位间距因子和极限重置因子分别为 1.65和 1.32。
为清晰展示算法迭代求解所得关键参数对应的完整镜场及高效镜场,分别绘制效率云图,利用颜色渐变来说明镜场中的效率分布,如图 5.6所示。在完整镜场中,定日镜可达到的最高效率为 77.6%,最低效率为 26.09%,按效率由高到低排列,第 2650面定日镜的效率为 50.24%。从图中,可发现镜场效率云图近似于以南北轴线对称,这是因为镜场排布时即以南北轴线对称布置,且工作时间范围内,方位角与高度角也会关于当天内最高太阳高度角对称(可表 5.1数据简单验证);镜场北部的定日镜较南部相比光学效率更高;离吸热塔越近的区域定日镜效率越高。


5.3.2多目标优化
在定日镜场优化过程中,只考虑效率最高的前 2650面定日镜,以其年均效率损失和与工程实例电站面积之比为适应度函数,对镜场进行优化布置。设置种群大小 N=50(即对应 50种镜场布局方案),迭代次数 t=200,结合多目标 MSWOA算法和多目标WOA算法进行优化求解,并让两种算法分别运行 30此以排除偶然性结果,绘制迭代结束时所得的帕累托最优解集。Pareto最优解集如图 5.7所示,从图中可以看出,MSWOA算法的 Pareto最优解集远好于 WOA算法所的的 Pareto解集,因为在 WOA算法所得结果中对于 f2函数值在1.18以后的大部分 Pareto最优解可以被 MSWOA算法所得的 Pareto最优解支配,且MSWOA算法所得结果的范围更大,说明在相同的迭代次数下算法对个体空间的探索更加深入。因 Pareto最优解集中个体较多,故分别选择 f1、f2最大值附近解以及靠近中部的部分解进行数据说明。见表 5.2。

因在工程实例 Gemasolar电站中,其占地面积约为 74.86公顷,为尽可能地在占地面积方面贴近实例数据,故选择对目标函数 2(面积比)中最小数值所对应的数据进行分析。从图中,可以发现该数据点即为表 5.2中的第一项数据,根据该布局所求的完整镜场包括了 7921面定日镜,而个体效率最高前 2650面定日镜的年均效率为 59.26%,远高于文献中所记录的 Gemasolar电站在 2012-2014年中的年均效率 52.8589%、51.7604%、49.563%,同时其占地面积略高于工程数据,为 79.1503公顷。为详细展现 该布局的模式及前 2650面定日镜的平面分布和效率分布情况,在完整镜场中将前 2650面定日镜按其效率高低,分别用不同颜色填充其等价圆绘制效率云图,如图 5.8所示。从图中,我们也可以发现,单目标镜场优化问题所得效率云图中关于定日镜效率分布的结论在此处依然适用。

 文章来源:https://www.toymoban.com/news/detail-705030.html
文章来源:https://www.toymoban.com/news/detail-705030.html
到了这里,关于基于多目标混合策略鲸鱼优化算法的镜场布局优化-2023国赛数学建模A题第三问解题思路 - 定日镜场的优化设计(详细过程,小白读完就会)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!