粒子群算法及其MATLAB实现(附完整代码和讲解)

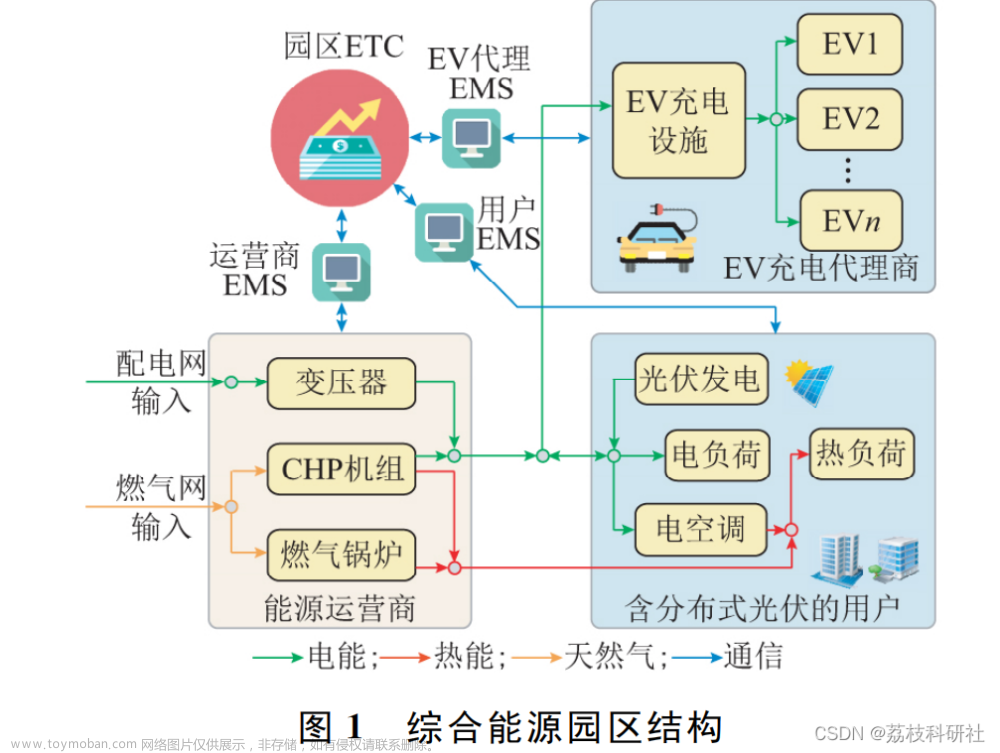
粒子群算法是模仿鸟类捕食的一种智能仿生算法，具有流程简单，算子复杂度低的特点，是一种常用的智能算法，特别适用于自变量为实数的问题优化模型,维数较多时具有很好的效率，比fmincon之类的确定性算法具有更快的速度，在有限的时间内可以获得较好的结果。

粒子群算法的核心是通过用粒子在多维空间的坐标来映射问题优化模型的解，通过粒子的当前位置、历史最优位置、种群的历史最优位置、均匀分布随机适量， 经过不同权重的组合，得到粒子下一代的位置，依此不断迭代得到近似最优解。

粒子群算法的主要流程如下图所示：

粒子群算法的两个核心公式如下：

(1)粒子的速度更新公式:

(2)粒子的位置更新公式:

其中：

vidk是第i个粒子在第d维的速度值

xidk是第i个粒子第d维第k代的位置

pidk为第i个粒子第d维的第k代的个体最优位置。

gdk为粒子群第d维的第k代的全局最优位置。

w为惯性权重, 即保持原来速度的系数。

c1是粒子跟踪自己历史最优值的权重系数，它代表的是粒子对自身的知识的认知数值,也可以称为自我认知值。通常设置为2。

c2是粒子对群体最优值的权重系数，它表示粒子对整个群体知识的认识，也可以称为社会认知值。通常设置为2

ξ和η是[0,1]区间内均匀分布的随机数，赋予粒子方向变化以随机性。

下面我们给出用MATLAB编程求解如下待优化的目标函数的代码：

程序结果如下：

主程序代码main.m如下：

%% 清空环境
clc;clear all;close all;warning off;%关闭警报
rand('seed', 100);
randn('seed', 100);
format long g;


%% 设置算法参数
popsize_my=50;% 粒子数
maxgen_my=100;% 迭代次数
dimension_my=10;% 粒子维度数

c1_my=1.8;% 速度更新参数1
c2_my=1.7;% 速度更新参数2
wMax_my=0.95;% 惯性权重最大值
wMin_my=0.85;% 惯性权重最小值


%% 设置变量区间
lb_my=0*ones(1,dimension_my);
ub_my=1*ones(1,dimension_my);

%% 设置速度的区间
vlb_my=(ub_my-lb_my)*-0.15;
vub_my=(ub_my-lb_my)*0.15;

[po_my,V]=genfun_my(popsize_my,dimension_my,lb_my,ub_my,vlb_my,vub_my);% 初始化
Va_pso_my=ddpso_my(po_my,popsize_my);% 计算目标值

%% 初始化全局最优值
[bestValue_pso_my,bestindex_pso_my]=min(Va_pso_my);
pbest_my=po_my(bestindex_pso_my,:);% 全局最优值
gb_my=po_my;% 最优个体
Vgb_my=Va_pso_my;% 个体最优值
Vb_my=bestValue_pso_my;% 全局最优值

tic;
mat_pso_my=zeros(maxgen_my,2);%
for i=1:maxgen_my
    w=wMax_my-i*(wMax_my-wMin_my)./maxgen_my;% w为惯性权重
    
    for j=1:popsize_my
        %% 速度更新
        V(j,:) = w*V(j,:) + c1_my*rand*(gb_my(j,:) - po_my(j,:)) + c2_my*rand*(pbest_my - po_my(j,:));% 速度更新
        V(j,:)=lipeedfun(V(j,:),vlb_my,vub_my,dimension_my);% 限制速度
        
        %% 粒子更新
        po_my(j,:)=po_my(j,:)+V(j,:);%更新种群
        po_my(j,:)=limitfun_my(po_my(j,:),lb_my,ub_my);
    end
    
    Va_pso_my=ddpso_my(po_my,popsize_my);%从新计算适应度值
    
    for j=1:popsize_my
        % 计算个体最优更新
        if Va_pso_my(j) < Vgb_my(j)
            gb_my(j,:) = po_my(j,:);
            Vgb_my(j) = Va_pso_my(j);
        end
        % 计算群体最优
        if Va_pso_my(j) < Vb_my
            pbest_my = po_my(j,:);
            Vb_my = Va_pso_my(j);
        end
    end
    mat_pso_my(i,1)=Vb_my;
    mat_pso_my(i,2)=mean(Va_pso_my);
end

%% 结果绘图、输出数据
disp('最优目标值');
Vb_my
disp('最优粒子');
pbest_my

%% 汇总迭代曲线
figure;
plot(mat_pso_my(:,1),'r-','linewidth',1.5);
hold on;
plot(mat_pso_my(:,2),'b-','linewidth',1.5);
legend({'最佳值','平均值'},'fontname','宋体');
xlabel('迭代次数','fontname','宋体');
ylabel('目标函数值','fontname','宋体');
title('粒子群算法迭代曲线','fontname','宋体');

目标函数代码myfun.m如下：

function y = myfun(x)
% 目标函数
y=sum((x-0.5).^2);

完整代码可以私信我, 或者从https://download.csdn.net/download/corn1949/87990740下载.文章来源地址https://www.toymoban.com/news/detail-705691.html

到了这里，关于粒子群算法及其MATLAB实现(附完整代码和讲解)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！