目录
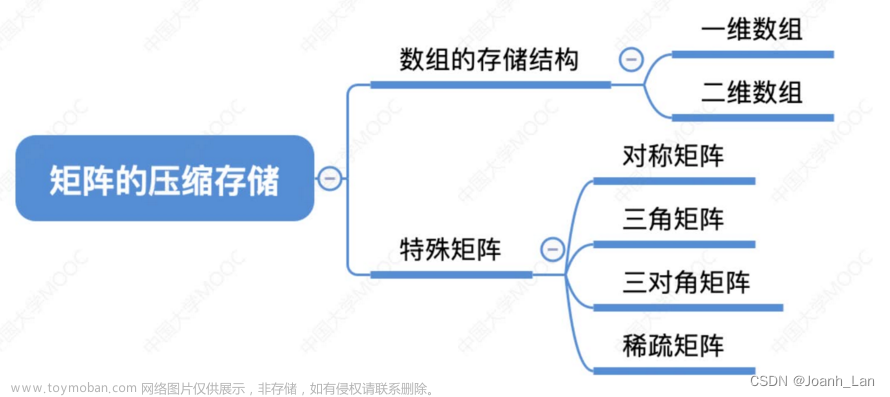
1.对阵矩阵
2.三角矩阵
3.三对角矩阵(带状矩阵)
均假设数组的下标从0开始
1.对阵矩阵
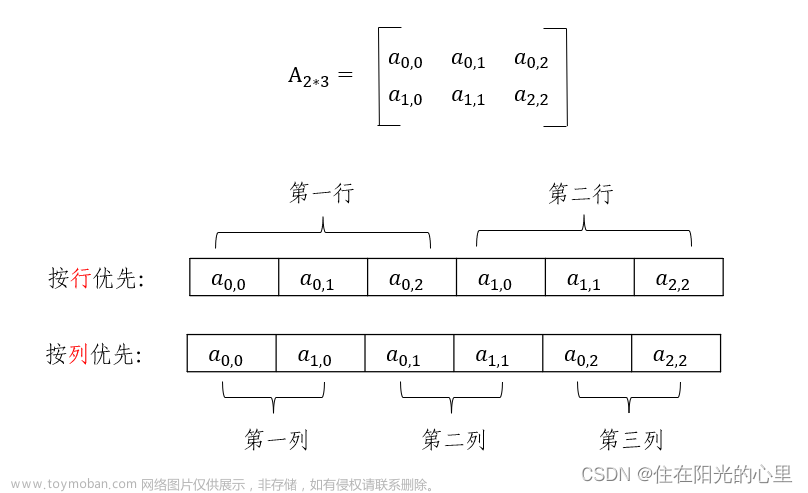
定义:若对一个n阶矩阵A中的任意一个元素 aᵢ,ⱼ 都有aᵢ,ⱼ=aⱼ,ᵢ (1≤i,j≤n),则称其为对称矩阵。

存储策略:只存储主对角线+下三角区(或主对角线+上三角区),以主对角线+下三角区为例,按照行优先把这些元素放入到一维数组中,就得到了下面的样子的一维数组:
| a₁₁ | a₂₁ | a₂₂ | a₃₁ | ... | aₙ,ₙ₋₂ | aₙ,ₙ₋₁ | aₙ,ₙ |
一维数组的大小应该定义为 (1+n)*n/2, 此公式通过求和公式,将每行元素相加即可得到。
根据性质aᵢ,ⱼ=aⱼ,ᵢ可以得到矩阵所有元素与一维数组下标k的对应关系如下:

按照行优先存储原则,aᵢ,ⱼ是第几个元素?
答:因为是行优先,所以 aᵢ,ⱼ是第 1+2+...+i-1+j 个元素,即第 i*(i-1)/2+j-1个元素。
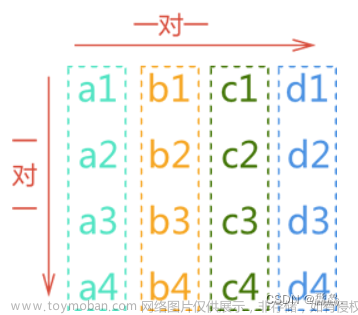
按照列优先存储原则,aᵢ,ⱼ是第几个元素?
答:因为是列优先,所以先算出前 j-1 行有多少个元素,由每列元素个数与列数 j 有关,可知每列的元素个数为 n-(j-1) 个,前 j-1 行即 n-(1-1) + n-(2-1) + n-(3-1) + ··· + n-(j-1-1)个元素,化简得前 j-1行有 n+(n-1)+...+(n-j+2) 个元素。接下来再加上第 j 行的元素,也就是 aᵢ,ⱼ 所处的那一行中, 前面的元素个数,个数为 i - j 个,综上 aᵢ,ⱼ 是第 n+(n-1)+...+(n-j+2)+(i-j)+1 个元素。
2.三角矩阵

下三角矩阵的存储思想:按行优先原则将下三角区域元素(包括主对角线元素)存入一维数组中,并在最后一个位置存储常量c。
得到一维数组:

按照行优先存储原则,aᵢ,ⱼ是第几个元素?

上三角矩阵的存储思想:按行优先原则将上三角区域元素(包括主对角线元素)存入一维数组中,并在最后一个位置存储常量c。 一维数组和下三角矩阵的一样。
按照行优先存储原则,aᵢ,ⱼ是第几个元素?

3.三对角矩阵(带状矩阵)

存储思想:按行优先或列优先原则,只存储带状部分。

矩阵中3条对角线上的元素aᵢ,ⱼ在一维数组中存放的下标为k=2i+j-3。文章来源:https://www.toymoban.com/news/detail-706778.html
反之,若已知某元素存放于一维数组B的第k个位置,则可得i的值为(k+1)/3+1向下取整(或(k+2)/3向上取整)。
文章来源地址https://www.toymoban.com/news/detail-706778.html
到了这里,关于特殊矩阵的压缩存储(对称矩阵,三角矩阵和三对角矩阵)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!