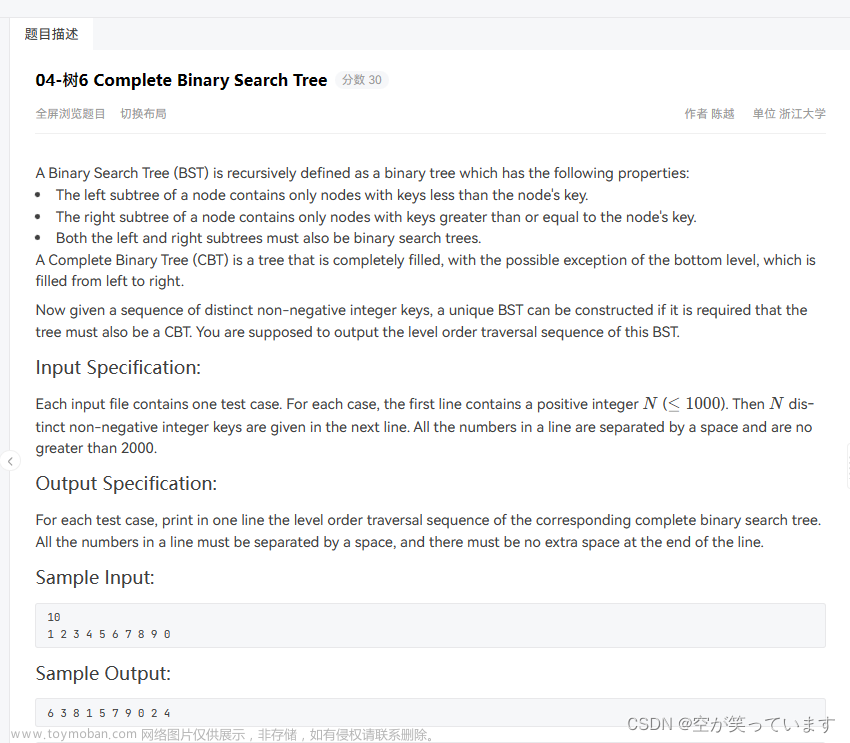
二叉搜索树(Binary Search Tree,BST)
二叉搜索树(Binary Search Tree),也称二叉查找树或二叉排序树,是一种特殊的二叉树,它满足以下性质
- 对于二叉搜索树的每个节点
- 左子树中的所有节点的值都小于该节点的值
- 右子树中的所有节点的值都大于(或等于)该节点的值
- 对于二叉搜索树的任意节点,其左子树和右子树也是二叉搜索树。

由于这种特性,二叉搜索树可以支持高效地进行查找、插入和删除操作。对于查找操作,可以通过比较目标值与当前节点的值来决定向左子树还是右子树进行搜索。对于插入操作,可以按照比较结果找到合适的位置并插入新节点。对于删除操作,则需要按照一定规则来处理不同情况下的节点删除
插入节点
在二叉搜索树中插入一个新节点的步骤如下:
- 如果树为空,将新节点作为根节点。
- 如果树不为空,从根节点开始遍历树。
- 比较要插入的值与当前节点的值。
- 如果要插入的值小于当前节点的值,向左子树方向继续遍历。
- 如果要插入的值大于当前节点的值,向右子树方向继续遍历。
- 如果要插入的值等于当前节点的值,根据具体需求决定是替换当前节点的值还是忽略该值。
- 当遇到空节点时,表示找到了合适的位置插入新节点。
- 创建一个新节点,并将其插入到空节点的位置。
- 完成插入操作。
示例代码:
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
private TreeNode root;
public BinarySearchTree() {
root = null;
}
// 插入节点
public void insert(int val) {
root = insertNode(root, val);
}
private TreeNode insertNode(TreeNode root, int val) {
// 如果当前节点为空,说明找到了应该插入的位置,创建新节点并返回
if (root == null) {
return new TreeNode(val);
}
// 如果插入的值小于当前节点的值,向左子树插入
if (val < root.val) {
root.left = insertNode(root.left, val);
} else if (val > root.val) {
// 如果插入的值大于当前节点的值,向右子树插入
root.right = insertNode(root.right, val);
}
return root;
}
}
搜索节点(查找)
在二叉搜索树中搜索一个特定值的步骤如下:文章来源:https://www.toymoban.com/news/detail-707861.html
- 从根节点开始,将要搜索的值与当前节点的值进行比较。
- 如果要搜索的值等于当前节点的值,返回true,表示找到了目标值。
- 如果要搜索的值小于当前节点的值,则向左子树方向继续搜索。
- 如果要搜索的值大于当前节点的值,则向右子树方向继续搜索。
- 如果遇到空节点,则表示未找到目标值,返回false。
- 重复步骤2至步骤5,直到找到目标值或搜索完整个树。
下面是使用上述步骤实现搜索方法的示例代码:
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
// 搜索节点
public boolean search(int val) {
return searchNode(root, val);
}
private boolean searchNode(TreeNode root, int val) {
// 当前节点为空,未找到目标值
if (root == null) {
return false;
}
// 目标值与当前节点的值相等,找到目标值
if (val == root.val) {
return true;
} else if (val < root.val) {
// 目标值小于当前节点的值,在左子树中继续搜索
return searchNode(root.left, val);
} else {
// 目标值大于当前节点的值,在右子树中继续搜索
return searchNode(root.right, val);
}
}
}
删除节点
在二叉搜索树中删除一个节点的步骤如下:文章来源地址https://www.toymoban.com/news/detail-707861.html
- 从根节点开始,找到要删除的节点。
- 如果要删除的值等于当前节点的值,根据下面不同的情况进行处理:
a. 若该节点为叶节点(没有子节点),直接删除该节点。
b. 若该节点只有一个子节点,将其子节点替代该节点的位置。
c. 若该节点有两个子节点,找到右子树中最小的节点(或左子树中最大的节点),将该节点的值替代要删除的节点的值,然后递归删除该最小节点(或最大节点)。 - 如果要删除的值小于当前节点的值,则向左子树方向继续搜索。
- 如果要删除的值大于当前节点的值,则向右子树方向继续搜索。
- 当遇到空节点时,表示未找到要删除的节点。
- 完成删除操作。
下面是使用上述步骤实现删除方法的示例代码:
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
private TreeNode deleteNode(TreeNode root, int val) {
// 当前节点为空,未找到要删除的节点
if (root == null) {
return null;
}
// 如果要删除的值小于当前节点的值,在左子树中继续搜索
if (val < root.val) {
root.left = deleteNode(root.left, val);
} else if (val > root.val) {
// 如果要删除的值大于当前节点的值,在右子树中继续搜索
root.right = deleteNode(root.right, val);
} else {
// 找到要删除的节点
// 情况1: 当节点没有子节点时,直接返回 null
if (root.left == null && root.right == null) {
return null;
}
// 情况2: 当节点只有一个子节点时,返回子节点作为当前节点的替代
if (root.left == null) {
return root.right;
} else if (root.right == null) {
return root.left;
}
// 情况3: 当节点有两个子节点时,找到右子树中最小的节点,
// 用该节点的值替代当前节点的值,并删除右子树中最小的节点
TreeNode successor = findMin(root.right);
root.val = successor.val;
root.right = deleteNode(root.right, successor.val);
}
return root;
}
private TreeNode findMin(TreeNode node) {
while (node.left != null) {
node = node.left;
}
return node;
}
}
到了这里,关于二叉搜索树(Binary Search Tree,BST)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!