1. Toy模板网首页
  2. > Toy博客

【数据结构】AVL树的插入与验证

10月前 作者：舜华丶 分类：Toy博客 阅读(36) 违法举报

这篇具有很好参考价值的文章主要介绍了【数据结构】AVL树的插入与验证。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

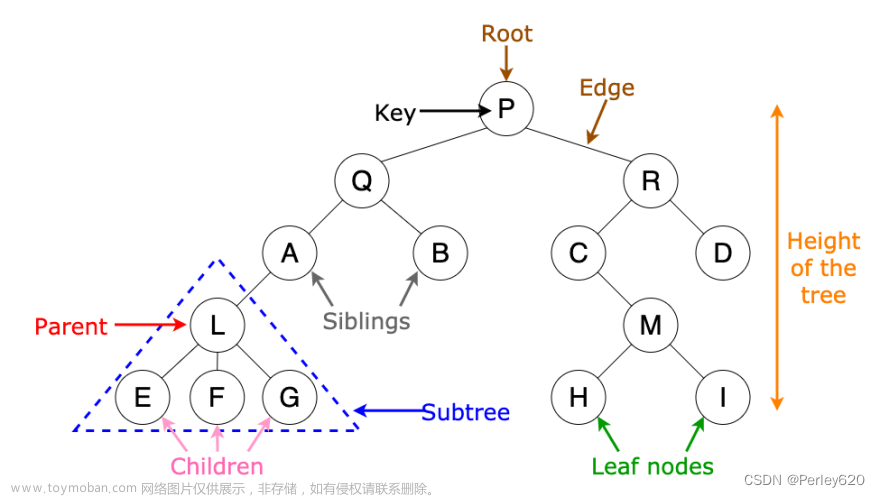
一、基本概念

1.发展背景

  • 普通的二叉搜索树在极端情况下会退化成类似链表的形状，从而使查找的效率降低至O(N)。

  • 在此基础上，苏联与以色列数学家Adelson-Velskii 与 苏联数学家Landis，发明出了 AVL树或者说平衡二叉搜索树。

【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++
【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++

注：第一张——Adelson-Velskii（1922-2014） ，第二张——Landis（1921——1997）

2.性质

  • 左右子树的高度差的绝对值不大于1
  • 每个子树都是AVL树。

说明：这样做的目的就是为了严格控制平衡，以便于提高查找效率，但是控制高度差一直为0是不可能的，至于为什么不能控制成0，假设只有两个结点必然存在1的高度差。

二、实现原理

①插入操作

1.平衡因子

英文名：balance factor

  • 目的：保证左右子树的高度差的绝对值不大于1
  • 大多数的实现方式：存放的是右子树与左子树的高度差
1.1平衡因子的更新
1.1.1树的高度变化

① 左边新增结点
【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++

② 右边新增结点

【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++

  • 总结
  1. 左边新增，根节点的平衡因子减1
  2. 右边新增，根节点的平衡因子加1
  3. 平衡因子从0变为1或者-1

继续分析：
 两种情况树的高度增加1，也就是平衡因子从0变为1或者-1，既然高度变化了，可能会导致上面的树不平衡。
如：
【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++

此时我们需要向上更新平衡因子，再根据右边高度变化与左边高度变化，决定根的平衡因子加1还是减1。

  • 推论：由于可能会向上更新平衡因子，那么AVL树是三叉链的结构。

如图：
【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++

1.1.2树的高度不变

① 左边新增结点

【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++
② 右边新增结点

【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++

  • 同理
  1. 左边新增，根节点的平衡因子减1
  2. 右边新增，根节点的平衡因子加1
  3. 平衡因子由1或者-1变为0

继续分析，这里的根节点的所在树的高度即——左右子树高度的最大值 + 1（根节点的高度）

左右子树的高度的最大值不变，即这颗树高度不变，即不用往上继续更新且达到平衡。

2. 旋转

  • 说明：旋转就是让不平衡的树再次平衡的手段。

  • 条件：平衡因子为2或者-2，即高度差的绝对值为2。

  • 补充：若平衡因子大于等于3，说明当前树就不是AVL树，需要检验之前的代码。

但是我们又得对情况进行分类讨论，因为不同情况让树再次平衡的旋转方式不同。

2.1左旋
  • 说明：也就是右边高度高，需要旋转来降低右边的高度，进而达到平衡。

一步一步分析，先来个最简单的：

【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++
此时，旋转过后平衡因子全变为0，且当前树达到平衡。注意此时3结点的左结点为空！(细节)

再举一个例子：

【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++

此时，旋转过后平衡因子1和3的平衡因子变为0，且当前树达到平衡，此时我们是不用管其它子树的，因为子树必然是AVL树，要不然更不到根节点就停止了。

最后来一个稍微复杂的例子：
【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++
此时，旋转过后平衡因子-5和0的平衡因子变为0，且当前树达到平衡。

这是具体的图便于辅助理解，然后我们再画出所有情况的抽象图：
【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++

  • 总结
  1. 只能在c部分上插入结点才可能会引发根节点左单旋,也就是说parent的右边为cur且新增结点在cur的右边。
  2. 旋转过后cur与parent的平衡因子变为0。
  • 细节
  1. b的父节点连接parent时，需要判断b部分是否为空。
  2. parent的父节点连接cur时，需要保存一下parent的父节点。
  3. 根据parent的父节点判断是否需要修改根节点，若为空则修改，若不为空，则将cur链接到parent的父节点，同时更新parent父节点的指向。
  • 实现代码
	void RotateL(Node* parent)
	{
		//画图分析：
		//操作的结点有cur,cur_left,ppnode
		Node* cur = parent->_right;
		Node* cur_left = cur->_left;
		//将parent的右节点改为cur_left
		parent->_right = cur_left;
		//改变cur_left父节点的转向
		//cur_left可能为空
		if (cur_left != nullptr)
		{
			cur_left->_parent = parent;
		}
		//将parent链接在cur的左边
		//为了更新cur的parent需要保存parent的父节点
		Node* ppnode = parent->_parent;

		cur->_left = parent;
		parent->_parent = cur;

		//ppnode可能为空
		if (ppnode == nullptr)
		{
			//需要修改根节点
			_root = cur;
			cur->_parent = nullptr;
		}
		else
		{
			//改变ppnode的指向
			if (ppnode->_left == parent)
			{
				ppnode->_left = cur;
			}
			else
			{
				ppnode->_right = cur;
			}
			cur->_parent = ppnode;

		}

		//更新平衡因子
		cur->_bf = parent->_bf = 0;

	}
2.2右旋

说明：也就是左边高度高，需要旋转来降低右边的高度，进而达到平衡。

跟左旋的分析方式一样。

先来个简单的感受一下：

【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++

此时，旋转过后平衡因子parent和cur的平衡因子变为0，且当前树达到平衡。

再举一个例子：
【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++
最后来一个稍微复杂的例子：
【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++

画出所有情况的抽象图：

【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++

  • 总结
  1. 只能在a部分上插入结点才可能会引发根节点右单旋,也就是说parent与cur与高度变化的c树的根节点在同一个方向且在parent的左
  2. 旋转过后cur与parent的平衡因子变为0。
  • 细节——同左旋
  1. b的父节点连接parent时，需要判断b部分是否为空。
  2. parent的父节点连接cur时，需要保存一下parent的父节点。
  3. 根据parent的父节点判断是否需要修改根节点，若为空则修改，若不为空，则将cur链接到parent的父节点，同时更新parent父节点的指向。
  • 实现代码：
		void RotateR(Node* parent)
		{
			//操作的结点
			Node* cur = parent->_left;
			Node* cur_right = cur->_right;

			//第一步：将cur_right链接到parent的left
			parent->_left = cur_right;
			//更改cur_right的父节点
			//注意：cur_right可能为空
			if (cur_right != nullptr)
			{
				cur_right->_parent = parent;
			}
			//第二步：将parent链接到cur的右结点。
			//先保存一下parent的父节点
			Node* ppnode = parent->_parent;

			cur->_right = parent;
			parent->_parent = cur;
			//ppnode为空说明需要修改根节点
			if (ppnode == nullptr)
			{
				_root = cur;
				cur->_parent = nullptr;
			}
			else
			{
				if (ppnode->_left == parent)
				{
					ppnode->_left = cur;
				}
				else
				{
					ppnode->_right = cur;
				}

				cur->_parent = ppnode;
			}
			
			//更新平衡因子
			cur->_bf = parent->_bf = 0;

		}
2.3右左双旋
  • 可以简单理解为，需要进行处理的左旋。

说明：单旋无法解决问题，原因是发生了拐弯，需要用右旋讲折线变为直线，再进行左旋。

因为情况有点多我们就来个简单的，直接化抽象图，看结论比较容易理解。

先来个简单的：
【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++
先右旋之后折线变成了直线，变成了左旋的形状，再进行左旋，最后的cur与cur_left与parent的平衡因子变成了0，最终cur_left变成了根节点。

再化抽象图：

初始状态
【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++

【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++
还是一样，不过得分两种情况进行讨论：

  1. 新增结点在c树上，会导致parent的平衡因子变为-1，cur的平衡因子变为0。
  2. 新增结点在b树上，会导致parent的平衡因子变为0，cur的平衡因子变为1
  3. 不管新增结点在谁上，cur_left的平衡因子都为0。

  • 看图分析，其实不看新增结点在谁身上，两种最终的旋转的结果是一样的，那我们其实只需先不看新增结点再画图，根据最终的结果再把新增结点添上，其实会更加直观。

  • 总结

  1. 新增结点在c树上，会导致parent的平衡因子变为-1，cur的平衡因子变为0。
  2. 新增结点在b树上，会导致parent的平衡因子变为0，cur的平衡因子变为1。
  3. cur_left为新增结点，parent与cur的结点全为0。
  • 实现代码：
	void RotateRL(Node* parent)
	{
		Node* cur = parent->_right;
		Node* cur_left = cur->_left;

		//CL——CurLeft
		int CL_bf = cur_left->_bf;
		RotateR(cur);
		RotateL(parent);
		//更新平衡因子
		if (CL_bf == 0)
		{
			cur->_bf = parent->_bf = cur_left->_bf = 0;
			//虽然没必要，但是起到了解耦的作用。
		}
		else if (CL_bf == 1)
		{
			parent->_bf = -1;
			cur->_bf = cur_left->_bf = 0;
		}
		else if(CL_bf == -1)
		{
			cur->_bf = 1;
			parent->_bf = cur_left->_bf = 0;
		}
		else
		{
			cout << __LINE__ << ":" << endl;
			perror("平衡因子有误");
			exit(-1);
		}
	}
2.4 左右双旋
  • 可以理解为，需要进行处理的右旋。

说明：单旋无法解决问题，原因是发生了拐弯，需要用左旋讲折线变为直线，再进行右旋。

分析方法跟右左双旋一样。

先来个简单的：

【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++
先左旋之后折线变成了直线，变成了右旋的形状，再进行右旋，最后的cur与cur_left与parent的平衡因子变成了0，最终cur_left变成了根节点。

再来个抽象的：
【数据结构】AVL树的插入与验证,数据结构,数据结构,AVL树,c++
还是一样，不过得分两种情况进行讨论：

  1. 新增结点在c树上，会导致cur的平衡因子变为-1，parent的平衡因子变为0。
  2. 新增结点在b树上，会导致cur的平衡因子变为0，parent的平衡因子变为1
  3. 不管新增结点在谁上，cur_right的平衡因子都为0。
  • 总结
  1. cur_right平衡因子为1，说明新增结点在b树上，会导致cur的平衡因子变为0，parent的平衡因子变为1。
  2. cur_right的平衡因子为-1，新增结点在c树上，会导致cur的平衡因子变为-1，parent的平衡因子变为0。
  3. cur_right的平衡因子为0，cur与parent的平衡因子都变为0。
  4. 不管新增结点在谁上，cur_right的平衡因子都为0。
  • 代码实现
		void RotateLR(Node* parent)
		{
			Node* cur = parent->_left;
			Node* cur_right = cur->_right;
			int CR_bf = cur_right->_bf;

			RotateL(cur);
			RotateR(parent);

			if (CR_bf == 0)
			{
				parent->_bf = cur->_bf = cur_right->_bf = 0;
			}
			else if(CR_bf == 1)
			{
				cur->_bf = -1;
				parent->_bf = cur_right->_bf = 0;
			}
			else if (CR_bf == -1)
			{
				parent->_bf = 1;
				cur->_bf = cur_right->_bf = 0;
			}
			else
			{
				cout << __LINE__ << ":" << endl;
				perror("平衡因子有误");
				exit(-1);
			}
		}

②验证

说明：

  1. 根据定义验证每颗子树的高度差
  2. 需要判断当前的右子树的高度差是否等于平衡因子

直接根据平衡因子进行判断，有点监守自盗的感觉，你能保证自己更新的平衡因子就是正确的么？我都不敢保证。

1.求二叉树高度

  • 后序遍历
	size_t Height(Node* root)
	{
		if (root == nullptr)
		{
			return 0;
		}

		int LHeight = Height(root->_left);
		int RHeight = Height(root->_right);


		return max(LHeight, RHeight) + 1;
	}

2. 判断是否为AVL树

	bool _IsAVLTree(Node* root)
	{
		if (root == nullptr)
		{
			return true;
		}
		int RHeight = Height(root->_right);
		int LHeight = Height(root->_left);

		if (abs(RHeight - LHeight) > 1 || root->_bf != RHeight - LHeight)
		{
			return false;
		}

		return _IsAVLTree(root->_left) && _IsAVLTree(root->_right);
	}

优化一下：

	bool IsAVLTree()
	{
		bool is_AVL = true;
		_IsAVLTree(_root, is_AVL);

		return is_AVL;
	}

	int _IsAVLTree(Node* root,bool& is_AVL)
	{
		if (root == nullptr)
		{
			return 0;
		}
		int RHeight = _IsAVLTree(root->_right, is_AVL);
		int LHeight = _IsAVLTree(root->_left, is_AVL);

		if (abs(RHeight - LHeight) > 1 || root->_bf != RHeight - LHeight)
		{
			is_AVL = false;
		}
		return max(RHeight, LHeight) + 1;
	}

源码

#include<iostream>
#include<assert.h>
using namespace std;
namespace MY_STL
{
	template<class Key,class Val>
	struct  AVLTreeNode
	{
		typedef AVLTreeNode<Key, Val> Node;
		AVLTreeNode(const pair<Key,Val>& key = pair<Key,Val>())
			:_key(key.first)
			,_val(key.second)
			,_left(nullptr)
			,_right(nullptr)
			,_parent(nullptr)
			,_bf(0)
		{}

		Key _key;
		Val _val;
		//三叉链的结构
		Node* _left;
		Node* _right;
		Node* _parent;
		int _bf;
	};
	template<class Key, class Val>
	class AVLTree
	{
		typedef AVLTreeNode<Key, Val> Node;
	public:
		AVLTree()
		{}

		bool insert(const pair<Key,Val>& val)
		{
			//第一步：插入操作
			//如果根节点为空
			if (_root == nullptr)
			{
				_root = new Node(val);
				return true;
			}
			else
			{
				Node* cur = _root,*parent = _root;
				while (cur)
				{
					if (cur->_key > val.first)
					{
						parent = cur;
						cur = cur->_left;

					}
					else if(cur->_key < val.first)
					{
						parent = cur;
						cur = cur->_right;

					}
					else
					{
						return false;
					}
				}
				cur = new Node(val);
				if (parent->_key > val.first)
				{
					parent->_left = cur;
				}
				else
				{
					parent->_right = cur;
				}
				//更新新增结点的_parent
				cur->_parent = parent;

				//第二步：更新平衡因子
				//平衡因子：
				//1. 定义为右子树的高度减去左子树的高度
				//2. 合法范围为{-1,0,1}
				//3. 新增结点在左，父节点的平衡因子减1
				//4. 新增结点在右，父节点的平衡因子加1
				//5. 当父节点的平衡因子变为0——由-1变0或者1变0时，此时AVL树的高度不变
				//6. 当父节点的平衡因子变为1或者-1，AVL子树的高度变化，继续向上变化。
				//7. 当父节点的平衡因子变为2或者-2时，此时需要旋转，进行平衡
				//8. 当父节点为根节点时，此时需要结束循环。

				while (cur != _root)
				{
					//更新平衡因子
					if (parent->_left == cur)
					{
						//左减1
						(parent->_bf)--;
					}
					else
					{
						//右加1
						(parent->_bf)++;
					}
					//判断平衡因子
					if (parent->_bf == 0)
					{
						break;
					}
					else if (parent->_bf == 1 || parent->_bf == -1)
					{
						cur = parent;
						parent = cur->_parent;
					}
					else if (parent->_bf == 2 || parent->_bf == -2)
					{
						//对旋转进行分类讨论
						//if (parent->_bf == 2 && cur->_bf == 1)
						//{
						//	//左单旋
						//	RotateL(parent);
						//}
						//else if (parent->_bf == -2 && cur->_bf = -1)
						//{
						//	//右单旋
						//	RotateR(parent);
						//}
						//else if (parent->_bf == 2 && cur->_bf == -1)
						//{
						//	RotateRL(parent);
						//}
						//else if (parent->_bf == -2 && cur->_bf == 1)
						//{
						//	RotateLR(parent);
						//}
						if (parent->_bf == 2)
						{
							//左单旋
							if (cur->_bf == 1)
							{
								RotateL(parent);
							}
							else
							{
								RotateRL(parent);
							}
						}
						else
						{
							//右单旋
							if (cur->_bf == -1)
							{
								RotateR(parent);
							}
							else
							{
								RotateLR(parent);
							}
						}
						
						//旋转完成，树达到平衡
						break;
					}
				}
				

				return true;
			}
		}
		//根据定义进行判断
		bool IsAVLTree()
		{
			bool is_AVL = true;
			_IsAVLTree(_root, is_AVL);

			return is_AVL;

			//return _IsAVLTree(_root);
		}

		void Print()
		{
			_InOrder(_root);
			cout << endl;
		}
		//根据平衡因子进行判断
		//bool IsAVLTree()
		//{
		//	return _IsAVLTree(_root);
		//}

	private:
		void _InOrder(Node* root)
		{
			if (root == nullptr)
			{
				return;
			}
			_InOrder(root->_left);
			cout << root->_key << " ";
			_InOrder(root->_right);
		}
		//bool _IsAVLTree(Node* root)
		//{
		//	if (root == nullptr)
		//		return true;
		//	if (root->_bf >= 2 || root->_bf <= -2)
		//	{
		//		return false;
		//	}
		//	else
		//	{
		//		return _IsAVLTree(root->_left) && _IsAVLTree(root->_right);
		//	}
		//}

		//bool IsAVLTree()
		//{
		//	bool is_AVL = true;
		//	_IsAVLTree(_root, is_AVL);

		//	return is_AVL;
		//}

		size_t Height(Node* root)
		{
			if (root == nullptr)
			{
				return 0;
			}

			int LHeight = Height(root->_left);
			int RHeight = Height(root->_right);


			return max(LHeight, RHeight) + 1;
		}
		int _IsAVLTree(Node* root,bool& is_AVL)
		{
			if (root == nullptr)
			{
				return 0;
			}
			int RHeight = _IsAVLTree(root->_right, is_AVL);
			int LHeight = _IsAVLTree(root->_left, is_AVL);

			if (abs(RHeight - LHeight) > 1 || root->_bf != RHeight - LHeight)
			{
				is_AVL = false;
			}
			return max(RHeight, LHeight) + 1;
		}

		bool _IsAVLTree(Node* root)
		{
			if (root == nullptr)
			{
				return true;
			}
			int RHeight = Height(root->_right);
			int LHeight = Height(root->_left);

			if (abs(RHeight - LHeight) > 1 || root->_bf != RHeight - LHeight)
			{
				return false;
			}

			return _IsAVLTree(root->_left) && _IsAVLTree(root->_right);
		}

		void RotateLR(Node* parent)
		{
			Node* cur = parent->_left;
			Node* cur_right = cur->_right;
			int CR_bf = cur_right->_bf;

			RotateL(cur);
			RotateR(parent);

			if (CR_bf == 0)
			{
				parent->_bf = cur->_bf = cur_right->_bf = 0;
			}
			else if(CR_bf == 1)
			{
				cur->_bf = -1;
				parent->_bf = cur_right->_bf = 0;
			}
			else if (CR_bf == -1)
			{
				parent->_bf = 1;
				cur->_bf = cur_right->_bf = 0;
			}
			else
			{
				cout << __LINE__ << ":" << endl;
				perror("平衡因子有误");
				exit(-1);
			}
		}
		void RotateRL(Node* parent)
		{
			Node* cur = parent->_right;
			Node* cur_left = cur->_left;

			//CL——CurLeft
			int CL_bf = cur_left->_bf;
			RotateR(cur);
			RotateL(parent);

			if (CL_bf == 0)
			{
				cur->_bf = parent->_bf = cur_left->_bf = 0;
			}
			else if (CL_bf == 1)
			{
				parent->_bf = -1;
				cur->_bf = cur_left->_bf = 0;
			}
			else if(CL_bf == -1)
			{
				cur->_bf = 1;
				parent->_bf = cur_left->_bf = 0;
			}
			else
			{
				cout << __LINE__ << ":" << endl;
				perror("平衡因子有误");
				exit(-1);
			}
		}

		void RotateL(Node* parent)
		{
			//画图分析：
			//操作的结点有cur,cur_left,ppnode
			Node* cur = parent->_right;
			Node* cur_left = cur->_left;
			//将parent的右节点改为cur_left
			parent->_right = cur_left;
			//改变cur_left父节点的转向
			//cur_left可能为空
			if (cur_left != nullptr)
			{
				cur_left->_parent = parent;
			}
			//将parent链接在cur的左边
			//为了更新cur的parent需要保存parent的父节点
			Node* ppnode = parent->_parent;

			cur->_left = parent;
			parent->_parent = cur;

			//ppnode可能为空
			if (ppnode == nullptr)
			{
				//需要修改根节点
				_root = cur;
				cur->_parent = nullptr;
			}
			else
			{
				//改变ppnode的指向
				if (ppnode->_left == parent)
				{
					ppnode->_left = cur;
				}
				else
				{
					ppnode->_right = cur;
				}
				cur->_parent = ppnode;

			}

			//更新平衡因子
			cur->_bf = parent->_bf = 0;

		}
		void RotateR(Node* parent)
		{
			//操作的结点
			Node* cur = parent->_left;
			Node* cur_right = cur->_right;

			//第一步：将cur_right链接到parent的left
			parent->_left = cur_right;
			//更改cur_right的父节点
			//注意：cur_right可能为空
			if (cur_right != nullptr)
			{
				cur_right->_parent = parent;
			}
			//第二步：将parent链接到cur的右结点。
			//先保存一下parent的父节点
			Node* ppnode = parent->_parent;

			cur->_right = parent;
			parent->_parent = cur;
			//ppnode为空说明需要修改根节点
			if (ppnode == nullptr)
			{
				_root = cur;
				cur->_parent = nullptr;
			}
			else
			{
				if (ppnode->_left == parent)
				{
					ppnode->_left = cur;
				}
				else
				{
					ppnode->_right = cur;
				}

				cur->_parent = ppnode;
			}
			
			//更新平衡因子
			cur->_bf = parent->_bf = 0;

		}
		Node* _root = nullptr;
	};
};

总结

 AVL树还有删除操作，等博主有空再补充，对于AVL树一般来说只需要弄懂一种单旋，一种双旋，再加一些细写处理，代码是不难的，难就难在了分类讨论+画图上。今天的分享就到这里了，如果感觉有所帮助，不妨点个赞鼓励一下吧！文章来源地址https://www.toymoban.com/news/detail-709144.html

到了这里，关于【数据结构】AVL树的插入与验证的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • Java 数据结构篇-实现 AVL 树的核心方法

    Java 数据结构篇-实现 AVL 树的核心方法

    🔥博客主页： 【 小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍   文章目录         1.0 AVL 树的说明         2.0 AVL 树的成员变量及其构造方法         3.0 实现 AVL 树的核心方法         3.1 获取当前节点的高度 height(AVLNode node)         3.2 更新当前节点的高度 updateHe

    2024年01月23日
    浏览(47)
  • Java学数据结构（2）——树Tree & 二叉树binary tree & 二叉查找树 & AVL树 & 树的遍历

    Java学数据结构（2）——树Tree & 二叉树binary tree & 二叉查找树 & AVL树 & 树的遍历

    1.树的出现：解决链表线性访问时间太慢，树的时间复杂度O(logN)； 2.二叉树的定义，最多两个儿子节点； 3.二叉查找树，左小，右大，中居中；remove方法，两种，只有一个儿子节点，有两个儿子节点； 4.AVL树，在二叉查找树基础上加平衡条件，旋转方法，单旋转，双旋转；

    2024年02月10日
    浏览(49)
  • 数据结构之进阶二叉树（二叉搜索树和AVL树、红黑树的实现）超详细解析，附实操图和搜索二叉树的实现过程图

    数据结构之进阶二叉树（二叉搜索树和AVL树、红黑树的实现）超详细解析，附实操图和搜索二叉树的实现过程图

    绪论​ “生命有如铁砧，愈被敲打，愈能发出火花。——伽利略”；本章主要是数据结构 二叉树的进阶知识，若之前没学过二叉树建议看看这篇文章一篇掌握二叉树，本章的知识从浅到深的 对搜索二叉树的使用进行了介绍和对其底层逻辑的实现进行了讲解 ，希望能对你有所

    2024年02月04日
    浏览(47)

  • 二叉排序树的创建、插入、查找和删除【数据结构】

    若它的左子树不空，则左子树上所有结点的值均小于它根结点的值。 若它的右子树不空，则右子树上所有结点的值均大于它根结点的值。 它的左、右树又分为⼆叉排序树 二叉排序树也叫二叉查找树、二叉搜索树 题目描述 给出一个数据序列，建立二叉排序树，并实现插入功

    2024年01月24日
    浏览(44)

  • 二叉排序树的插入删除和查找(数据结构实训)(难度系数100)

    二叉排序树的插入删除和查找 pre: 前序遍历 in: 中序遍历 post：后序遍历 insert: 插入，本题中不会出现相同的元素 delete: 删除，删除成功输出TRUE,没有该元素则输出FALSE，删除的方法是如果有左子树，以左子树中最大值作为新的树根，否则，以右子树最小值作为树根。 search：

    2024年01月25日
    浏览(51)

  • C语言数据结构二叉排序树的建立、插入、删除、查找操作（原理+完整代码）

    1、若左子树不为空，左子树上所有节点值小于 它根节点的值 2、若右子树不为空，右子树上所有节点值大于 它根节点的值 3、每个节点的左右子树也是二叉排序树 目的：提高查找、插入、删除的速度（不是为了排序） 时间复杂度：由于查找性能取决于树的形态，所以

    2024年02月09日
    浏览(49)
  • 【C++】详解AVL树的旋转及其插入操作

    【C++】详解AVL树的旋转及其插入操作

    二叉搜索树虽然可以缩短查找的效率，但 如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下 。因此，两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法： 当向二叉搜索树中插入新节点后，

    2024年02月15日
    浏览(45)
  • 【C++】AVL树和红黑树的插入

    【C++】AVL树和红黑树的插入

    时间过的好快，我也修炼到红黑树了 人世这一遭，何其短暂而漫长啊…… 1. 虽然二叉搜索树的搜索效率很高，当搜索树接近满二叉树时，搜索效率可以达到logN，但是如果数据是有序的，则二叉搜索树会退化为单支树，搜索效率和普通的序列式容器相同了就，所以在搜索树的

    2023年04月08日
    浏览(45)
  • 【数据结构】AVL树

    【数据结构】AVL树

    🐱作者：一只大喵咪1201 🐱专栏：《数据结构与算法》 🔥格言： 你只管努力，剩下的交给时间！ 我们知道，二叉搜索树的搜索效率非常高，平均时间复杂度是O(log 2 N)，但是当数据原本就有序时，插入二叉树中就会形成单支结构，此时搜索的时间复杂度就是O(N)。 为了避免

    2023年04月18日
    浏览(36)
  • 【数据结构】AVL 树

    【数据结构】AVL 树

    前面对 map / multimap / set / multiset 进行了简单的介绍【C++】map set，在其文档介绍中发现，这几个容器有个共同点是： 其底层都是按照二叉搜索树来实现的 ，但是二叉搜索树有其自身的缺陷，假如往树中插入的元素有序或者接近有序，二叉搜索树就会退化成单支树，时间复杂度

    2024年04月12日
    浏览(32)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包