第一章 神经网络是如何实现的
这些年人工智能蓬勃发展，在语音识别、图像识别、自然语言处理等多个领域得到了很好的应用。推动这波人工智能浪潮的无疑是深度学习。所谓的深度学习实际上就是多层神经网络，至少到目前为止，深度学习基本上是用神经网络实现的。神经网络并不是什么新的概念，早在上个世纪40年代就开展了以感知机为代表的神经网络的研究，只是限于当时的客观条件，提出的模型比较简单，只有输入、输出两层，功能有限，连最简单的异或问题（XOR问题）都不能求解，神经网络的研究走向低潮。
到了80年代中期，随着BP算法的提出，神经网络再次引起研究热潮。当时被广泛使用的神经网络，在输入层和输出层之间引入了隐含层，不但能轻松求解异或问题，还被证明可以逼近任意连续函数。但限于计算能力和数据资源的不足，神经网络的研究再次陷入低潮。
一直对神经网络情有独钟的多伦多大学的辛顿教授，于2006年在《科学》上发表了一篇论文，提出了深度学习的概念，至此神经网络以深度学习的面貌再次出现在研究者的面前。但是深度学习并不是简单地重复以往的神经网络，而是针对以往神经网络研究中存在的问题，提出了一些解决方法，可以实现更深层次的神经网络，这也是深度学习一词的来源。
随着深度学习方法先后被应用到语音识别、图像识别中，并取得了传统方法不可比拟的性能，深度学习引起了人工智能研究的再次高潮。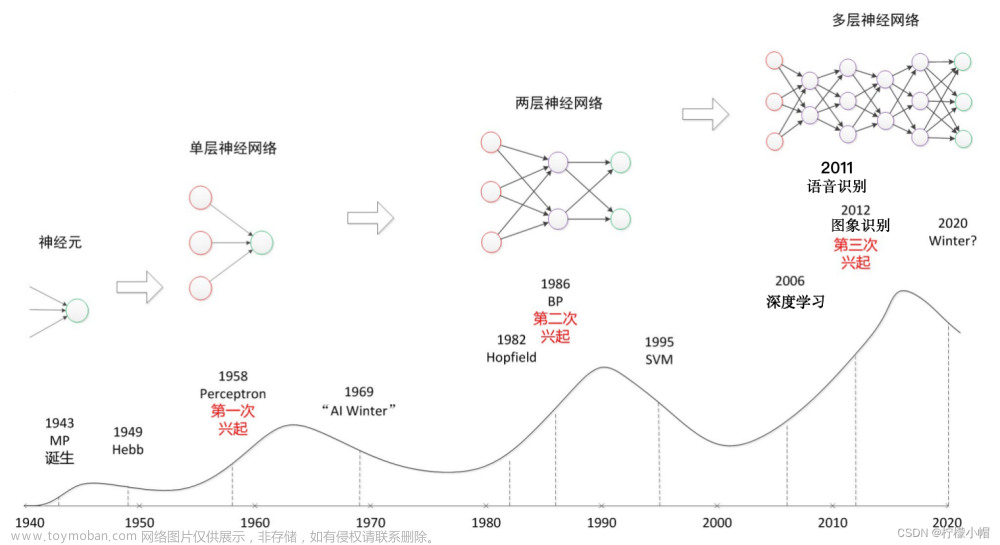
一、数字识别
1. 引入例子
- 下图是个数字3的图像，其中1代表有笔画的部分，0代表没有笔画的部分。假设想对0到9这十个数字图像进行识别，也就是说，如果任给一个数字图像，我们想让计算机识别出这个图像是数字几，我们应该如何做呢？
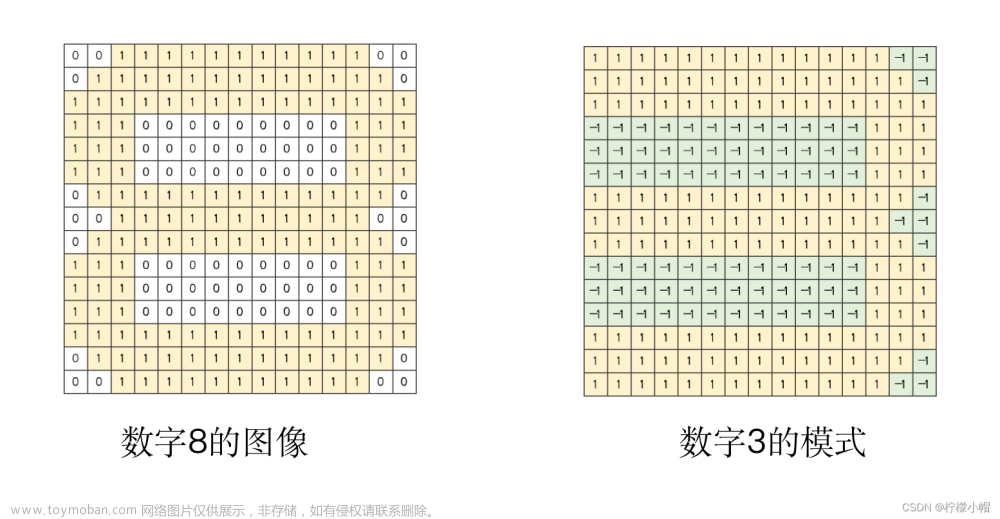
2. 模式匹配
- 一种简单的办法就是对每个数字构造一个模式，比如对数字3，我们这样构造模式：有笔画的部分用1表示，而没有笔画的部分，用-1表示，如图所示。当有一个待识别图像时，我们用待识别图像与该模式进行匹配，匹配的方法就是用图像和模式的对应位置数字相乘，然后再对相乘结果进行累加，累加的结果称为匹配值。为了方便表示，我们将模式一行一行展开用
w
i
w_i
wi(
i
i
i = 1, 2, …, n) 表示模式的每一个点。待识别图像也同样处理，用
x
i
x_i
xi(
i
i
i = 1, 2, …, n) 表示。这里假定模式和待识别图像的大小是一样的，由n个点组成。
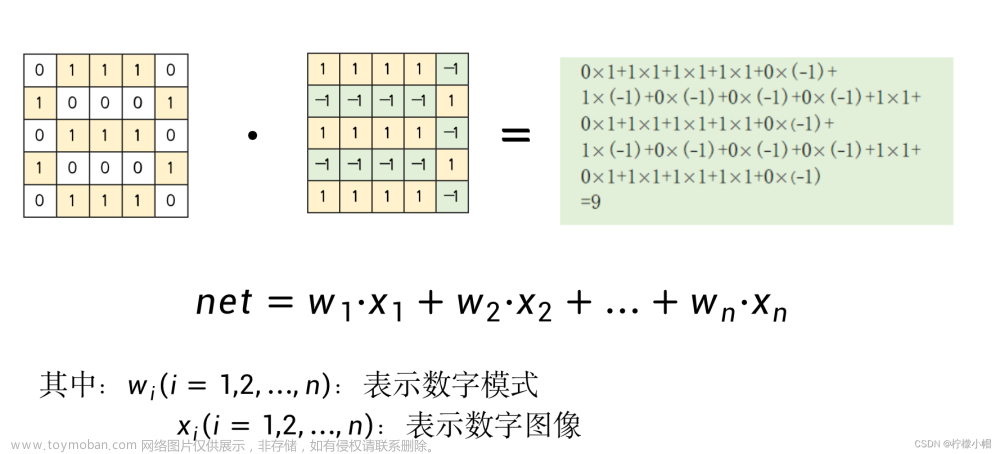
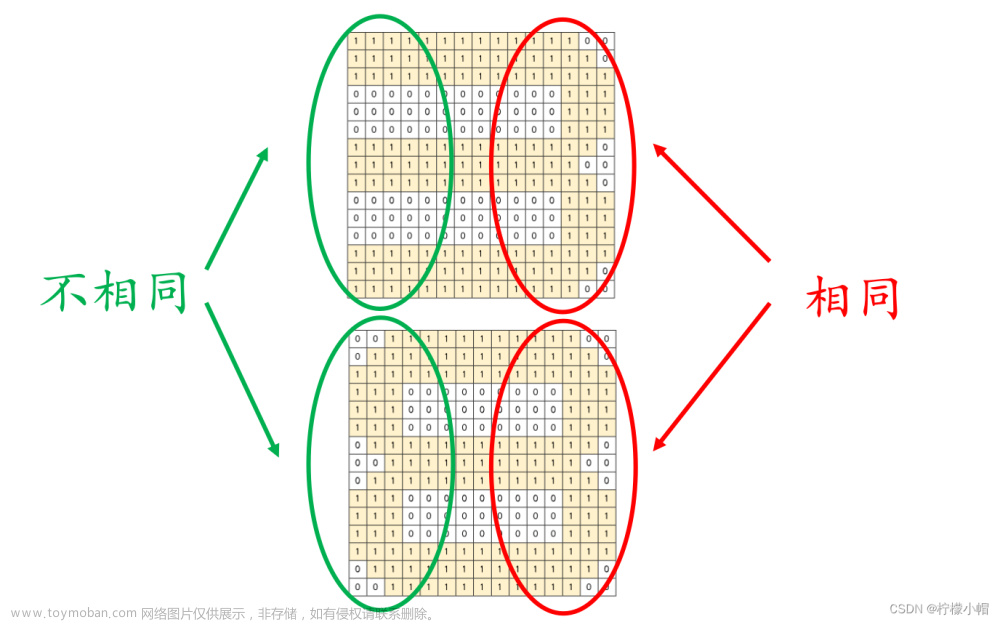
- 如果模式与待识别图像中的笔画是一样的，就会得到一个比较大的匹配结果，如果有不一致的地方，比如模式中某个位置没有笔画，这部分在模式中为-1，而待识别图像中相应位置有笔画，这部分在待识别图像中为1，这样对应位置相乘就是-1，相当于对结果做了惩罚，会使得匹配结果变小。匹配结果越大说明待识别图像与模式越一致，否则差别就比较大。
- 如图所示是8的图像。这两个数字的区别只是在最左边是否有笔画，当用8与3的模式匹配时，8的左边部分与3的模式的左边部分相乘时，会得到负值，这样匹配结果受到了惩罚，降低了匹配值。相反如果当3与8的模式匹配时，由于3的左边没有笔画值为0，与8的左边对应位置相乘得到的结果是0，也同样受到了惩罚，降低了匹配值。只有当待识别图像与模式笔画一致时，才会得到最大的匹配值。
- 数字3、8分别与3的模式的匹配值各是多少？计算结果，3与3的模式的匹配值是143，而8与3的模式的匹配值是115。可见前者远大于后者。
3. 存在的问题
- 如果想识别一个数字是3还是8，就分别和这两个数字的模式进行匹配，看与哪个模式的匹配值大，就是哪个数字。
- 如果识别0到9这10个数字，只要分别建造这10个数字的模式就可以了。对于一个待识别图像，分别与10个模式匹配，选取匹配值最大的作为识别结果就可以了。但是由于不同数字的笔画有多有少，比如1笔画就少，而8就比较多，所以识别结果的匹配值也会有大有小。
4. 使用 Sigmoid 函数
- 我们可以对匹配值用一个称作sigmoid的函数进行变换，将匹配值变换到0和1之间。sigmoid函数如下式所示，通常用σ表示。
σ
=
1
1
+
e
−
x
\sigma = \frac{1}{1 + e ^ {-x} }
σ=1+e−x1
- 从图中可以看出，当x比较大时，sigmoid输出接近于1，而x比较小时（负数），sigmoid输出接近于0。经过sigmoid函数变换后的结果可以认作是待识别图像属于该数字的概率。
5. 增加偏置项
- 但是像前面的3和8的匹配结果分别为143、115，把两个结果带入到sigmoid函数中，都接近于1了，并没有明显的区分。
- sigmoid函数并不能直接这样用，而是要“平移”一下，加上一个适当的偏置b，使得加上偏置后，两个结果分别在sigmoid函数中心线的两边，来解决这个问题：
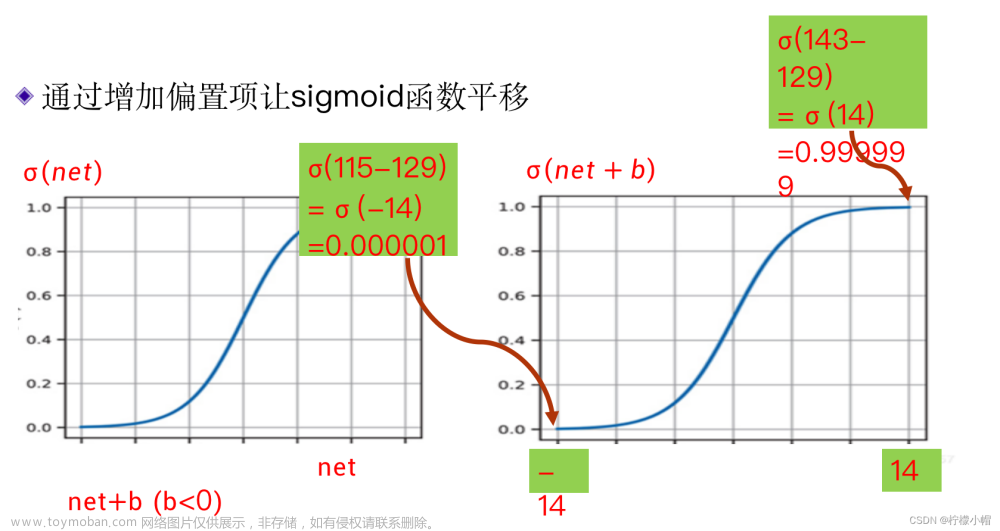
- 比如这里我们让b=-129，这样处理后的sigmoid值分别是：
- sigmoid(143-129)=0.999999
- sigmoid(115-129)=0.000001
- 这样区分的就非常清楚了，接近1的就是识别结果，而接近0的就不是。不同的数字模式具有不同的b值，这样才能解决前面提到的不同数字之间笔画有多有少的问题。
- 这是一种简单的数字识别基本原理。这与神经网络有什么关系呢？
6. 神经网络
- 上面介绍的，其实就是一个简单的神经网络。这是一个可以识别3和8的神经网络，和前面介绍的一样，
x
1
x_1
x1 …
x
n
x_n
xn 表示待识别图像，
w
3.1
w_{3.1}
w3.1 …
w
3.
n
w_{3.n}
w3.n和
w
8.1
w_{8.1}
w8.1 …
w
8.
n
w_{8.n}
w8.n 分别表示3的模式和8的模式，在图中可以看成是每条边的权重。如果用
y
3
y_3
y3 、
y
8
y_8
y8 分别表示识别为3或者8的概率的话，则这个示意图实际表示的和前面介绍的数字识别方法是完全一样的，只不过是换成了用网络的形式表达。
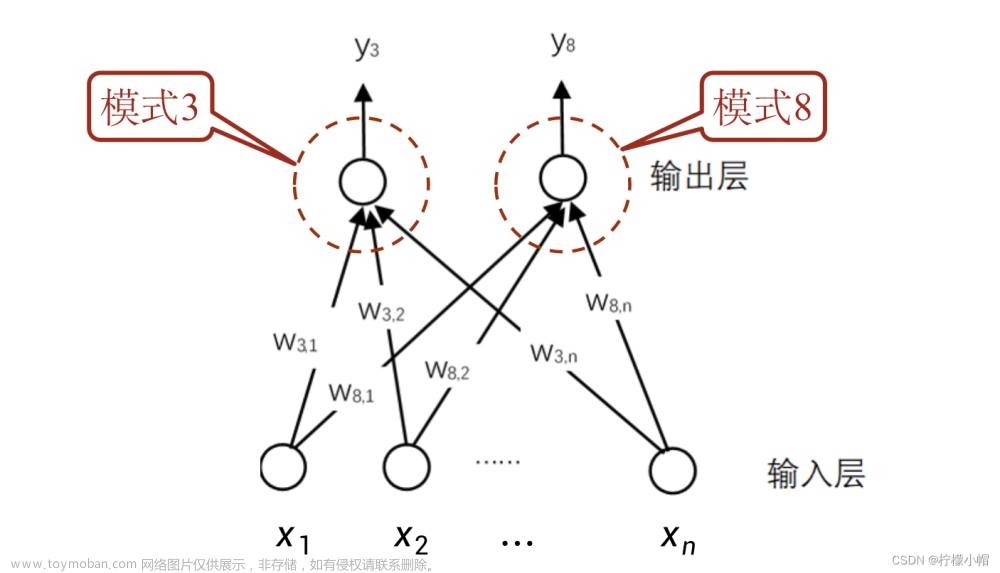
- 图中下边表示输入层，每个圆圈对应输入图像在位置
i
i
i 的值
x
i
x_i
xi ，上边一层表示输出层，每一个圆圈代表了一个神经元，所有的神经元都采取同样的运算：输入的加权和，加上偏置，再经过sigmoid函数得到输出值。这样的一个神经网络，实际表示的是如下计算过程：
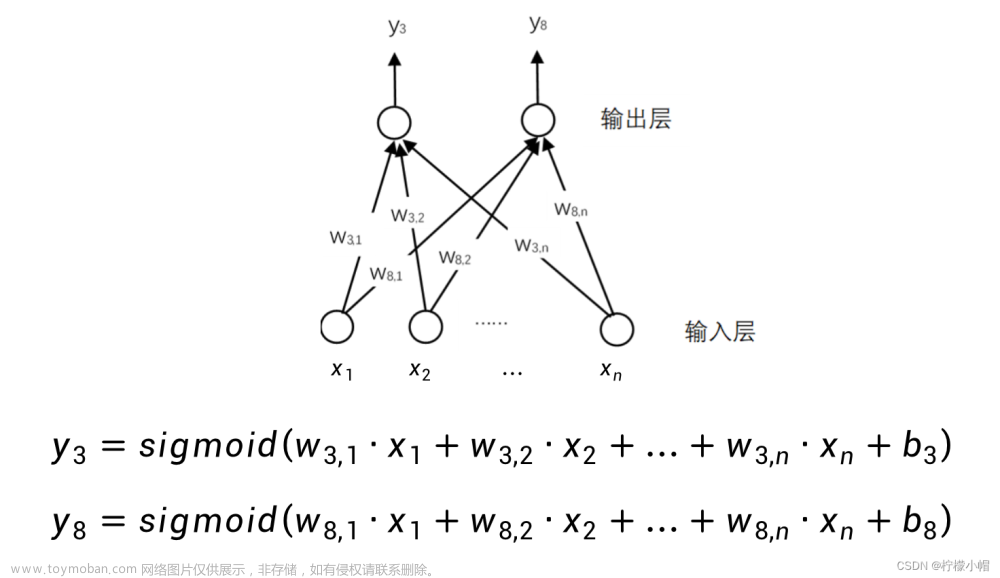
7. 数字识别神经网络
- 每个神经元对应的权重都代表了一种模式。比如在这个图中，一个神经元代表的是数字3的模式，另一个神经元代表的是数字8的模式。进一步如果在输出层补足了10个数字，就可以实现数字识别了。
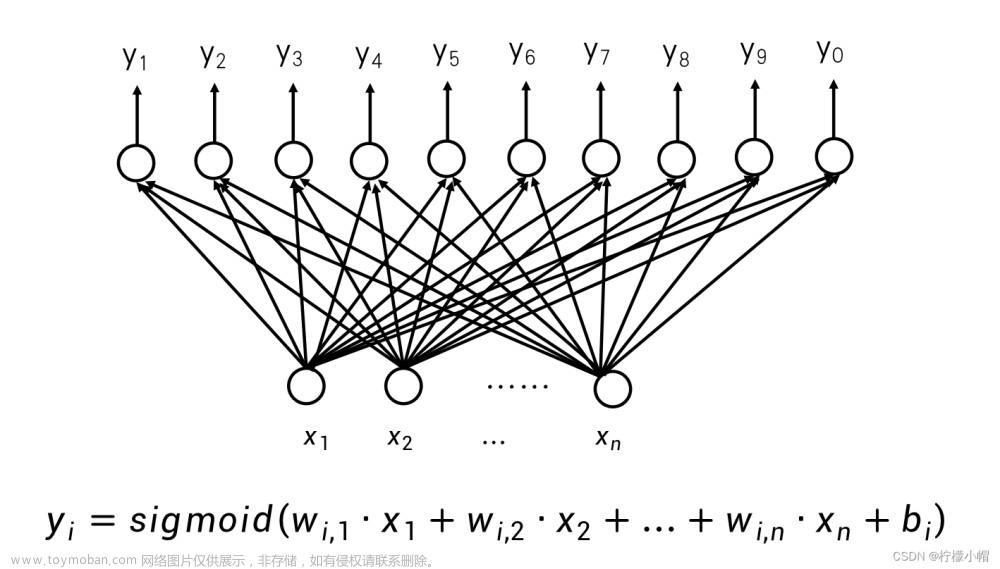
- 要识别的数字不规整，怎么办？
- 这个网络过于简单了，要想构造复杂一些的网络，可以有两个途径。比如一个数字可以有不同的写法，这样的话，同一个数字就可以构造多个不同的模式，只要匹配上一个模式，就可以认为是这个数字。这是一种横向的扩展。另外一个途径就是构造局部的模式。比如可以将一个数字划分为上下左右4个部分，每个部分是一个模式，多个模式组合在一起合成一个数字。不同的数字，也可以共享相同的局部模式。比如3和8在右上、右下部分模式可以是相同的，而区别在左上和左下的模式上。要实现这样的功能，需要在神经网络的输入层、输出层之间增加一层表示局部模式的神经元，这层神经元由于在神经网络的中间部分，所以被称为隐含层。输入层到隐含层的神经元之间都有带权重的连接，而隐含层到输出层之间也同样具有带权重的连接。隐含层的每个神经元，均表示了某种局部模式。这是一种纵向的扩展。
8. 神经网络的横向扩展 – 增加模式
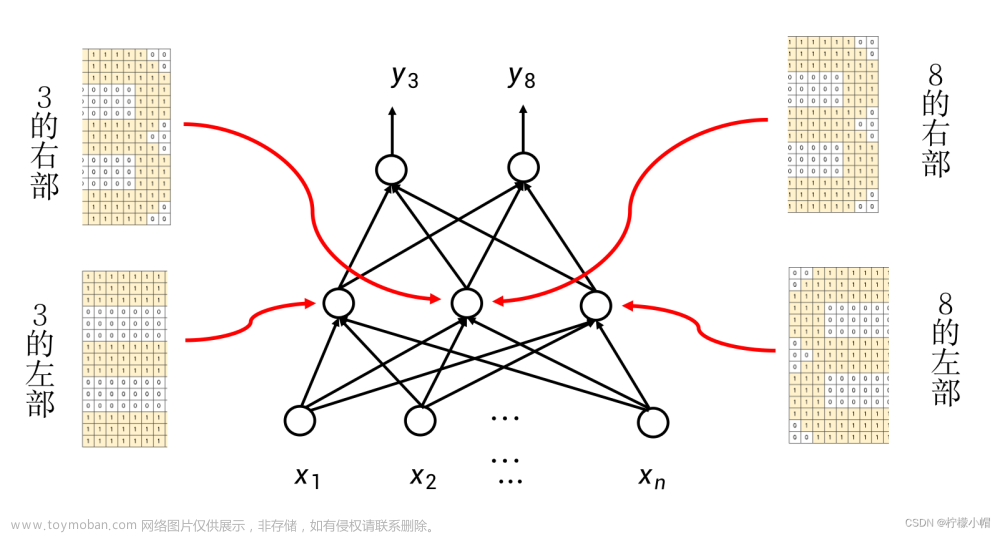
9. 神经网络的纵向扩展 – 局部模式
文章来源：https://www.toymoban.com/news/detail-709326.html
10. 让神经网络更深 - 模式组合
文章来源地址https://www.toymoban.com/news/detail-709326.html
11. 多层神经网络
- 如果要刻画更细致的局部模式，可以通过增加隐含层的数量来刻画更细致的模式，每增加一层隐含层，模式就被刻画的更详细一些。这样就建立了一个深层的神经网络，越靠近输入层的神经元，刻画的模式越细致，体现的越是细微信息的特征；越是靠近输出层的神经元，刻画的模式越是体现了整体信息的特征。这样通过不同层次的神经元体现的是不同粒度的特征。每一层隐含层也可以横向扩展，在同一层中每增加一个神经元，就增加了一种与同层神经元相同粒度特征的模式。
- 神经网络越深越能刻画不同粒度特征的模式，而横向神经元越多，则越能表示不同的模式。但是当神经网络变得复杂后，所要表达的模式会非常多，如何构造各种不同粒度的模式呢？
- 构造模式是非常难的事情，事实上我们也很难手工构造这些模式。在后面我们可以看到，这些模式，也就是神经网络的权重是可以通过样本训练得到的，也就是根据标注好的样本，神经网络会自动学习这些权值，也就是模式，从而实现数字识别。
12. 如何获得模式？
- 模式通过神经元的连接权重表示
- 通过训练样本，自动学习权重，也就是模式
- 不是人工设计！
- 学习到的模式是一种隐含表达，并不像举例的这样清晰
13. 总结
- 神经元可以表示某种模式，不同层次的神经元可以表示不同粒度的特征，从输入层开始，越往上表示的特征粒度越大，从开始的细粒度特征，到中间层次的中粒度特征，再到最上层的全局特征，利用这些特征就可以实现对数字的识别。如果网络足够复杂，神经网络不仅可以实现数字识别，还可以实现更多的智能系统，比如人脸识别、图像识别、语音识别、机器翻译等。
- 神经元实际上是模式的表达，不同的权重体现了不同的模式。权重与输入的加权和，即权重与对应的输入相乘再求和，实现的是一次输入与模式的匹配。该匹配结果可以通过sigmoid函数转换为匹配上的概率。概率值越大说明匹配度越高。
- 一个神经网络可以由多层神经元构成，每个神经元表达了一种模式，越是靠近输入层的神经元表达的越是细粒度的特征，越是靠近输出层的神经元表达的越是粗粒度特征。同一层神经元越多，说明表达的相同粒度的模式越多，而神经网络层数越多，越能刻画不同粒度的特征。
到了这里，关于人工智能AI 全栈体系（一）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
