前言
分治法首先需要明白递归的概念:
递归: 是指子程序直接调用自己或者通过一系列调用语句间接调用自己,是一种描述问题和解决问题的常用方法。递归的两个基本要素:
1.边界条件:也就是递归终止调用的条件。
2.递归出口:递归表达式,大问题分解为小问题。
分治算法的一般有几个步骤:
- 分解 :分析原来的问题,将原问题分解成一系列子问题。
- 求解:递归求解各个子问题。若子问题足够小,则直接求解。
- 合并:将子问题的解合并成原问题的解。
以下将分析几个典型例子。
1.递归解决阶乘函数
阶乘函数的定义大家都知道。
1)边界条件 n=0,n!=1
2) 递归体 n>0,n!=n*(n-1)
C语言代码:
/**
1. 阶乘的算法
2. @param n
3. @return
*/
int Fac(int n){
if(n==0)
return 1;
else
return n* Fac(n-1);
}

2.归并排序算法
2.1 归并排序的概念
归并排序是将待排序的元素分成两个大致相同的两个子序列,分别对子序列进行排序,最终将排好序的子序列合并为排序的序列。
2.2 分治法的三步曲
大致分为以下几步:
- 分解。将n个元素分成n/2个元素的子序列。
- 求解。用归并排序对两个子序列递归排序。
- 合并。合并两个排序好的子序列得到排序结果。
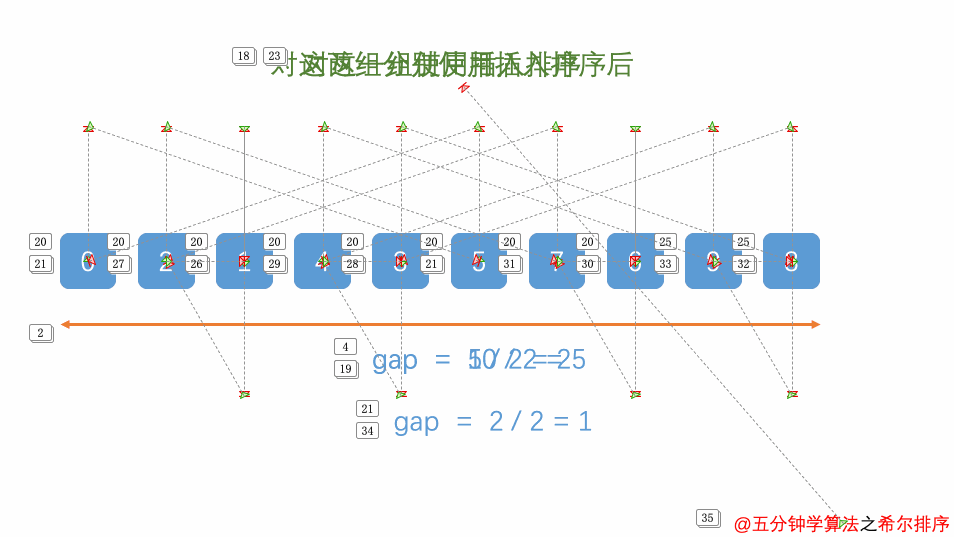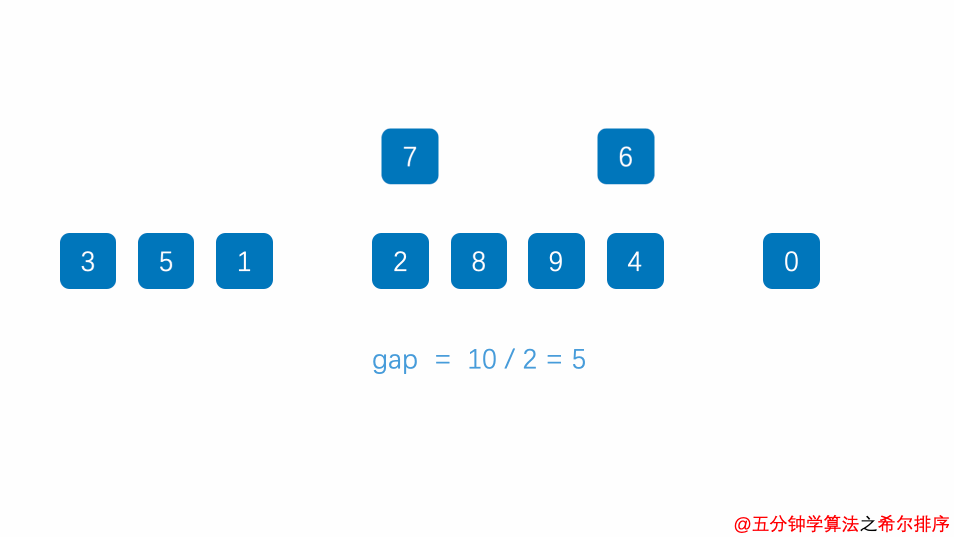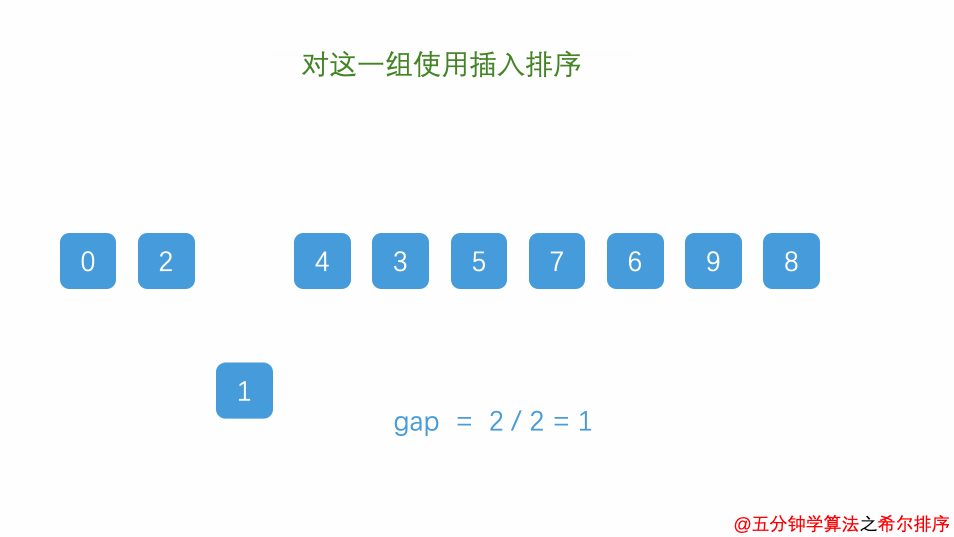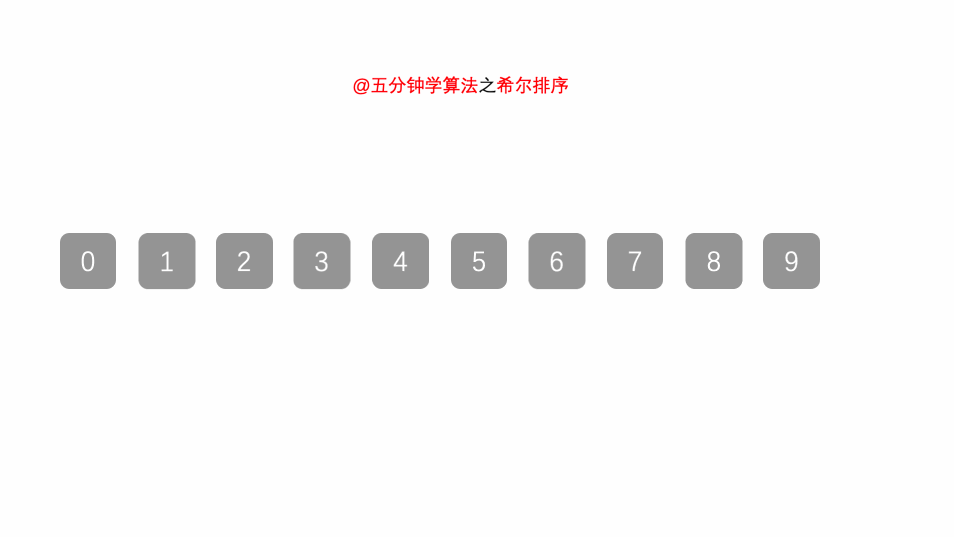
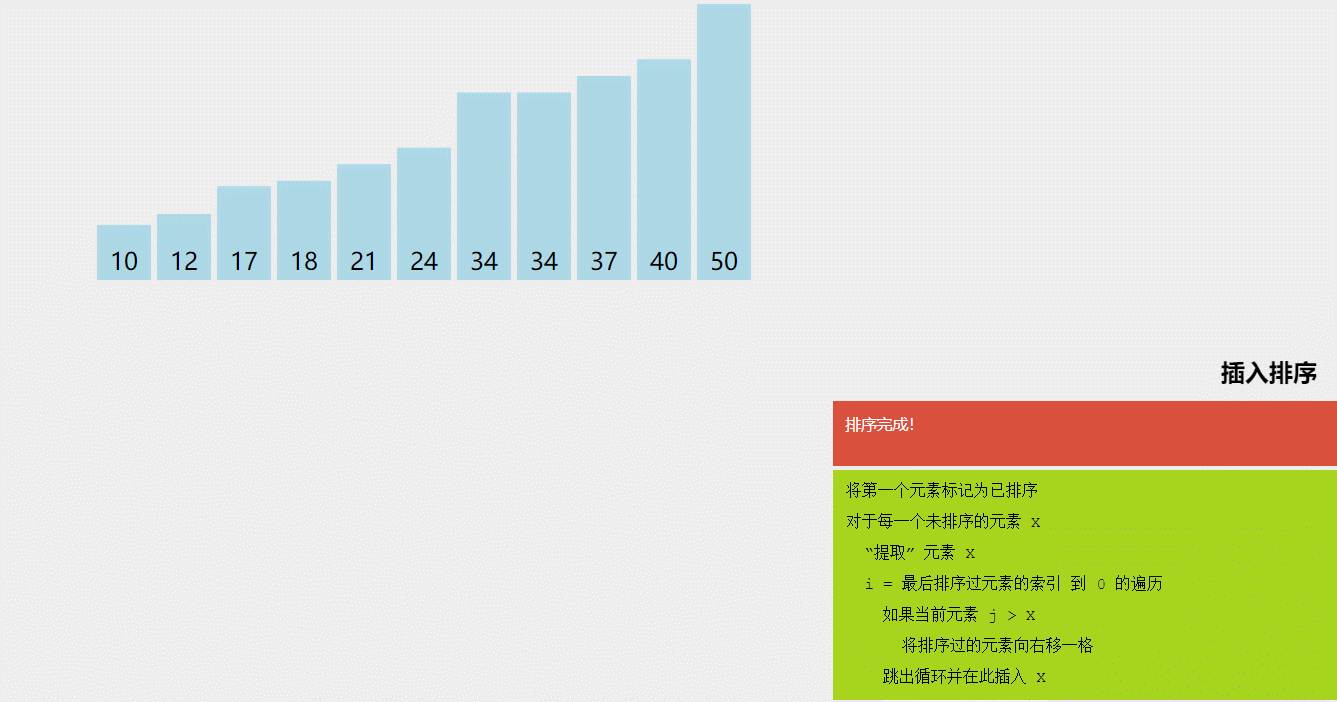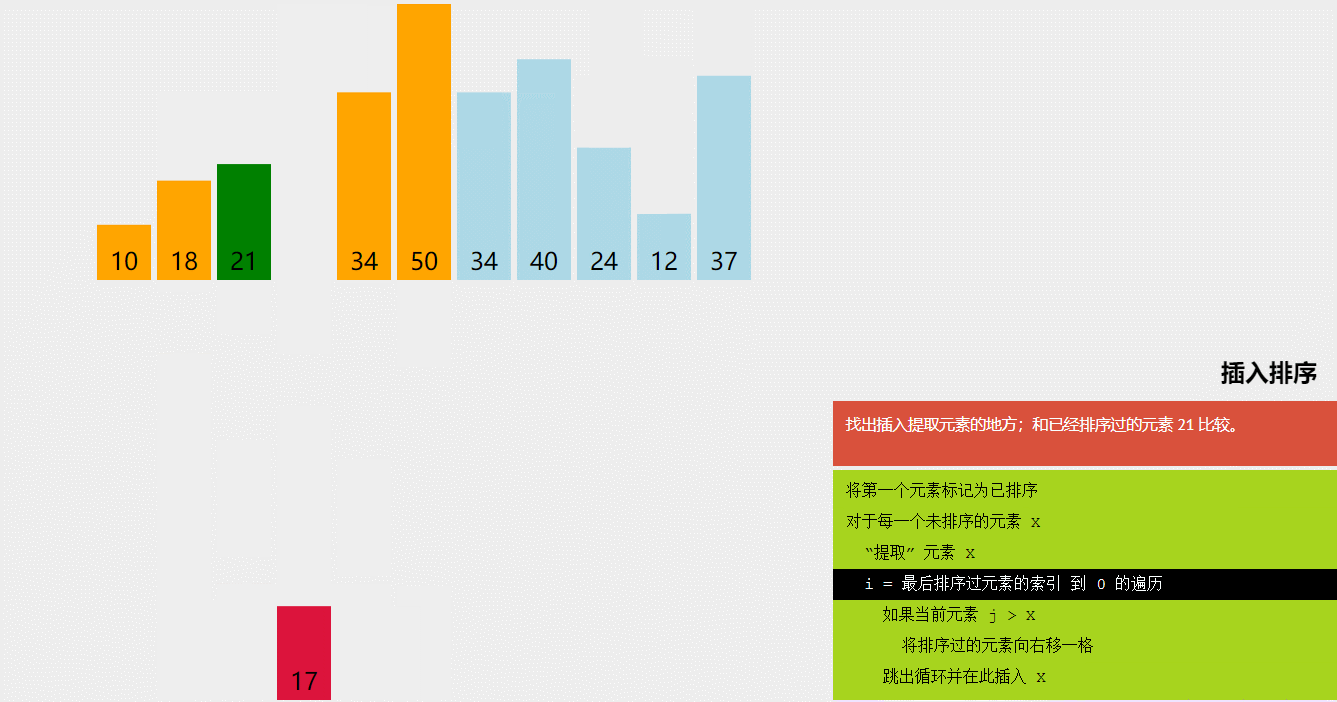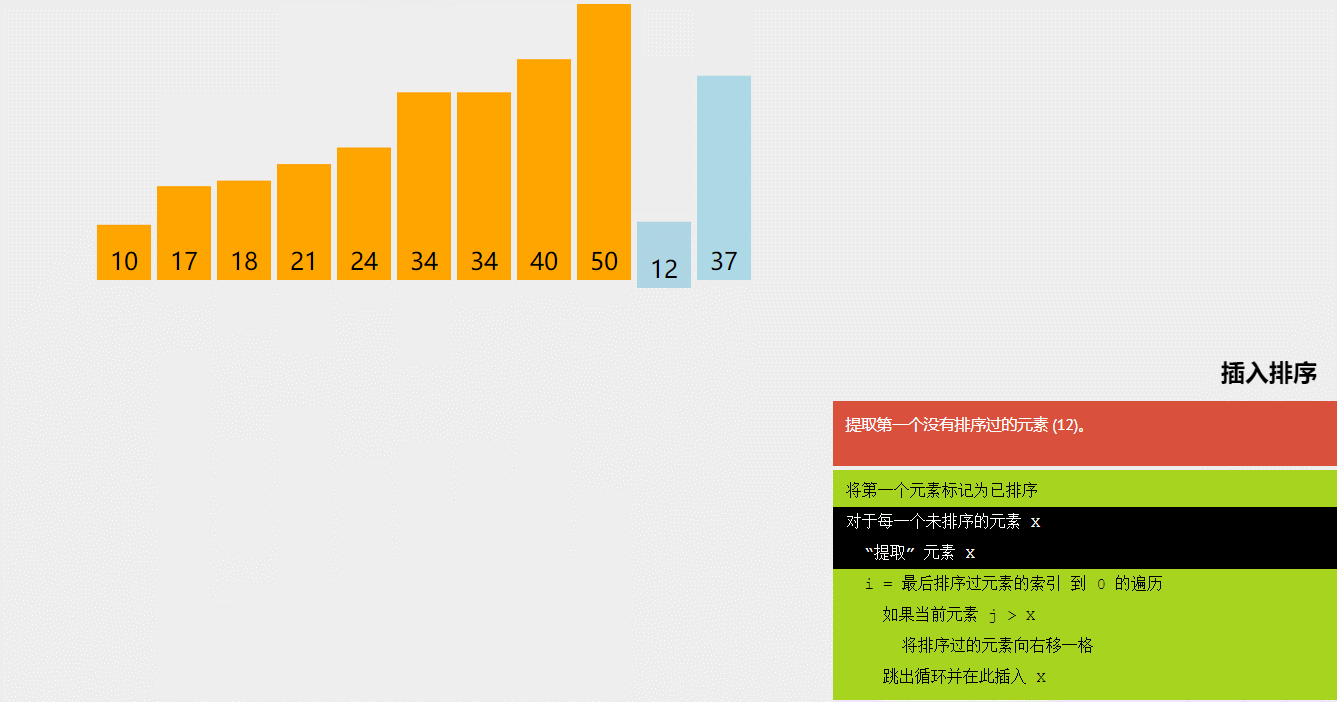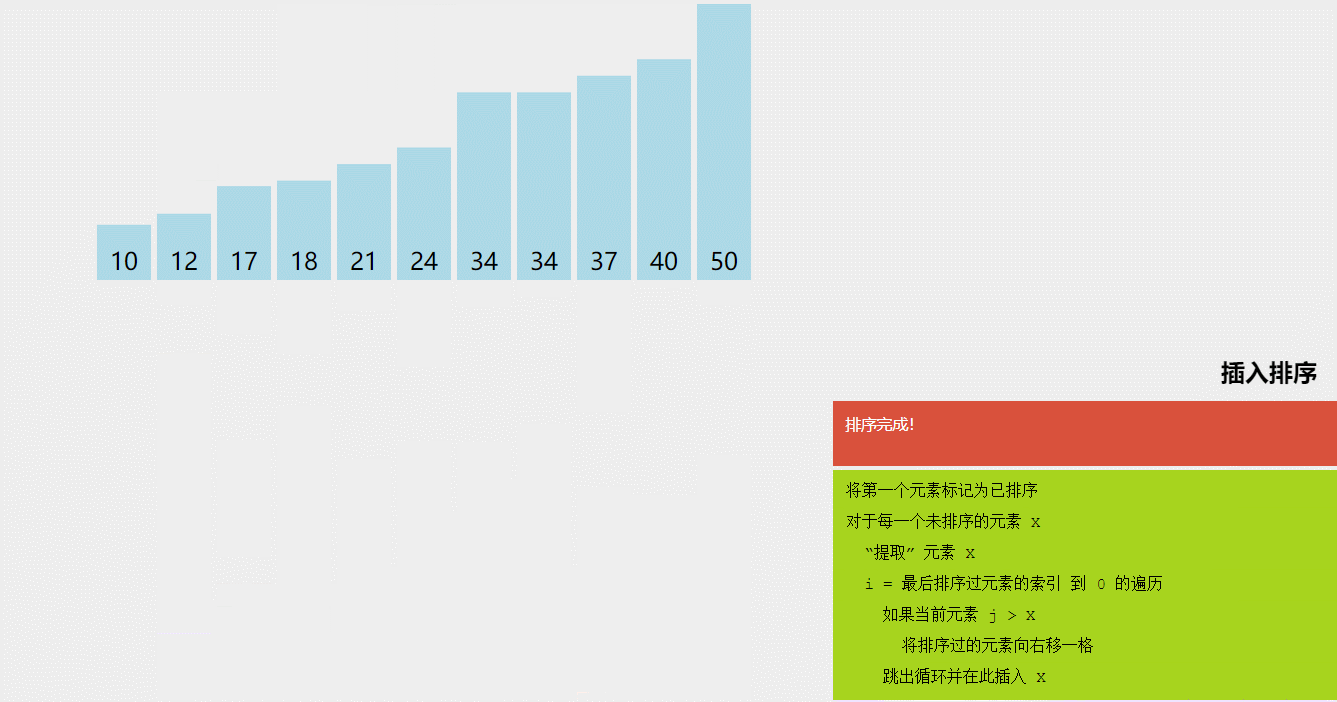
2.3 归并排序的动画

2.4 归并排序算法(C语言代码)
/**
* 归并排序
* @param a 待排序的数组
* @param l 左边的
* @param r 右端
*/
void MergeSort(int a[],int l, int r){
//计算分组的中间位置
int m;
if (l < r){
//计算中间的位置
m = (l+r)/2;
//递归左边
MergeSort(a,l,m);
//递归右边
MergeSort(a,m+1,r);
//合并结果
Merge(a,l,m,r);
}
}
/**
* 合并排序的结果
* @param a
* @param l
* @param m
* @param r
*/
void Merge(int a[], int l, int m, int r) {
//左边的长度,定义右边的长度
int lLen=m-l+1 ,rLen=r-m;
//定义临时数组存放左边的排序结果以及右边的排序结果
int L[50],R[50];
//取出左边的元素
for(int i=0 ; i < lLen ; i++){
L[i]=a[l+i];
}
//取出右边的元素
for(int j = 0 ; j < rLen; j++){
R[j]=a[m+j+1];
}
//很关键,这个值一定要设置为最大
L[lLen] = INT_MAX;
R[rLen] = INT_MAX;
//开始比较大小
int i=0,j=0;
for(int k = l; k < r+1 ; k++){
if(L[i] < R[j]){
a[k]=L[i];
i++;
}else{
a[k]=R[j];
j++;
}
}
}
测试代码:
3.最大子序列和问题
3.1 问题的定义
给定n个整型数组组成的蓄力A1,A2,…An,求该序列中子序列的字段和的最大值,当所有序列所有的整型均为负数整数时,其最大字段和为0。
example:
当序号为[-2,6,-4,8,-5,3]时,最大子序列的和为10=6+(-4)+8。
3.2 分治的思路
普通的计算,只有循环遍历所有的子段求和进行比较求解,这样的时间复杂度比较高,这种也就是暴力算法解题的思路,第一遍单个元素作为和比较,得出最大和为8,第二次遍历两个连续元素的组合,第三次遍历三个元素的组合,第四次组合…比较简单,这里不在代码。
-
分解。将序列拆分为n个子序列,最大值分为三种情况,所有序列的和分为三种情况。
(1) 所有序列的的最大字段和在序列的1/2序列左边的和相同。
(2) 所有序列的的最大字段和在序列的1/2序列右边的和相同。
(3)所有序列的的最大字段和在序列的1/2序列左和右边的和相同。 -
求解。
递归分段求解1/2字段和。由于序列是连续的,此问题的关键在于求和的时候从1/2向两边扩展求和,这样就能包含前两种情况,第三种情况是从中间1/2处左右两边子序列和的最大值。 -
合并。最终的结果就是三个情况的和最大结果。
3.3 简单的分解下代码的结果
以序列[-2,6,-4,8,-5,3]为例。
此处写比较费劲,看代码输出。文章来源:https://www.toymoban.com/news/detail-709519.html
3.4 算法代码
/**
* 打印数组
* @param a
* @param left
* @param right
*/
void printArr(int *a,int left,int right){
for (int i = left; i <= right ; ++i) {
printf("%d,",a[i]);
}
printf("\n");
}
/**
* 求解最大的字段序列和
* @param a
* @param left
* @param right
* @return
*/
int MaxSubSeqSum(int * a,int left,int right){
int sum = 0 ;
int i;
//遍历到单个元素
if(left == right){
if(a[left]>0) sum=a[left];
else sum=0;
}else{
//循环遍历
int med=(left+right)/2;
int leftSum= MaxSubSeqSum(a,left,med);
int rightSum= MaxSubSeqSum(a,med+1,right);
//计算左边的序列的字段和
int subLeftSum=0,s1=0;
printArr(a,left,med);
for ( i = med; i >=left ; i--) {
subLeftSum+=a[i];
if (subLeftSum > s1) s1=subLeftSum;
}
printf("the left sum is %d",subLeftSum);
printf("\n");
//计算右边的序列的字段和
printArr(a,med,right);
int subRightSum=0,s2=0;
for (i = med+1; i <= right ; i++) {
subRightSum+=a[i];
if (subRightSum > s2) s2=subRightSum;
}
printf("the right sum is %d",subRightSum);
printf("\n");
//左右两边之和
sum=s1+s2;
if(sum < leftSum) sum=leftSum;
if(sum < rightSum) sum=rightSum;
}
return sum;
}
3.5 测试结果
int main(){
int a[] = {-2,6,-4,8,-5,3};
int result= MaxSubSeqSum(a,0,5);
printf("the final result is :%d",result);
}
代码执行递归过程。文章来源地址https://www.toymoban.com/news/detail-709519.html
-2,
the left sum is -2
-2,6,
the right sum is 6
-2,6,
the left sum is 4
6,-4,
the right sum is -4
8,
the left sum is 8
8,-5,
the right sum is -5
8,-5,
the left sum is 3
-5,3,
the right sum is 3
-2,6,-4,
the left sum is 0
-4,8,-5,3,
the right sum is 6
the final result is :10
到了这里,关于数据结构与算法之分治法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!