图论——Kruskal重构树学习笔记-Toy模板网

这篇具有很好参考价值的文章主要介绍了图论——Kruskal重构树学习笔记。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

图论——Kruskal 重构树

最大生成树将部分内容倒置即可

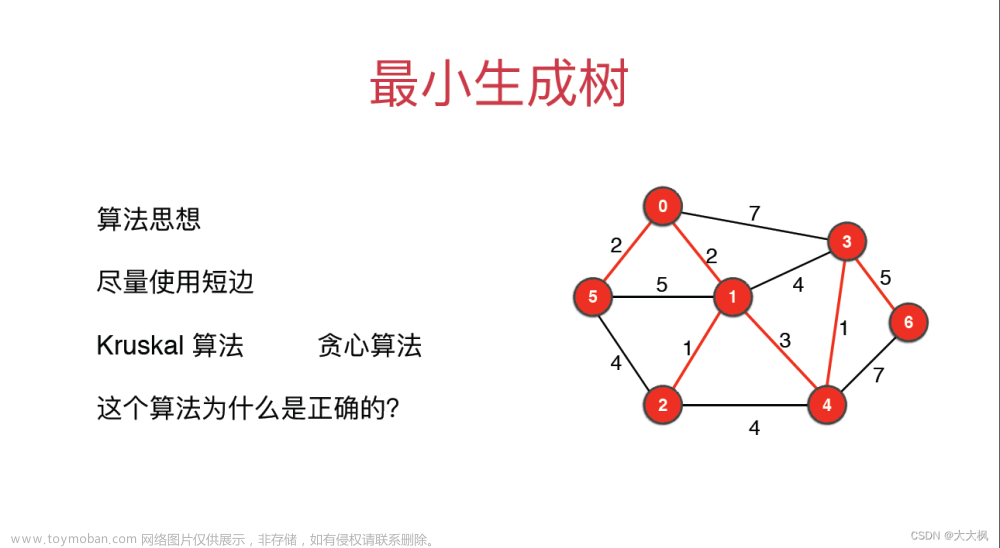
回顾：Kruskal

基本信息

求解最小生成树
时间复杂度：\(O(m \log m)\)
更适合稀疏图

算法思想

按照边权从小到大排序
依次枚举每一条边，如果这一条边两侧不连通，则加入这条边

代码

点击查看代码

const int N = 200010;

int f[N];

struct Edge
{
    int a, b, w;
    bool operator<(const Edge &W) const { return w < W.w; }
} g[N];

int find(int x) { return x == f[x] ? x : find(f[x]); }

int main()
{
    int n = rr, m = rr;

    int a, b, w;
    for (int i = 0; i < m; ++i)
        a = rr, b = rr, w = rr, g[i] = {a, b, w};

    sort(g, g + m);

    for (int i = 1; i <= n; ++i)
        f[i] = i;

    int res = 0, cnt = 0;
    for (int i = 0; i < m; ++i)
    {
        int a = find(g[i].a), b = find(g[i].b), w = g[i].w;
        if (a != b)
            f[a] = b, res += w, ++cnt;
    }

    cnt < n - 1 ? printf("impossible\n") : printf("%d\n", res);
    return 0;
}

Kruskal 重构树

算法思想

在构建最小生成树的时候，设现在枚举到了一条要加入最小生成树的边 \((u, v, w)\)：

则在 Kruskal 重构树中，构建一个点权为 \(w\) 的虚点，编号为 \(t\)，同时连边 \((u, t)\)、\((v, t)\)。

主要性质

重构树是一棵［二叉树］；
［子节点的点权］小于［父节点的点权］（即大根堆）；
最小生成树上［两点之间的最大边权］等于重构树上［两点之间的最大边权］（即为重构树上两点 LCA 的点权）。

结论证明

最小生成树上两点间最大边权等于重构树上两点 LCA 的点权，证明：

后加入的边权一定小于先加入的边权，所以重构树一定自上到下点权不减；
两点在最小生成树上的路径的所有边一定都在重构树上两点之间；
所以两点在最小生成树上之间的最长边权一定是重构树上两点 LCA 的点权。

如图：

图论——Kruskal重构树学习笔记

其中红色的点表示虚点，中间的数字表示其点权；白色的点表示原有的点。

代码

// INPUT GRAPH
const int N = 2e5 + 10;
const int M = 2e5 + 10;

// NEW GRAPH
const int NN = N + M;
const int MM = M + M;

// 4LCA
const int K = 20;

// NODE, EDGE, QUERY
int n, m, q;

// INPUT GRAPH
struct e
{
    int u, v, w;
    bool operator<(const e &t) const { return w < t.w; }
} g[M];

// UNOIN
int f[NN];
int find(int x) { return x == f[x] ? x : f[x] = find(f[x]); }

// NEW GRAPH
int d[NN], cnt;
int h[NN], e[MM], ne[MM], idx;

// 4LCA
int depth[NN];
int up[NN][K];

// ADD TO NEW GRAPH
inline void _add(int u, int v)
{
    e[idx] = v;
    ne[idx] = h[u];
    h[u] = idx++;
}

void add(int a, int b, int w)
{
    d[++cnt] = w;
    f[a] = f[b] = cnt;
    _add(a, cnt), _add(cnt, a);
    _add(b, cnt), _add(cnt, b);
}

// LCA INIT
void init(int u, int fa)
{
    depth[u] = depth[fa] + 1;
    for (int i = 1; i < K; ++i)
        up[u][i] = up[up[u][i - 1]][i - 1];

    for (int i = h[u]; i != -1; i = ne[i])
    {
        int v = e[i];
        if (v == fa)
            continue;
        up[v][0] = u, init(v, u);
    }
}

// KRUSKAL
int kruskal()
{
    sort(g + 1, g + 1 + m);

    for (int i = 1; i <= n * 2; ++i)
        f[i] = i;

    cnt = n;
    memset(h, -1, sizeof h);

    int res = 0;
    for (int i = 1; i <= m; ++i)
    {
        int u = find(g[i].u), v = find(g[i].v), &w = g[i].w;
        if (u == v)
            continue;
        res += w, add(u, v, w);
    }

    init(cnt, 0);
    return res;
}

// LCA
int lca(int x, int y)
{
    if (depth[x] < depth[y])
        swap(x, y);

    for (int i = K - 1; i >= 0; --i)
    {
        if (depth[up[x][i]] >= depth[y])
            x = up[x][i];
        if (x == y)
            return x;
    }

    for (int i = K - 1; i >= 0; --i)
        if (up[x][i] != up[y][i])
            x = up[x][i], y = up[y][i];
    return up[x][0];
}

int main()
{
    n = rr, m = rr;

    int a, b, w;
    for (int i = 1; i <= m; ++i)
        a = rr, b = rr, w = rr, g[i] = {a, b, w};

    q = rr;

    int res = kruskal();
    while (q--)
        printf("%d\n", d[lca(rr, rr)]);
    return 0;
}

Reference

[1] https://www.luogu.com.cn/blog/lizbaka/kruskal-chong-gou-shu
[2] https://blog.csdn.net/m0_61735576/article/details/124804973文章来源地址https://www.toymoban.com/news/detail-709963.html

到了这里，关于图论——Kruskal重构树学习笔记的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！