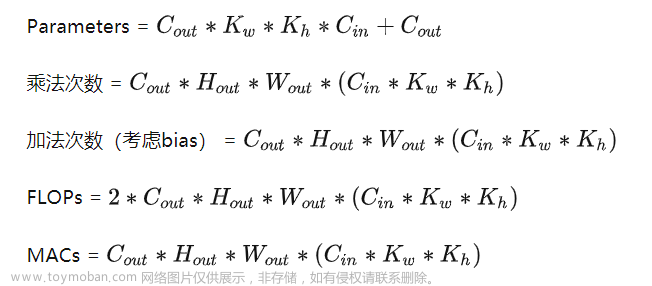前言
本篇笔记是分析transformer模型的参数量、计算量、中间激活、KV cache - 知乎 (zhihu.com)的学习记录。大部分内容都是来自那篇文字。
符号表
本文的示例模型是decoder-only模型,即若干个相同的层,有的人称之为block,每个block包含:self-attention层、MLP层(或者称为FFN层)。如下:
| 数学符号 | 定义 |
|---|---|
| \(l\) | 模型层数,即block的数量 |
| \(d\) | 隐层维度、token维度 |
| \(h\) | 注意力头数 |
| \(b\) | 训练批次大小,即batch size |
| \(s\) | 序列长度 |
| \(V\) | 词表大小 |
| \(\mu\) | 向量的均值 |
| \(\sigma\) | 向量的方差 |
模型相关计算
参数量
从输入到输出的顺序依次计算:
Embedding层:词嵌入矩阵即一个\(V\rightarrow d\)无偏置线性层,将\(V\)大小的one-hot编码映射成\(d\)大小的token。参数个数\(Vd\)。
Positional Embedding:简单起见,不考虑包含可训练参数的位置编码。
然后数据进入\(l\)个block,在每个block中首先是:
Self-attention:attention层中有四个\(d \rightarrow d\)线性层,包含了权重:\(W_q\)、\(W_k\)、\(W_v\)、\(W_{out}\)以及各自的偏置。权重矩阵n的形状\([d,d]\),参数个数\(d^2\),偏置形状\([d]\),参数个数\(d\)。总计参数量\(4d^2+4d\).
Layer Normalization:设层输入是\(x_{in}\),layer normalization公式:\(\bold{x}_{out}=\bold{\gamma}\odot \bold{a} + \bold{\beta}, \bold{a}=\frac{\bold{x}_{in}-\mu}{\sqrt{(\sigma^2)+\epsilon}}\)。其中\(\mu\)表示的均值\(x_{in}\),\(\sigma\)表示\(x_{in}\)的方差,\(\epsilon\)防止除零,\(\gamma\)和\(\beta\)是可学习的参数,形状都是\([d]\),参数个数\(d\),一层的参数个数\(2d\)。因为self-attention和mlp后各有一层layer nromalization,所以总参数个数\(4d\)。
然后是mlp层:共有两个带偏置的线性层,隐层维度默认为\(4d\):第一个是\(d\rightarrow 4d\),权重矩阵形状\([d,4d]\),偏置形状\([4d]\),层参数\(4d^2+4d\);第二个是\(4d\rightarrow d\),权重矩阵形状\([4d,d]\),偏置形状\([d]\),层参数\(4d^2+4d\)。因此mlp的总参数个数\(8d^2+5d\).
因此每个block的参数个数共计\(12d^2+13d\).
输出层和Embedding层共用参数。
因此,模型共计参数\(l*(12d^2+13d)+Vd\).
显存占用
模型参数
有多种数据类型,常见的有:
- float32(FP32):32位浮点数,也称为单精度。
- float16(FP16):16位浮点数,表示范围较小,也被称为半精度。
- bfloat16(BF16):扩大了指数位数,缩小了小数位数,因此表示的范围更大,精度更弱。
一般采用16位的表示,那么一个参数占用2byte,即2B。
模型参数共占用\(2l*(12d^2+13d)+Vd\) bytes
优化器
在训练过程中,模型的每个参数会记录梯度用于更新,此外优化器也会额外记录一些数据,称为优化器状态。
分析AdamW优化器,AdamW对模型中的每个参数记录了两个动量(一阶和二阶动量),即下面公式中的\(m_t\)和\(v_t\)。
混合精度
FP16的精度高,但是表示范围小,容易上溢;而BF16的表示范围大,但精度低,因此更容易下溢,为了避免溢出问题,提出了混合精度方案。
如上图,模型权重在前向过程中是16位,反向传播时梯度也是16位。但是在更新时,会采用32位的数据计算,也就是说,代码中复制了一份32位的模型权重,并且优化器也采用了32位的动量。
关于梯度比较有争议,如果采用了Scale up技术,那么梯度就还是16位,但是我看的博客中说复制了一份32位的梯度,按道理没必要复制一份32位,直接采用32位的就可以了。
所以对于模型每个参数,其额外的显存占用可能是:
- (4+4)+4+2 =16Bytes,分别是(两个动量)+32位参数复制+16位梯度
- (4+4)+4+4 =18Bytes,分别是(两个动量)+32位参数复制+32位梯度
- (4+4)+4+(2+4) =20Bytes,分别是(两个动量)+32位参数复制+(16位梯度+32位梯度复制)
总之,如果是第一种方案,那么对于模型中的一个可训练参数,对应的显存占用就是16B(含自身),总计\(16l*(12d^2+13d)+Vd\)Bytes.
中间激活值
反向传播
反向传播的核心是链式求导法则,形式是矩阵求导,链式求导法则很好理解,但写成矩阵求导就难了。
考虑attention第一步,将上层输入\(x\)线性变换query \(Q\):\(Q=xW_q\):
\(x\)的形状为\([b,s,d]\),\(W_q\)的形状为\([d,d]\),\(W_q\)的形状为\([b,s,d]\)。
为了简化计算便于理解,从一维到多维,这里先假设\(x\)的形状为[3](即一维向量),\(W_q\)的形状为\([3,3]\),\(Q\)的形状为\([3]\)。
那么具体的:
设损失函数为\(L\),这是一个实值函数,可以将\(L\)理解为一个标量。我们知道,梯度的定义是损失函数对某个权重的偏导,而梯度可以理解为:某个权重改变了一个单位长度后,损失函数变化的程度。也就是说,我们要求出损失函数对所有可更新参数的偏导,这样才能进行参数更新(梯度下降)。
而在这个过程中,\(W_q\)是要更新的权重矩阵,\(x\)是下层输入(随样本数据的变化而变化)。对\(W_q\)中一个参数的具体的求导过程如下:
可以更抽象的解释一下上面的结果:\(w_{12}\)表示第1个位置的输入\(x_1\)对第2个位置的输出\(q_2\)的贡献权重。因此先计算\(q_2\)对\(L\)的影响,再计算\(w_{12}\)对\(q_2\)的影响(根据公式的形式是后计算\(w_{12}\)对\(q_2\)的影响,实际上在前向过程中先计算),根据链式求导法则,二者相乘得到\(w_{12}\)对\(L\)的影响。
相似的,对\(W_q\)中各权重的求导结果如下:
为了便于书写,现在引入一种新的形式——对矩阵求导:
就是按元素位置对应求导,向量也是一样(数学形式上,向量就是行为1的二维矩阵)。
那么对\(W_q\)中各权重的求导结果就可简单的表示为:
注意,这里的\(x\)是一个一维向量,形状\([3]\),在attention中,每个序列的输入\(x\)的形状是\([s,d]\),这里假设为\([2,3]\),提升了一个维度上式同样成立。简单说一下就是\(w_{12}\)表示:\(x_{11}\)与\(q_{12}\)、\(x_{21}\)与\(q_{22}\)之间的权重,于是:
总之,根据计算结果,当我们反向传播更新权重\(W_q\)时,需要两个参数\(x^T\)和\(\frac{\partial{L}}{\partial \bold{Q}}\),其中\(\frac{\partial{L}}{\partial \bold{Q}}\)只能反向传播过程才能得到。而\(x^T\)在前向过程中,也\(Q=xW_q\)就是过程中,就可以计算得到了,于是\(x^T\)(程序中直接保存\(x\)和)就是\(xW_q\)和的中间激活值。
中间激活值显存计算
中间激活值也采用16位浮点数,占2bytes
首先应该是Embedding层的中间激活值,但是文章中说不需要,考虑到Embedding层和输出层参数贡献,我猜测是两种可能之一:
- 仅在Embedding层更新参数,输出层参数固定。假设\(\bold{x}=\bold{Seqs}\bold{W}_E\),中间激活就是\(Seqs\),而\(Seqs\)可能已经保存在显存中了,不作为中间激活额外保存。
- 仅在输出层更新参数,Embedding层参数不更新。假设\(logits=xW_E\),那么中间激活就是\(x\)。
这里假设是第二种。
然后考虑Multi-mask Self-attention:
-
对于\(x\bold{W}_q,x\bold{W}_k,x\bold{W}_v\),第一层block中输入attention层的\(x_0\)可能没有参与过可训练参数的计算,所以不用计算\(\frac{\partial{L}}{\partial \bold{x_0}}\),但是后续block中既要算\(\frac{\partial{L}}{\partial \bold{x_i}}\)也要算\(\frac{\partial{L}}{\partial \bold{W}_q^i}\),需要保存\(W_q\)和\(x\),但是\(W_q\)本身就是模型参数,不需要额外保存,因此不是中间激活。所以中间激活只有\(x\),形状为\([b,s,d]\),占用显存大小\(2bsd\)bytes。
-
对于\(c\),需要计算\(\frac{\partial{L}}{\partial \bold{Q}}\)和\(\frac{\partial{L}}{\partial \bold{K^T}}\),各自需要保存Q和\(K^T\),\(Q,K\)的形状都是\([b,h,s/h,d]\),共计占用显存大小\(4bsd\)bytes。
-
对于\(Softmax(\frac{QK^T}{\sqrt{d}})\),设\(S=Softmax(\bold{t})\),其中\(\bold{t}=[t_1,...,t_n],S=[s_1,...,s_n]\)。则:
\[\frac{\partial s_i}{\partial t_j}=\frac{\partial}{\partial t_j}(\frac{e^{t_i}}{\sum_k{e^{t_k}}})= \begin{cases} -s_i s_j& \text{i != j} \\ s_i(1-s_i)& \text{i == j} \end{cases} \\ \frac{\partial S}{\partial t}=[\frac{\partial s_i}{\partial t_j}]_{i=0,j=0}^{nn}=diag(S)-S^TS \]按道理,需要保存的是\(S=Softmax(\bold{t})\)的结果,但是我看文章中写的是保存\(QK^T\),不管是哪个,形状都是\([b,h,s/h,d,d]\),占用显存大小\(2bsd\)bytes。
-
对于\(S(score)·V\),保存\(S(score)\)和\(V\),形状分别是\([b,h,s/h,d,d]\)和\([b,h,s/h,d]\),共占用显存\(2bsd^2+2bsd\)bytes。
-
对于\(V_{out}·W_o,V_{out}=S(score)·V\),保存\(V_{out}\)和\(W_o\),但是\(W_o\)是模型参数不用额外保存,\(V_{out}\)形状为\([b,h,s/h,d]\),共占用显存\(2bsd\)bytes。
-
dropout,不太清楚,元素用1byte存储,占用显存\(bsd\)bytes。
-
Self-attention层总计显存占用\(11bsd+5bsd^2\)。
Layer Normalization:
不会算,根据资料,需要保存输入\(x\),以及方差\(\sigma\)和均值\(\mu\),共计\(2bsd+2bs\)bytes。一共有两层LN,并且省略方差和均值的显存占用,共计\(4bsd\)bytes。
MLP层:
- 线性层\(d\rightarrow 4d\),保存输入,占用显存\(2bsd\)bytes。
- 激活层,不会算,保存输入,占用显存\(8bsd\)bytes。
- 线性层,保存输入,占用显存\(8bsd\)bytes。
- dropout,保留mask矩阵,占用显存\(bsd\)bytes。
- 总计\(19bsd\)bytes。
中间激活值占用显存总计\((34bsd+5bsd^2)\)bytes。
最终\(l\)层block中间激活层共计\(l*(34bsd+5bsd^2)\)bytes
于是总的显存占用为\(16l*(12d^2+13d)+Vd+l*(34bsd+5bsd^2) + bsd\)bytes.
计算量
一次矩阵运算,例如\(QK^T\),一共有\(b*s^2\)个元素,每个元素的计算都进行了\(d\)次的加法和\(d\)次的乘法,浮点数的一次加法或者乘法运算就被称为一次浮点数运算,总共做了\(2bs^2d\)次浮点数运算。
| 阶段 | 运算 | 浮点数运算 |
|---|---|---|
| Embedding | \(x=SeqsW_E\) | 因为one-hot非常稀疏,浮点运算次数未知 |
| Self-attention | \(x\bold{W}_q,x\bold{W}_k,x\bold{W}_v\) | \(3*bsd*2d=6bsd^2\) |
| Self-attention | \(QK^T\) | \(bs^2*2d=2bs^2d\) |
| Self-attention | \(Softmax(\frac{QK^T}{\sqrt{d}})\) | \(bs*4s=4bs^2\) |
| Self-attention | \(S(score)·V\) | \(bsd*2s=2bs^2d\) |
| Self-attention | \(V_{out}·W_o\) | \(bsd*2d=2bsd^2\) |
| Layer Normalization | \(a=\frac{x_{in}-\mu}{\sqrt{(\sigma)^2+\epsilon}}\) | \(bs*3d=3bsd?\) |
| Layer Normalization | \(\bold{\gamma}\odot \bold{a} + \bold{\beta}\) | \(bs*2d=2bsd\) |
| MLP | \(xW_1\) | \(4bsd*2d=8bsd^2\) |
| MLP | \(GeLu(xW_1)\) | 未知 |
| MLP | \(xW_2\) | \(bsd*8d=8bsd^2\) |
| 输出层 | \(logits=xW_E^T\) | \(bsV*2d=2bsdV\) |
| 总计 | 忽略复杂度较低的 | \(l*(24bsd^2+4bs^2d)+2bsdV\) |
训练时间
根据浮点计算次数以及显卡计算速度和利用率计算训练时间。
显卡利用率一般在0.35到0.5之间。
KV Cache
kv cache是推理时采用的技术,是一种空间换时间的方案。
没有kv cache的推理过程中有大量的重复计算,例如重复计算\(x\bold{W}_q,x\bold{W}_k,x\bold{W}_v\)。
因为推理是自回归的,很自然的会把代码写成下面的形式:
import torch
from transformers import GPT2LMHeadModel, GPT2Tokenizer
model = GPT2LMHeadModel.from_pretrained("/WORK/Test/gpt", torchscript=True).eval()
# tokenizer
tokenizer = GPT2Tokenizer.from_pretrained("/WORK/Test/gpt")
in_text = "Lionel Messi is a" # 很多文章也叫做prompt
in_tokens = torch.tensor(tokenizer.encode(in_text))
# inference
token_eos = torch.tensor([198]) # 句段结束标志。
out_token = None
i = 0
with torch.no_grad():
while out_token != token_eos:
logits, _ = model(in_tokens)
out_token = torch.argmax(logits[-1, :], dim=0, keepdim=True) # 取序列末尾的token对应的输出用来预测下一个词
in_tokens = torch.cat((in_tokens, out_token), 0)
text = tokenizer.decode(in_tokens) # 将tokens变成句子
print(f'step {i} input: {text}', flush=True) # 输出句子
i += 1
out_text = tokenizer.decode(in_tokens)
print(f' Input: {in_text}')
print(f'Output: {out_text}')
对于代码中的in_text,也就是prompt来说,每一次循环,都要计算\(x\bold{W}_q,x\bold{W}_k,x\bold{W}_v\),利用矩阵乘法的分块乘性质,将这些结果保存,只需要计算新的token的\(x_i\bold{W}_q,x_i\bold{W}_k,x_i\bold{W}_v\),就可以大大减少计算量。
参考资料:
分析transformer模型的参数量、计算量、中间激活、KV cache - 知乎 (zhihu.com)
[LLM]KV cache详解 图示,显存,计算量分析,代码 - 知乎 (zhihu.com)
反向传播算法推导过程(非常详细) - 知乎 (zhihu.com)文章来源:https://www.toymoban.com/news/detail-710184.html
大模型推理性能优化之KV Cache解读 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/630832593)文章来源地址https://www.toymoban.com/news/detail-710184.html
到了这里,关于模型参数以及内存的计算方法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!