矩阵的乘法运算与css的3d变换（transform）-Toy模板网

这篇具有很好参考价值的文章主要介绍了矩阵的乘法运算与css的3d变换（transform）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

theme: qklhk-chocolate

引言：你有没好奇过，在一个使用了transform变换的元素上使用window.getComputedStyle(htmlElement)['transform'] 查询出来的值代表什么？

为什么硬件加速要使用transform，以及为什么硬件加速会快?

小科普：关于矩阵的乘法

	以两个二阶齐次矩阵相乘为例
	[                 [                      [
	 a11,a12,     *     b11,b12,       =      a11*b11 + a12* b21 , a11*b12 + a12*b22,
	 a21,a22            b21,b22               a21*b11 + a22* b21 , a21*b12 + a22*b22
	]                  ]                      ]

由此，可以看到两个矩阵相乘就是拿第一个的每一行，乘以第二个的每一列，因此两个矩阵相乘也有个规定就是第一个矩阵的列数(每一行元素的个数),要与第二个矩阵的行数(每一列元素的个数)相等才可以发生乘法运算。

首先回答第一个问题：由window.getComputedStyle(htmlElement)['transform']查询出来的值代表一个matrix3d函数的参数，形如matrix3d(a1, b1, c1, d1, a2, b2, c2, d2, a3, b3, c3, d3, a4, b4, c4, d4)

其中a1 b1 c1 d1 a2 b2 c2 d2 a3 b3 c3 d3，代表了线性变换，a4 b4 c4 d4代表的是位移变换。若空间中点的表示是一个列向量表示，那么，他的矩阵形式应该是这样的:

  a1 a2 a3 a4
  b1 b2 b3 b4
  c1 c2 c3 c4
  d1 d2 d3 d4

在下边的例子中我们都假定空间中的点是以列向量形式表示的。使用右手坐标系。

（实际这里也可以写成该矩阵的转置形式，在下边进行乘法运算时都分别转置下，然后交换两个矩阵的位置也是可以的，结果是一样的）

3d变换的初始矩阵如下:

这是一个单位矩阵，这样的矩阵满足矩阵乘法运算的交换律，且和整数中1的作用一样，乘以任何数还是任何数，因此单位矩阵与其他矩阵的乘法运算不产生任何效果。

translate

translate代表一个位移变换，3d的translate变换矩阵对应的是一个如下的4阶齐次矩阵 T :

假设空间内某个点D的坐标形如:

 x
 y
 z
 1

给他施加一个translate矩阵之后就可以得到的结果为 T*D :

 1*x + 0*y + 0 * z + dx,               x + dx
 0*x + 1*y + 0 * z + dy,         =     y + dy
 0*x + 0*y + 1 * z + dz,               z + dz
 0 +   0   +  0    + 1,                   1

以上的变换写成matrix3d函数的形式就是:
matrix3d(1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, dx, dy, dz, 1)
等价于:
translate3d(x,y,z)。

变换矩阵的前三行可以分别看做一个空间坐标系上对某个点要施以某种变换的x，y，z轴上的表示，每一行的前三列代表x,y,z轴上具体要有的变换，比如在位移变换矩阵中第一行代表x轴上该点要做的变换，那么对应的y,z的值为0。（这是我个人的一点思考。可跳过。。。）

scale

scale表示的是一个缩放变换，缩放的具体数值体现在主对角线上，比如一个1.5倍的缩放矩阵S:

1.5   0   0   0
 0   1.5  0   0
 0    0  1.5  0
 0    0   0   1

给上边的点D施加一个缩放矩阵得到的结果是 S*D:

	1.5*x + 0*y   + 0*z  + 0 * 1      1.5x
    0*x  + 1.5*y + 0*z  + 0 * 1   =  1.5y
    0*x +  0*y +  1.5*z + 0 * 1      1.5z
    0*x +  0*y +   0*z  + 1 * 1       1

等价于:
matrix3d(1.5, 0, 0, 0, 0, 1.5, 0, 0, 0, 0, 1.5, 0, 0, 0, 0, 1)
可简写为:
scale3d(1.5, 1.5, 1.5)

rotate

rotate 代表旋转

二维平面的rotate

二维平面的rotate代表某个点绕着某个点旋转，一个二维变换可以使用一个三阶齐次矩阵表示，其矩阵的推导可以这么推导:

首先是主对角线上的缩放数值，和第三列的位移值，都为默认值1（代表原始大小）和0（代表原始位置）:

1 0 0
0 1 0
0 0 1

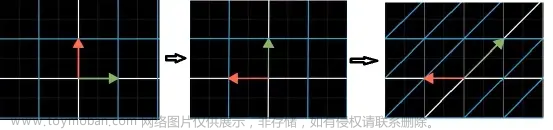
我们拿如下二维坐标系举例:

将两个单位向量分别在x y轴上旋转θ角度，得到的A'便是x轴上旋转矩阵的值，得到的B' 便是y轴上旋转矩阵的值，因此2d的旋转矩阵是这样的(图片上的坐标系是以行向量表示的，为了统一我们进行一次转置):

cos0   -sin0
sin0   cos0

3d空间的rotate

在一个3d空间中，旋转不再是绕某个点的旋转，而是绕某个轴的旋转(x,y,z轴)，以绕x轴的旋转举例(这个图有点出入，实际BB'应该与y轴是平行的，AA'与Z轴平行，理解就好，没办法绘画功底实在太差 - -，绕某个轴旋转就是想象该条轴不动然后另一条与他垂直的轴绕着其旋转)：
矩阵的乘法运算与css的3d变换（transform）

因此绕x轴的旋转矩阵可以写成这样：

1    0    0     0
0  cos0  -sin0  0
0  sin0   cos0  0
0    0     0    1

我们可以写一个rotateX(60deg),那么对应的matrix3d的参数就是:
matrix3d(1, 0, 0, 0, 0, 0.5, 0.866025, 0, 0, -0.866025, 0.5, 0, 0, 0, 0, 1)
同理可得出绕z轴和y轴的旋转矩阵:

Z:
cos0 -sin0 0 0
sin0 cos0  0 0
 0    0    1 0
 0    0    0 1
 
 Y：
 cos0   0   sin0   0
  0     1     0    0
 -sin0  0   cos0   0
  0     0     0    1

至此，css中的3d变换大体上讲完了，然后将以上几种矩阵经过不同组合相乘就能得到复合变换，值得注意的是矩阵乘法一般不满足交换律，所以运算顺序还是比较重要的。

那为什么图形变换在计算机中一般使用矩阵表示呢？据我现在看到的资料来看，就是方便，使用矩阵运算之后，可以将多种变换统一成矩阵的乘法运算，方便计算机流水线式处理。
最后回答一下第二个问题：

2.为什么硬件加速要使用transform，以及为什么硬件加速会快?
第一点是因为css的3d transform属性使用在一个元素上该元素会被提升成一个单独的layer，在一个单独的layer上使用一些变换可以直接跳过浏览器渲染的一般流程layout，paint，直接在计算结束之后进行一次composite ，这是快的第一点，第二点是因为使用transform变换的元素其运算发生在gpu上，而gpu的多核在处理并发运算的时候本身就要比cpu快基本是这样。

最后分享一个矩阵的乘法运算，可以验证一下css transform相关的矩阵运算

 // 矩阵相乘
 function multipy(a,b){
        let r = a.length;
        let col = a[0].length;
        let result = [];
        for( let i = 0; i < r; i++ ){

            let row = a[i];
            result[i] = [];

            for( let j = 0; j < r; j++){
                let count = 0;
                for( let x = 0;x < col; x++ ){
                    let item1 = row[x];
                    let item2 = b[x][j]
                    count += (item1*item2)
                }
                result[i].push(count)


            }
        }
        return result;

    }
    const deg45 = Math.PI/4;