动态规划——状压DP 学习笔记
引入
前置知识:位运算
动态规划的过程是随着阶段的增长,在每个状态维度上不断扩展的。
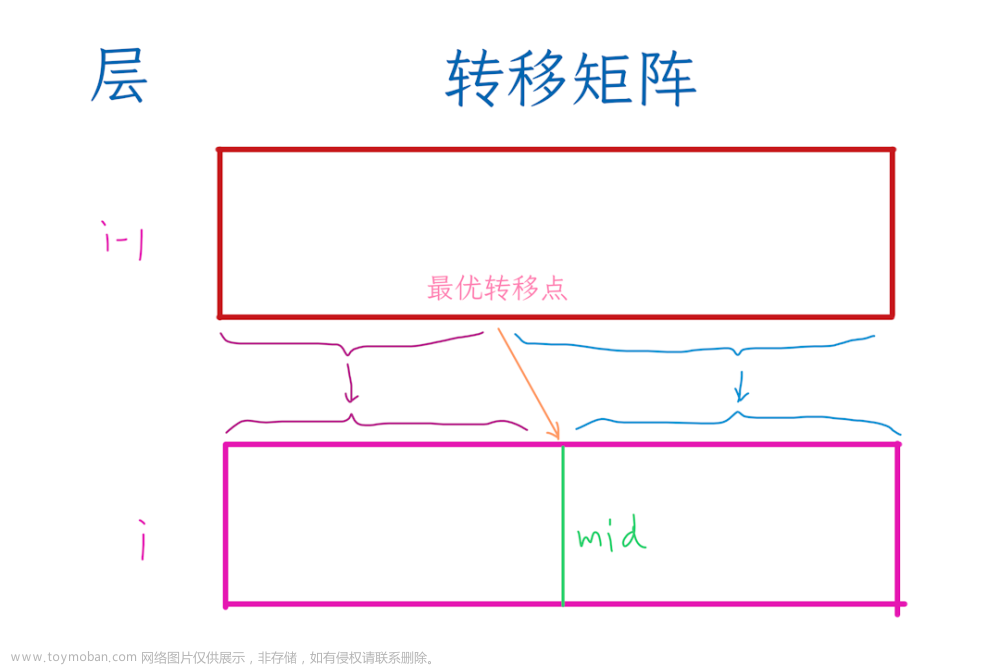
在任意时刻,已经求出最优解的状态与尚未求出最优解的状态在各维度上的分界点组成了 DP 扩展的“轮廓”。对于某些问题,我们需要在动态规划的“状态”中记录一个集合,保存这个“轮廓”的详细信息,以便进行状态转移。
若集合大小不超过 \(N\),集合中每个元素都是小于 \(K\) 的自然数,则我们可以把这个集合看作一个 \(N\) 位 \(K\) 进制数,以一个 \([0, K^{N - 1}]\) 之间的十进制整数的形式作为 DP 状态的一维。这种把集合转化为整数记录在 DO 状态中的一类算法,就被称为状态压缩的动态规划算法。
定义
意义
状态压缩,即在数据范围较小的情况下,将每个物品或者东西选与不选的状态压缩为一个整数的方法。
状态压缩,即以最小代价来表示某种状态的方式,通常是用一串二进制数(\(01\) 串)来表示各个元素的状态,通常我们称这些情况叫做子集、设为 \(S\)。
然而还有其他的状压方法,例如三进制状压法等等,但不大常用。
本质
所以状压 DP,本质上是与 DP 无异的,它没有改变 DP 本质的优化方法,阶段还是要照分,状态还是老样子,决策依旧要做,转移方程还是得列,最优还是最优,无后性还是无后性,所以它还是比较好理解的。所以最明显的标志就是数据不能太大,大约是 \(n \le 20\)。
遍历所有状态的正确姿势就是用二进制的位运算来遍历。这大概就是状压 DP 的精髓了吧!
应用
什么时候用?
- 数据范围:范围在 \(20\) 左右时正常的状压;很多时候会有一些 NP 问题会用状压求解。
- 是否可以压缩:一般的状态压缩都是选择或者不选择,放或者不放,遇见这种东西一般时状压。
- 常见题目模型:比如 TSP,覆盖问题之类的。经常会有这种模型的题出现就可以使用状压。
状态设计
在使用状压 DP 的题目当中,往往能一眼看到一些小数据范围的量,切人点明确。而有些题,这样的量并不明显,需要更深人地分析题目性质才能找到。
- 状态跟某一个信息集合内的每一条都有关。
- 若干条精简而相互独立的信息压在一起处理。(如每个数字是否出现)
例题:旅行商(TSP)问题
状态压缩最经典的问题应该就是旅行商问题了。
问题描述
旅行商问题(Travelling Salesman Problem,TSP),给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短回路。
如何运用状态压缩
比如一共有 \(5\) 个点:\(\{1\:2\:3\:4\:5\}\)。现在要表示已经走过的地方和没走过的地方,我们可以用 \(\{0, 1\}\) 来表示。其中 \(0\) 表示没到过,\(1\) 表示到达过。那么对应的状态有:
1 2 3 4 5
0 0 0 0 0(刚要开始走,还没有到达的地方)
0 0 0 0 1(已经到过第五个点)
0 0 0 1 0(已经到过第四个点)
0 0 0 1 1(已经到过第四,五个点)
......
我们发现以上的状态可以用二进制数表示,二进制数就是由 \(\{0, 1\}\) 组成的。并且 \(2^5\) 可以涵盖所有的情况,从 \(0\:0\:0\:0\:0\) 到 \(1\:1\:1\:1\:1\);
\(dp[i][S]\) 表示走到 \(i\) 这个点,已经经过的地方为 \(S\),此时所走过的最短路。
状态转移
举个栗子,当 \(S = (11011)_{\mathrm B}\) 的时候,\(S\) 可以是由 \(11001\) 来,也可以是从 \(11010\) 来:
for (int j = 1; j <= n; ++j) {
if (i == j || (s & (1 << (j - 1))) == 0) continue;
dp[i][s] = min(dp[i][s], dp[j][s - (1 << (i - 1))] + dis(i, j));
}
练习题
见:https://www.luogu.com.cn/training/384914文章来源:https://www.toymoban.com/news/detail-710481.html
Reference
[1] https://www.luogu.com.cn/blog/new2zy/zhuang-ya-zhuang-ya-post
[2] https://www.luogu.com.cn/blog/yijan/zhuang-ya-dp
[3] https://www.luogu.com.cn/blog/DestinHistoire/zhuang-tai-ya-su-dp
[4] https://www.cnblogs.com/maoyiting/p/13368682.html
[5] https://blog.csdn.net/qq_44579321/article/details/129489274
[6] https://blog.csdn.net/weixin_44254608/article/details/105761281文章来源地址https://www.toymoban.com/news/detail-710481.html
到了这里,关于动态规划——状压DP 学习笔记的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!