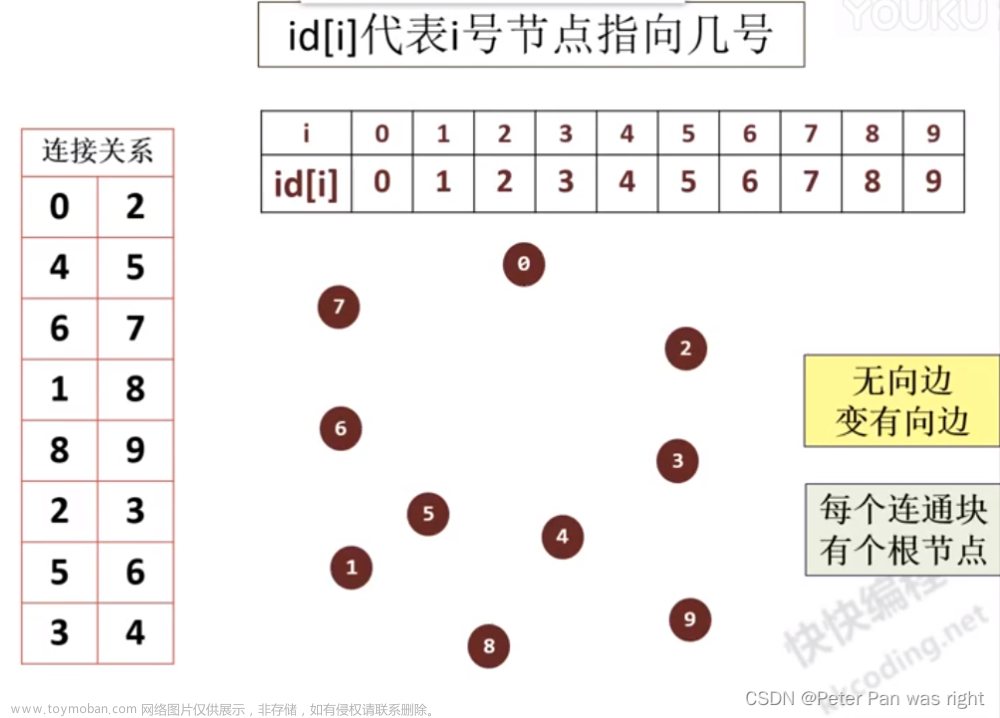
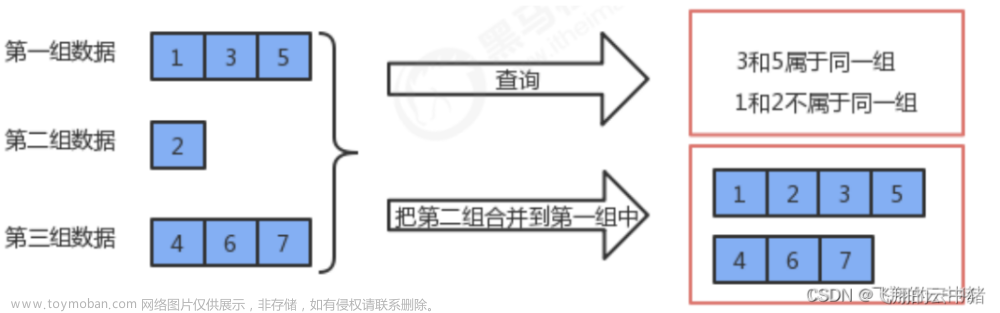
Union-Find 问题:给定 \(n\) 个元素,最初每个元素在一个集合中,有两种操作,union 表示合并两个集合,find 表示查询某个特定元素所在的集合。
并查集是一种数据结构。其为每个集合寻找一个代表元,代表元可以是任意的,也可以随操作变化,但需要满足任何时刻一个集合的代表元是确定且唯一的。数据结构支持 MakeSet, Find, Union 三种操作,表示新建一个仅包含一个元素的集合、寻找一个集合的代表元、合并两个元素所在的集合。
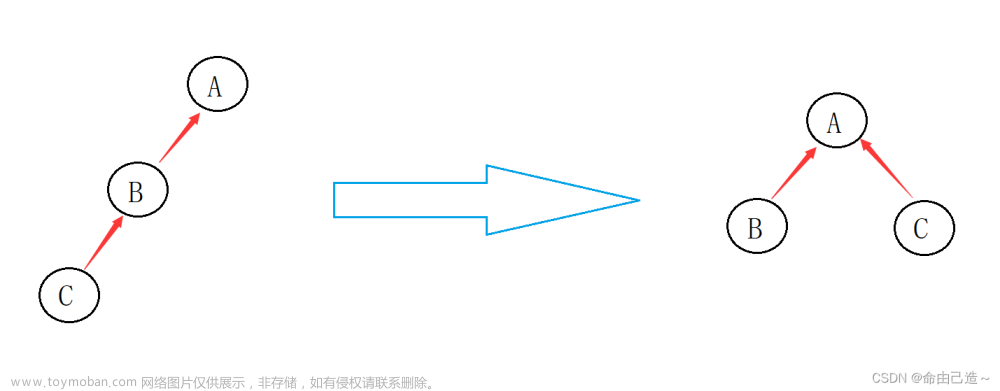
Up-tree 是并查集最常用的实现方式,其将每个集合的元素维护为一棵有根树,将根作为这个集合的代表元,Union 时通过将一个根连到另一个根上将两棵树合并为一棵,Find 时不断爬父亲找根即可。
设 \(n\) 为元素个数,\(m\) 为操作次数。
Union 总是 \(O(1)\) 的,关键在于 Find。什么都不做是 \(O(n)\) 的。有两种优化,按秩合并和路径压缩。按秩合并是守序善良的 \(\log\) 数据结构。带按秩合并的路径压缩是难分析的。
需要注意的是 Find 一个点的复杂度为这个点所在集合改变代表元的次数。
有两种常用的秩的定义方法,高度 Height 和重量 Weight。合并时总是将秩小的根连到秩大的根上。如果是高度,则秩增大 \(1\) 当且仅当两个集合秩相同,因此可以归纳证明秩为 \(k\) 至少需要 \(2^k\) 个点(达到下界的是二项树),因此每个点至多更换 \(\log\) 次代表元,复杂度为单次严格 \(O(\log n)\)。重量同理。
路径压缩在每次 Find 时将涉及到的一条链打散,所有点直接挂在根上,这个操作不会额外增加复杂度。
如果按秩合并和路径压缩同时使用,那基于高度的秩将不方便维护。不过我们可以修改其定义,Find 时秩不改变,Union 时只有两者秩相同则新的根的秩增加一,旧的不变,否则小的合并到大的上,两者都不变。我们来分析其复杂度。
随着操作进行,对于每个 \(x\),\(\mathrm{rank}(x)\) 只增不减。当 \(x\) 不为根时,\(\mathrm{rank}(x)\) 不再改变。如果 \(y\) 是 \(x\) 的父亲,\(\mathrm{rank}(y) > \mathrm{rank}(x)\)。对于 \(\mathrm{rank} \geq r\) 的结点任何时候至多 \(\frac {\min(n, m)}{2^r}\) 个。
令 \(T(m, r)\) 表示 \(m\) 个操作,秩 \(< r\) 的复杂度,令 \(s\) 为秩的一个阈值。考虑路径压缩时 \(x\) 被挂在了新父亲 \(y\) 上。
- \(\mathrm{rank}(x), \mathrm{rank}(y) < s\),则归档到 \(T(m_0, s)\) 中。
- \(\mathrm{rank}(x), \mathrm{rank}(y) \geq s\),共涉及 \(\frac m{2^s}\) 个结点,总复杂度 \(T(m_1, r) = O(\frac{m}{2^s}r)\)。
-
\(\mathrm{rank}(x) < s \leq \mathrm{rank}(y)\),再分两种情况
- \(\mathrm{rank}(\mathrm{parent}(x)) < s\),则经过一次操作后 \(\mathrm{rank}(\mathrm{parent}(x)) = \mathrm{rank}(y) \geq s\),因此总复杂度 \(O(m)\)。
- \(\mathrm{rank}(\mathrm{parent}(x)) \geq s\),每次 Find 只会有一个这样的 \(x\),因此为每次 Find 增加 \(O(1)\)。
所以,我们得到
取 \(s = \log r\),则有
因此,只需要递归 \(\log^* r\) 层,所以
回到
- \(\mathrm{rank}(x), \mathrm{rank}(y) \geq s\),共有 \(\frac m{2^s}\) 个结点,总复杂度 \(T(m_1, r) = O(\frac{m}{2^s}r)\)。
我们将其优化为了 \(O(\frac{m}{2^s}\log^* r)\)。因此重新写
令 \(s = \log^{**}r\),即迭代 \(\log^*\) 多少次 \(r\) 后到一个常数,则可以得到
等等等等,所以对任何常数 \(k\),
但是由于递归是非常数,或称 \(\omega(1)\) 轮的,所以不能直接认最终复杂度为 \(O(m)\),一个常数经过 \(\omega(1)\) 轮递归后可能叠加为 \(\omega(1)\)。我们需要精确分析常数。
最初
令 \(s = \log r\),则
以此类推,最终得到
令 \(k = \alpha(n)\),\(\log^{*^{(k)}} r\) 归为常数,最终复杂度为 \(O(m \alpha(n))\)。
其中 \(\alpha\) 为反阿克曼函数,\(\alpha(n) = \min\{k \mid A(k, 1) \geq n\}\),其中 \(A\) 为阿克曼函数。阿克曼函数是这样定义的:
可知其是将上一个值 \(A(m, n - 1)\) 作为在第 \(m - 1\) 行的递归轮数,因此 \(m\) 充当的是递归形式的阶次。
其比任何多项式和指数函数增长得都要快。因此 \(\alpha(n)\) 比任何 \(\log^{***\ldots **}\) 增长得都要慢。但其不是常数,\(\lim_{n \to +\infty}\alpha(n) \to +\infty\)。
不难发现 \(\log^{*^{(k)}}\) 表示的是经过多少次 \(k - 1\) 阶递归能到一个常数,和 \(A\) 的定义恰好相对。\(\alpha(n) \approx \min\left\{k \mid \log^{*^{(k)}} \leq 3\right\}\)。
-
Up-tree 实现的并查集复杂度为 \(\Omega(m \alpha(n))\)。[Tarjan, '75]
-
Union-Find 问题的下界为 \(\Omega(\alpha(n))\)。[Fredman, Saks '89]
接下来介绍另一个 \(\alpha\) 在复杂度中出现的问题,区间半群查询。
有 \(n\) 个元素 \(A_1, A_2, \ldots, A_n \in (G, +)\) 排成一行,每次查询 \(i, j\),求 \(\sum_{q=i}^j A_q\)。半群意味着不能使用前缀和相减(因为没有加法逆元)等手段,只有加法封闭和结合律两条性质。要求使用尽可能少的存储量,使得每次查询时只使用至多 \(k\) 次加法。设 \(S_k(n)\) 表示最少存储量。
对 \(S_1(n)\),序列分治得到
对 \(S_3(n)\),递归四毛子,第一层块大小 \(B = \log n\),对每个块存前后缀,块间用 \(S_1\),块内递归 \(S_3\) 得到
其和之前的形式类似。可得
假设
其中 \(f(n)\) 为块大小,满足对 \(n\) 不降,则
归纳可得
因此文章来源:https://www.toymoban.com/news/detail-710976.html
更进一步地有文章来源地址https://www.toymoban.com/news/detail-710976.html
- 对于 \(O(\alpha(n))\) 次加法,\(O(n)\) 空间 [Yao; Chazelle, Rosenberg]。
到了这里,关于[算法分析与设计] 3. 并查集分析与反阿克曼函数的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!