20.2 OpenSSL 非对称RSA加解密算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了20.2 OpenSSL 非对称RSA加解密算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

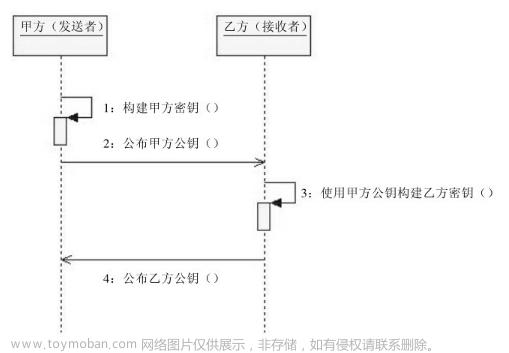
RSA算法是一种非对称加密算法，由三位数学家Rivest、Shamir和Adleman共同发明，以他们三人的名字首字母命名。RSA算法的安全性基于大数分解问题，即对于一个非常大的合数，将其分解为两个质数的乘积是非常困难的。

RSA算法是一种常用的非对称加密算法，与对称加密算法不同，RSA算法使用一对非对称密钥，分别为公钥和私钥，公钥和私钥是成对生成的，公钥可以公开，用于加密数据和验证数字签名，而私钥必须保密，用于解密数据和生成数字签名。因此，RSA算法的使用场景是公钥加密、私钥解密，或者私钥加密、公钥解密。

OpenSSL库中提供了针对此类算法的支持，但在使用时读者需要自行生成公钥与私钥文件，在开发工具包内有一个openssl.exe程序，该程序则是用于生成密钥对的工具，当我们需要使用非对称加密算法时，则可以使用如下命令生成公钥和私钥。

生成私钥: openssl genrsa -out rsa_private_key.pem 1024
生成公钥: openssl rsa -in rsa_private_key.pem -pubout -out rsa_public_key.pem

读者执行上述两条命令后即可得到rsa_private_key.pem私钥，以及rsa_public_key.pem公钥，如下图所示；

20.2 OpenSSL 非对称RSA加解密算法

在使用非对称加密时，读者需要分别导入所需要的头文件，这其中就包括了rsa.h用于处理加密算法的库，以及pem.h用于处理私钥的库，这两个库是使用RSA时必须要导入的。

#include <iostream>
#include <string>
#include <openssl/err.h>
#include <openssl/rsa.h>
#include <openssl/pem.h>
#include <openssl/crypto.h>

extern "C"
{
#include <openssl/applink.c>
}

#pragma comment(lib,"libssl.lib")
#pragma comment(lib,"libcrypto.lib")

20.2.1 公钥加密私钥解密

RSA公钥用于加密数据和验证数字签名，私钥用于解密数据和生成数字签名，通常用于公钥加密、私钥解密的场景，具有较高的安全性，但加密和解密速度较慢，因此通常采用一种混合加密方式，即使用RSA算法加密对称加密算法中的密钥，再使用对称加密算法加密数据，以保证数据的机密性和加密解密的效率。

首先我们来实现公钥加密功能，如下Public_RsaEncrypt函数，该函数接受两个参数，分别是需要加密的字符串以及公钥文件，代码中首先通过fopen()打开一个公钥文件，并通过PEM_read_RSA_PUBKEY函数读入并初始化公钥文件，接着调用RSA_public_encrypt该函数主要用于实现公钥加密，当加密成功后返回加密后的文本内容，类型是字符串。

// 公钥加密
std::string Public_RsaEncrypt(const std::string& str, const std::string& path)
{
    RSA* rsa = NULL;
    FILE* file = NULL;
    char* ciphertext = NULL;
    int len = 0;
    int ret = 0;

    file = fopen(path.c_str(), "r");
    if (file == NULL)
    {
        return std::string();
    }

    rsa = PEM_read_RSA_PUBKEY(file, NULL, NULL, NULL);
    if (rsa == NULL)
    {
        ERR_print_errors_fp(stdout);
        fclose(file);
        return std::string();
    }

    len = RSA_size(rsa);
    ciphertext = (char*)malloc(len + 1);
    if (ciphertext == NULL)
    {
        RSA_free(rsa);
        fclose(file);
        return std::string();
    }
    memset(ciphertext, 0, len + 1);

    ret = RSA_public_encrypt(str.length(), (unsigned char*)str.c_str(), (unsigned char*)ciphertext, rsa, RSA_PKCS1_PADDING);
    if (ret < 0)
    {
        ERR_print_errors_fp(stdout);
        free(ciphertext);
        RSA_free(rsa);
        fclose(file);
        return std::string();
    }

    std::string s(ciphertext, ret);
    free(ciphertext);
    RSA_free(rsa);
    fclose(file);
    return s;
}

与公钥加密方法类似，Private_RsaDecrypt函数用于使用私钥进行解密，该函数接受两个参数，第一个参数是加密后的字符串数据，第二个参数则是私钥的具体路径，函数中通过PEM_read_RSAPrivateKey实现对私钥的初始化，并通过RSA_private_decrypt函数来实现对特定字符串的解密操作。

// 私钥解密
std::string Private_RsaDecrypt(const std::string& str, const std::string& path)
{
    RSA* rsa = NULL;
    FILE* file = NULL;
    char* plaintext = NULL;
    int len = 0;
    int ret = 0;

    file = fopen(path.c_str(), "r");
    if (file == NULL)
    {
        return std::string();
    }

    rsa = PEM_read_RSAPrivateKey(file, NULL, NULL, NULL);
    if (rsa == NULL)
    {
        ERR_print_errors_fp(stdout);
        fclose(file);
        return std::string();
    }

    len = RSA_size(rsa);
    plaintext = (char*)malloc(len + 1);
    if (plaintext == NULL)
    {
        RSA_free(rsa);
        fclose(file);
        return std::string();
    }
    memset(plaintext, 0, len + 1);

    ret = RSA_private_decrypt(str.length(), (unsigned char*)str.c_str(), (unsigned char*)plaintext, rsa, RSA_PKCS1_PADDING);
    if (ret < 0)
    {
        ERR_print_errors_fp(stdout);
        free(plaintext);
        RSA_free(rsa);
        fclose(file);
        return std::string();
    }
    std::string s(plaintext, ret);

    free(plaintext);
    RSA_free(rsa);
    fclose(file);
    return s;
}

这两段代码的调用也非常容易，如下代码片段则分别实现了对text字符串的加密与解密功能，使用公钥加密，使用私钥解密。

int main(int argc, char* argv[])
{
  std::string text = "hello lyshark";

  // 公钥加密
  std::string public_path = "d://rsa_public_key.pem";
  std::string encry = Public_RsaEncrypt(text, public_path);
  // std::cout << "加密后文本: " << encry << std::endl;

  // 私钥解密
  std::string private_path = "d://rsa_private_key.pem";
  std::string decry = Private_RsaDecrypt(encry, private_path);
  std::cout << "解密后文本: " << decry << std::endl;

  system("pause");
  return 0;
}

这段代码输出效果如下图所示；

20.2 OpenSSL 非对称RSA加解密算法文章来源地址https://www.toymoban.com/news/detail-711173.html

20.2.2 私钥加密公钥解密

在RSA算法中，私钥加密公钥解密并不是一种常见的使用方式，因为私钥是用于签名而不是加密的。通常的使用方式是，使用公钥加密，私钥解密，这样可以保证数据的机密性，只有拥有私钥的人才能解密数据，但在某些时候我们不得不将这个流程反过来，使用私钥加密并使用公钥解密。

私钥加密的封装代码如下所示，其中Private_RsaEncrypt用于实现私钥加密，该函数同样接受两个参数，分别是待加密字符串以及当前私钥路径，函数的核心部分是RSA_private_encrypt该函数可用于使用私钥对数据进行加密。

// 私钥加密
std::string Private_RsaEncrypt(const std::string& str, const std::string& path)
{
    RSA* rsa = NULL;
    FILE* file = NULL;
    char* ciphertext = NULL;
    int len = 0;
    int ret = 0;

    file = fopen(path.c_str(), "r");
    if (file == NULL)
    {
        return std::string();
    }
    rsa = PEM_read_RSAPrivateKey(file, NULL, NULL, NULL);

    if (rsa == NULL)
    {
        ERR_print_errors_fp(stdout);
        fclose(file);
        return std::string();
    }

    len = RSA_size(rsa);
    ciphertext = (char*)malloc(len + 1);
    if (ciphertext == NULL)
    {
        RSA_free(rsa);
        fclose(file);
        return std::string();
    }
    memset(ciphertext, 0, len + 1);

    ret = RSA_private_encrypt(str.length(), (unsigned char*)str.c_str(), (unsigned char*)ciphertext, rsa, RSA_PKCS1_PADDING);
    if (ret < 0)
    {
        ERR_print_errors_fp(stdout);
        free(ciphertext);
        RSA_free(rsa);
        fclose(file);
        return std::string();
    }

    std::string s(ciphertext, ret);
    free(ciphertext);
    RSA_free(rsa);
    fclose(file);
    return s;
}

公钥解密的实现方法与加密完全一致，代码中Public_RsaDecrypt函数用于实现公钥解密，其核心功能的实现依赖于RSA_public_decrypt这个关键函数。

// 公钥解密
std::string Public_RsaDecrypt(const std::string& str, const std::string& path)
{
    RSA* rsa = NULL;
    FILE* file = NULL;
    char* plaintext = NULL;
    int len = 0;
    int ret = 0;

    file = fopen(path.c_str(), "r");
    if (file == NULL)
    {
        return std::string();
    }

    rsa = PEM_read_RSA_PUBKEY(file, NULL, NULL, NULL);
    if (rsa == NULL)
    {
        ERR_print_errors_fp(stdout);
        fclose(file);
        return std::string();
    }

    len = RSA_size(rsa);
    plaintext = (char*)malloc(len + 1);
    if (plaintext == NULL)
    {
        RSA_free(rsa);
        fclose(file);
        return std::string();
    }
    memset(plaintext, 0, len + 1);

    ret = RSA_public_decrypt(str.length(), (unsigned char*)str.c_str(), (unsigned char*)plaintext, rsa, RSA_PKCS1_PADDING);
    if (ret < 0)
    {
        ERR_print_errors_fp(stdout);
        free(plaintext);
        RSA_free(rsa);
        fclose(file);
        return std::string();
    }
    std::string s(plaintext, ret);

    free(plaintext);
    RSA_free(rsa);
    fclose(file);
    return s;
}

有了上述方法，那么调用代码则变得很容易，如下所示，我们将text字符串使用私钥进行加密，并使用公钥进行解密。

int main(int argc, char* argv[])
{
  std::string text = "hello lyshark";

  // 私钥加密
  std::string private_path = "d://rsa_private_key.pem";
  std::string encry = Private_RsaEncrypt(text, private_path);
  // std::cout << "加密后文本: " << encry << std::endl;

  // 公钥解密
  std::string public_path = "d://rsa_public_key.pem";
  std::string decry = Public_RsaDecrypt(encry, public_path);
  std::cout << "解密后文本:" << decry << std::endl;

  system("pause");
  return 0;
}

这段代码输出效果如下图所示；

20.2 OpenSSL 非对称RSA加解密算法

到了这里，关于20.2 OpenSSL 非对称RSA加解密算法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！