动态规划——决策单调性优化DP 学习笔记
决策单调性
对于最优性问题,常有状态转移方程:\(f_i = \min/\max\{f_j\dots\}\),
形象的:如果 \(i\) 的最优转移点是 \(j\),\(i'\) 的最优转移点是 \(j'\),当 \(i<i'\) 时,有 \(j\le j'\),则称该 DP 问题具有决策单调性。
即:\(i\) 单增,其最优转移点单调不减。
如何发现一个转移方程具有决策单调性?打表。
使用
一、离线决策单调性
形如:\(f(i, j) = \min\limits_{k \le j}\{f(i-1, k)+\text{cost}(k,j)\}\),转移分层.
形象的:\(f(i, j)\) 表示将前 \(j\) 个物品分为 \(i\) 端的最小花费,则原式意为,枚举一个 \(k\) 个,将前 \(k\) 个分为 \(i-1\) 段,再加上后面这一段所需的花费。
那么此时,最 native 的算法是,三层循环枚举,时间复杂度就是 \(O(nm^2)\) 的。
决策单调性:设 \(k\) 为 \(f(i,j)\) 的最优转移点,\(k'\) 为 \(f(i, j')\) 的最优转移点,当 \(j<j'\) 时有 \(k\le k'\),则该 DP 具有决策单调性。
形象的:对于每一层(固定 \(i\) 不变),\(j\) 单增,其最优转移点(在 \(i-1\) 层上)单调不减。
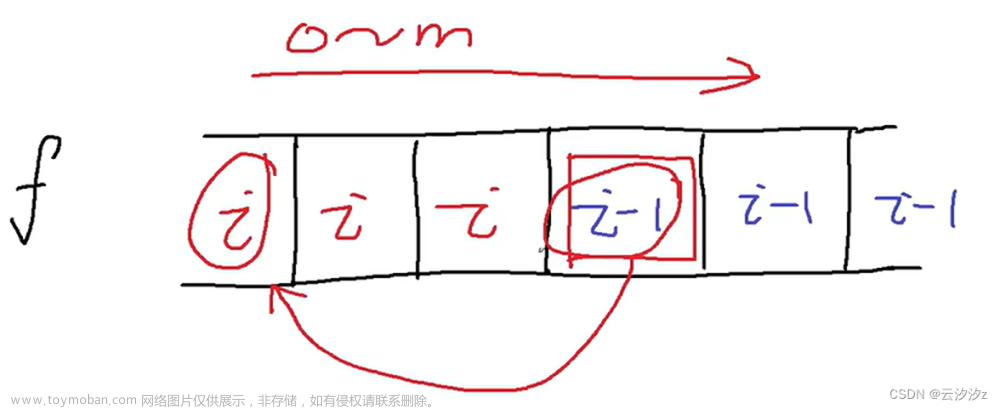
因此,我们可以一层一层的 DP,对于第 \(i\) 层,我们先算 \(f(i, \mathrm{mid})\),其中 \(\mathrm{mid} = m/2\);同时求出 \(f(i, \mathrm{mid})\) 的最优转移点 \(f(i-1, \mathrm{opt})\)。那么 \([1,i-1]\) 的最优转移点只能在 \(f(i-1,1\dots \mathrm{opt})\) 中取,\([i+1,n]\) 的最优转移点只能在 \(f(i-1,\mathrm{opt}\dots n)\) 中取。
如图:
递归下去,即:
\(s(i,l,r,p,q)\) 表示算 \(f(i,l\dots r)\) 且最优转移点只可能在 \(f(i-1,p\dots q)\)中,先算 \(f(i,\mathrm{mid})\) 的值(即枚举 \(p\) 到 \(q\)),求出最优转移点 \(\mathrm{opt}\)。
然后递归求解:\(s(i,l,r,p,q)\rightarrow\left\{\begin{array}{c}s(i,l,\mathrm{mid}-1,p,\mathrm{opt})\\s(i,\mathrm{mid}+1,r,\mathrm{opt},q)\end{array}\right.\).
则时间复杂度为 \(O(nm \log m)\)。
例题:CF321E Ciel and Gondolas.
点击查看代码
仅核心代码。
暴力:
inline int cost(const int x, const int y) {
return (s[y][y] - s[y][x - 1] - s[x - 1][y] + s[x - 1][x - 1]) >> 1;
} signed main() {
int n = ur, k = ur;
for (int i = 1; i <= n; ++i) for (int j = 1; j <= n; ++j) s[i][j] = ur + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
memset(f, 0x3f, sizeof f); for (int i = 0; i <= n; ++i) f[i][0] = 0;
for (int i = 1; i <= k; ++i) for (int j = 0; j <= n; ++j) {
for (int t = 0; t <= j; ++t) f[i][j] = min(f[i][j], f[i - 1][t] + cost(t + 1, j));
} printf("%d\n", f[k][n]);
return 0;
}
决策单调性优化:
inline int cost(const int x, const int y) {
return (s[y][y] - s[y][x - 1] - s[x - 1][y] + s[x - 1][x - 1]) >> 1;
} void solve(int i, int l, int r, int p, int q) {
if (l > r) return;
int j = l + r >> 1, opt = 0;
for (int t = p; t <= q && t <= j; ++t) {
int e = f[i - 1][t] + cost(t + 1, j);
if (f[i][j] > e) f[i][j] = e, opt = t;
}
solve(i, l, j - 1, p, opt);
solve(i, j + 1, r, opt, q);
} signed main() {
int n = rr, k = rr;
for (int i = 1; i <= n; ++i) for (int j = 1 ; j <= n; ++j) s[i][j] = rr + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
memset(f, 0x3f, sizeof f); f[0][0] = 0;
for (int i = 1; i <= k; ++i) solve(i, 0, n, 0, n);
printf("%d\n", f[k][n]);
return 0;
}
二、离线决策单调性
一维 DP,形如:\(f_r=\min\limits_{l=1}^{r-1}\{f_l+\text{cost}(l,r)\}\).
其决策单调性为 \(i\) 单增,其最优转移点 \(j\) 单调不见,比如:11122222244 这种。

没听懂 zhq 老师讲的,等着看 wzm 的回放。。。
三、区间 DP 决策单调性
对于最优化的区间 DP,设 \(d_{i,j}\) 为 \(f_{i,j}\) 的最优转移点,具有决策单调性的条件为 \(d_{l,r-1} \le d_{l,r} \le d_{l+1,r}\)。
求解方法:按长度枚举区间;计算 \(f_{lr}\) 的时候,从 \(d_{l,r-1}\) 枚举到 \(d_{l+1,r}\)。
时间复杂度:\(O(n^2)\),神奇的证明(\(\text{By zhq}\))如图:

题单
见:https://www.luogu.com.cn/training/386809文章来源:https://www.toymoban.com/news/detail-711388.html
Reference
[1] https://oi-wiki.org/dp/opt/quadrangle/
[2] https://www.cnblogs.com/lnzwz/p/12444390.html
[3] https://www.cnblogs.com/lhm-/p/12229791.html
[4] https://www.luogu.com.cn/blog/command-block/dp-di-jue-ce-dan-diao-xing-you-hua-zong-jie文章来源地址https://www.toymoban.com/news/detail-711388.html
到了这里,关于动态规划——决策单调性优化DP 学习笔记的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!