【数据结构】6.搜索树-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】6.搜索树。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1.二叉搜索树

1.1 定义

二叉搜索树：

一棵非空的二叉搜索树每个元素都有一个关键字，并且任意两个元素的关键字不同，所有关键字都是唯一的
根节点的左子树小于根节点的关键字
根节点的右子树大于根节点的关键字
左右子树也是二叉搜索树

【数据结构】6.搜索树

索引二叉搜索树：

　　源于普通的二叉搜索树，在每个节点中添加一个 leftSize 字段，用来保存该节点左子树的元素个数。

【数据结构】6.搜索树

1.2 二叉搜索树的操作和实现

1.2.1 搜索

根据搜索元素的 theKey 对应向左孩子或右孩子移动寻找即可，时间复杂度为O(height)

【数据结构】6.搜索树

template<class K, class E>
pair<const K, E>* binarySearchTree<K, E>::find(const K& theKey) const
{// 返回关键字时K的元素指针
   // 从根节点 p 开始搜索，寻找关键字为 theKey 的元素
    binaryTreeNode<pair<const K, E> >* p = root;
    while (p != NULL)
        // 检查元素
        if (theKey < p->element.first)
            p = p->leftChild;
        else
            if (theKey > p->element.first)
                p = p->rightChild;
            else // 找到匹配的元素
                return &p->element;

    // 未找到匹配的元素
    return NULL;
}

1.2.2 插入

　　使用 pp 指针记录 p 指针的双亲节点，p 指针不断查找应该插入的位置

p 指针指向空时，说明该插入到该位置。判断插入元素 theKey 和 pp 指针的大小关系插入该元素
p 指针找到相同的 theKey 时，更新该节点的 value

【数据结构】6.搜索树

template<class K, class E>
void binarySearchTree<K, E>::insert(const pair<const K, E>& thePair)
{// 插入thePair节点，如果存在相同的Key则覆盖元素
    binaryTreeNode<pair<const K, E> >* p = root;
    binaryTreeNode<pair<const K, E> >* pp = NULL;

    // 如果循环结束未找到该元素, 则pp元素就是该元素的父节点
    while (p != NULL)
    {// 检查元素p
        pp = p;
        // 将p移动到它的孩子节点
        if (thePair.first < p->element.first)
            p = p->leftChild;
        else
            if (thePair.first > p->element.first)
                p = p->rightChild;
            else
            {// 如果有相同的key, 覆盖旧的值
                p->element.second = thePair.second;
                return;
            }
    }

    // 为thePair创建一个节点, 然后与pp连接
    binaryTreeNode<pair<const K, E> >* newNode = new binaryTreeNode<pair<const K, E> >(thePair);
    if (root != NULL) // 判断树是否是空
        if (thePair.first < pp->element.first)
            pp->leftChild = newNode;
        else
            pp->rightChild = newNode;
    else
        root = newNode; // 直接将节点作为根节点
    treeSize++;
}

1.2.3 删除

　　删除分三种情况

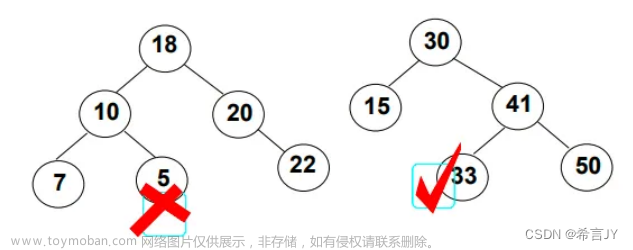
要删除的节点没有孩子节点：如左图所示，这种情况只需要找到该节点释放内存空间，并将双亲节点的右孩子指针置为空即可
要删除的节点只有一个孩子节点：如右图所示，这种情况只需要将该节点内存空间释放，并且将元素15 的左孩子连接到元素12 的孩子节点即可

【数据结构】6.搜索树

要删除的节点有两个孩子节点，且要更换位置的节点没有孩子节点。我们需要在要删除的节点的左孩子中，向右寻找到最大的元素做替换，将元素14 重新连接元素12 和元素18 构建一个新的树，并重新连接到元素20 的左孩子位置，最后释放元素14的内存（这种情况实际上转换为构建一棵树，然后删除14，且14没有孩子节点）

【数据结构】6.搜索树

要删除的节点有两个孩子节点，且要更换位置的节点有一个孩子节点。我们需要在要删除的节点的左孩子中，向右寻找到最大的元素做替换，将元素14 重新连接元素12 和元素18 构建一个新的树，并重新连接到元素20 的左孩子的位置，然后把元素14 的孩子连接到元素14 的双亲节点处，释放元素14 的内存空间（这种情况实际上转换为构建一棵树，然后删除14，且14有一个孩子节点）

【数据结构】6.搜索树文章来源地址https://www.toymoban.com/news/detail-711580.html

template<class K, class E>
void binarySearchTree<K, E>::erase(const K& theKey)
{// 删除关键字为 theKey 的节点

    // 查找关键字为 theKey 的节点
    binaryTreeNode<pair<const K, E> >* p = root;    // p 是要删除的节点
    binaryTreeNode<pair<const K, E> >* pp = NULL;   // pp 是 p 的双亲
    while (p != NULL && p->element.first != theKey)
    {// p移动到它的孩子节点
        pp = p;
        if (theKey < p->element.first)
            p = p->leftChild;
        else
            p = p->rightChild;
    }
    if (p == NULL)
        return; // 未找到则直接结束

    // 找到一个 s 元素替换要删除的元素 p, 然后用元素 s 构建一棵树
    // 接下来转换为删除元素 s 的操作, s 只有左孩子或者没有孩子
    if (p->leftChild != NULL && p->rightChild != NULL)
    {
        binaryTreeNode<pair<const K, E>>* s = p->leftChild; // s: 在 p 的左孩子中找到最大的元素
        binaryTreeNode<pair<const K, E>>* ps = p;           // ps: s 的双亲
        while (s->rightChild != NULL)
        {
            ps = s;
            s = s->rightChild;
        }

        // 用元素 s 构建一棵树, 替代元素 p 的位置
        binaryTreeNode<pair<const K, E> >* q = new binaryTreeNode<pair<const K, E>> (s->element, p->leftChild, p->rightChild);

        // 如果要删除的没有双亲, 根节点就是 q, 否则把孩子节点更换为 q
        if (pp == NULL) { root = q; }
        else if (p == pp->leftChild) { pp->leftChild = q; }
        else { pp->rightChild = q; }

        // 如果 s 恰好是要删除元素 p 的下一个节点, 单独处理一下
        if (ps == p) { pp = q; }
        else { pp = ps; }

        // 释放元素 p 的空间, 把 p 的指针指向 s, 接下来的工作是删除 s
        delete p;
        p = s;
    }

    // 下面的情况: 元素 p 只有一个孩子或者没有孩子
    // 指针 c 指向了元素 p 的孩子或者 NULL
    binaryTreeNode<pair<const K, E> >* c;
    if (p->leftChild != NULL) { c = p->leftChild; }
    else if (p->leftChild != NULL) { c = p->rightChild; }
    else { c = NULL; }

    // 如果要删除的 p 是根节点
    if (p == root)
        root = c;
    else
    {// 否则将 pp 的孩子置为 p
        if (p == pp->leftChild)
            pp->leftChild = c;
        else pp->rightChild = c;
    }
    treeSize--;
    delete p;
}