【数据结构】1.线性表的数组描述和链式描述-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】1.线性表的数组描述和链式描述。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1. 线性表抽象类

#pragma once
template <class T>
class LinearList
{
public:
    // 线性表是否为空
    virtual bool empty() const = 0;
    // 线性表大小
    virtual int size() const = 0;
    // 根据ID获取线性表元素
    virtual T& get(int theIndex) const = 0;
    // 根据元素获取元素对应ID
    virtual int indexOf(const T& theElement) const = 0;
    // 删除ID处的元素
    virtual void erase(int theIndex) = 0;
    // 在ID处插入元素
    virtual void insert(int theIndex, const T& theElement) = 0;
    // 输出线性表
    virtual void output() = 0;
};

2. 线性表的数组描述

#include"linearList.h"
#include<iostream>
using namespace std;

template<class T>
class ArrayList :public LinearList<T>
{
protected:
    T* element;                                // 线性表元素指针
    int arrayLength;                        // 容量
    int listSize;                            // 元素个数
    bool checkIndex(int theIndex) const;    // 检查索引是否有效
    void changeLength();                    // 扩充数组长度

public:
    // 构造函数
    ArrayList(int initialCapacity = 10);
    // 拷贝构造函数
    ArrayList(const ArrayList<T>& theList);
    // 析构函数
    ~ArrayList() 
    {
        delete[] element;
    }

    // 线性表是否为空
    bool empty() const { return listSize == 0; }

    // 线性表大小
    int size() const { return listSize; }

    // 线性表容量
    int capacity() const { return arrayLength; }

    // 根据ID获取线性表元素
    T& get(int theIndex) const;

    // 根据元素获取元素对应ID
    int indexOf(const T& theElement) const;

    // 删除ID处的元素
    void erase(int theIndex);

    // 在ID处插入元素
    void insert(int theIndex, const T& theElement);

    // 输出线性表
    void output();

};


// 构造函数
template<class T>
ArrayList<T>::ArrayList(int initialCapacity)
{
    if (initialCapacity < 1) 
    {
        cout << "初始化容量必须大于0" << endl;
        return;
    }
    this->arrayLength = initialCapacity;
    this->element = new T[arrayLength];
    listSize = 0;
}

// 复制构造函数
template<class T>
ArrayList<T>::ArrayList(const ArrayList<T>& theList)
{
    this->arrayLength = theList.arrayLength;
    this->listSize = theList.listSize;
    this->element = new T[arrayLength];
    copy(theList.element, theList.element + listSize, element);
}

// 越界, false 表示越界, true 表示没有越界
template<class T>
bool ArrayList<T>::checkIndex(int theIndex) const
{
    bool ret = !(theIndex < 0 || theIndex > listSize);
    return ret;
}


// 获取元素
template<class T>
T& ArrayList<T>::get(int theIndex) const
{
    if (checkIndex(theIndex))
    {
        return element[theIndex];
    }
}

// 根据元素获取ID
template<class T>
int ArrayList<T>::indexOf(const T& theElement) const
{
    int theIndex = (int)find(element, element + listSize, theElement);
    return theIndex == listSize ? -1 : (theIndex-(int)element)/sizeof(T);
}

// 删除ID处元素
template<class T>
void ArrayList<T>::erase(int theIndex)
{
    if (checkIndex(theIndex))
    {
        copy(element + theIndex + 1, element + listSize, element + theIndex);
        element[--listSize].~T();
    }
}

// 扩充数组长度
template<class T>
void ArrayList<T>::changeLength()
{
    T* temp = new T[arrayLength * 2];
    copy(element, element + arrayLength, temp);
    delete[] element;
    element = temp;
    arrayLength = 2 * arrayLength;
}


// 在ID处插入元素
template<class T>
void ArrayList<T>::insert(int theIndex, const T& theElement)
{
    if (!checkIndex(theIndex))
    {
        cout << "无效索引" << endl;
        return;
    }
    if (listSize == arrayLength)
    {
        changeLength();
    }
    copy_backward(element + theIndex, element + listSize, element + listSize + 1);
    element[theIndex] = theElement;
    listSize++;
}

// 输出线性表
template<class T>
void ArrayList<T>::output()
{
    for (int i = 0; i < listSize; i++)
    {
        cout << element[i] << " ";
    }
    cout << endl;
}

3. 线性表的链式描述

3.1 结点结构体

#pragma once
#include<iostream>
using namespace std;
template <class T>
struct ChainNode
{
    // 数据成员
    T element;
    ChainNode<T>* next;

    // 方法
    ChainNode() {}
    ChainNode(const T& element)
    {
        this->element = element;
    }
    ChainNode(const T& element, ChainNode<T>* next)
    {
        this->element = element;
        this->next = next;
    }
};

3.2 线性表实现

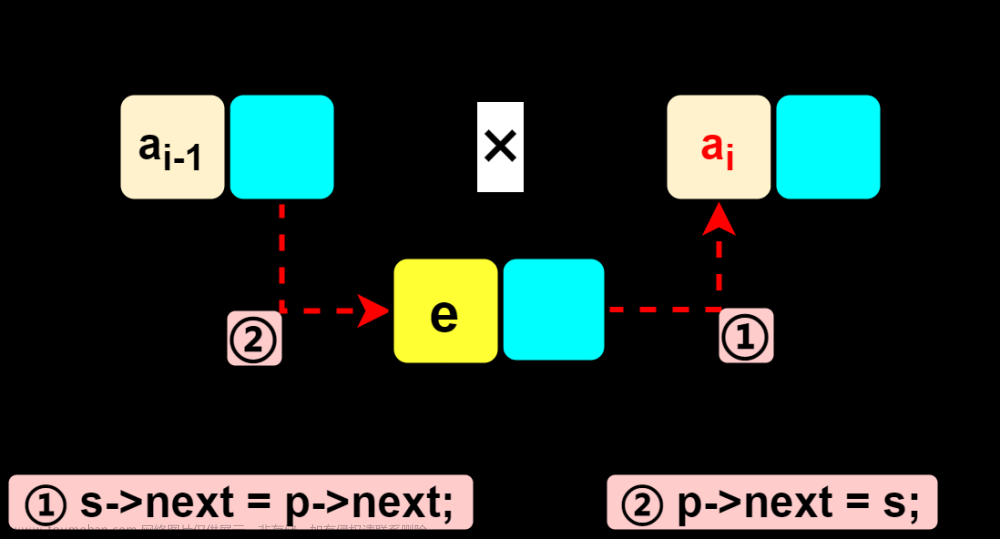
#include"linearList.h"
#include"chianNode.h"
#include<iostream>
using namespace std;
template<class T>
class Chain :public LinearList<T>
{
protected:
    ChainNode<T>* firstNode;
    int listSize;
    bool checkIndex(int theIndex) const;

public:
    Chain(int initialCapacity = 10);
    Chain(const Chain<T>&);
    ~Chain();

    bool empty() const { return listSize == 0; };
    // 线性表大小
    int size() const { return listSize; }
    // 根据ID获取线性表元素
    T& get(int theIndex) const;
    // 根据元素获取元素对应ID
    int indexOf(const T& theElement) const;
    // 删除ID处的元素
    void erase(int theIndex);
    // 在ID处插入元素
    void insert(int theIndex, const T& theElement);
    // 输出线性表
    void output();
};

// 普通的构造函数
template<class T>
Chain<T>::Chain(int initialCapacity)
{
    if (initialCapacity < 1)
    {
        cout << "初始容量设置必须大于0" << endl;
    }
    firstNode = NULL;
    listSize = 0;
}

// 拷贝构造函数
template<class T>
Chain<T>::Chain(const Chain<T>& theList)
{
    listSize = theList.listSize;
    if (listSize == 0)
    {
        firstNode = NULL;
        return;
    }
    ChainNode<T>* sourceNode = theList.firstNode;
    firstNode = new ChainNode<T>(sourceNode->element);
    sourceNode = sourceNode->next;
    ChainNode<T>* targetNode = firstNode;
    while (sourceNode != NULL)
    {
        targetNode->next = new ChainNode<T>(sourceNode->element);
        targetNode = targetNode->next;
        sourceNode = sourceNode->next;
    }
    targetNode->next = NULL;
}

// 析构函数
template<class T>
Chain<T>::~Chain()
{
    while (firstNode != NULL)
    {
        ChainNode<T>* nextNode = firstNode->next;
        delete firstNode;
        firstNode = nextNode;
    }
}

template<class T>
T& Chain<T>::get(int theIndex) const
{
    if (checkIndex(theIndex))
    {
        ChainNode<T>* currentNode = firstNode;
        for (int i = 0; i < theIndex; i++)
        {
            currentNode = currentNode->next;
        }
        return currentNode->element;
    }
}

template<class T>
int Chain<T>::indexOf(const T& theElement) const
{
    ChainNode<T>* currentNode = firstNode;
    int index = 0;
    while (currentNode->element != theElement && currentNode != NULL)
    {
        currentNode = currentNode->next;
        index++;
    }
    return currentNode == NULL ? -1 : index;
}

template<class T>
void Chain<T>::erase(int theIndex)
{
    if (checkIndex(theIndex))
    {
        ChainNode<T>* deleteNode;
        if (theIndex == 0)
        {
            deleteNode = firstNode;
            firstNode = firstNode->next;
        }
        else if (theIndex < listSize - 1)
        {
            ChainNode<T>* p = firstNode;
            for (int i = 0; i < theIndex - 1; i++)
            {
                p = p->next;
            }
            deleteNode = p->next;
            p->next = p->next->next;
        }
        else
        {
            ChainNode<T>* p = firstNode;
            for (int i = 0; i < theIndex; i++)
            {
                p = p->next;
            }
            deleteNode = p;
            p->next = NULL;
        }
        listSize--;
        delete deleteNode;
    }
}

template<class T>
void Chain<T>::insert(int theIndex, const T& theElement)
{
    if (checkIndex(theIndex))
    {
        if (theIndex == 0)
        {
            firstNode = new ChainNode<T>(theElement, firstNode);
        }
        else
        {
            ChainNode<T>* p = firstNode;
            for (int i = 0; i < theIndex - 1; i++)
            {
                p = p->next;
            }
            p->next = new ChainNode<T>(theElement, p->next);
        }
        listSize++;
    }
}


template<class T>
void Chain<T>::output()
{
    ChainNode<T>* currentNode = firstNode;
    while (currentNode != NULL)
    {
        cout << currentNode->element << " ";
        currentNode = currentNode->next;
    }
    cout << endl;
}

template<class T>
bool Chain<T>::checkIndex(int theIndex) const
{
    bool ret = !(theIndex < 0 || theIndex > listSize);
    return ret;
}