二分查找结果总是不对？一文帮你解决二分查找的边界问题&&数组移除元素太耗时间，双指针法为你打开新世界的大门，降时间复杂度为O（n）-Toy模板网

这篇具有很好参考价值的文章主要介绍了二分查找结果总是不对？一文帮你解决二分查找的边界问题&&数组移除元素太耗时间，双指针法为你打开新世界的大门，降时间复杂度为O（n）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

前言

可能有粗心写的不正确的地方，或者因为技术有限写得不好的地方，欢迎大家批评指正，文章中给出的代码是本人自己写的leetcode中的代码，是代码的核心部分，如果放到本地编译器中，可能要加入mian()函数等内容。

题目1 二分查找

LeetCode704二分查找

题目要点

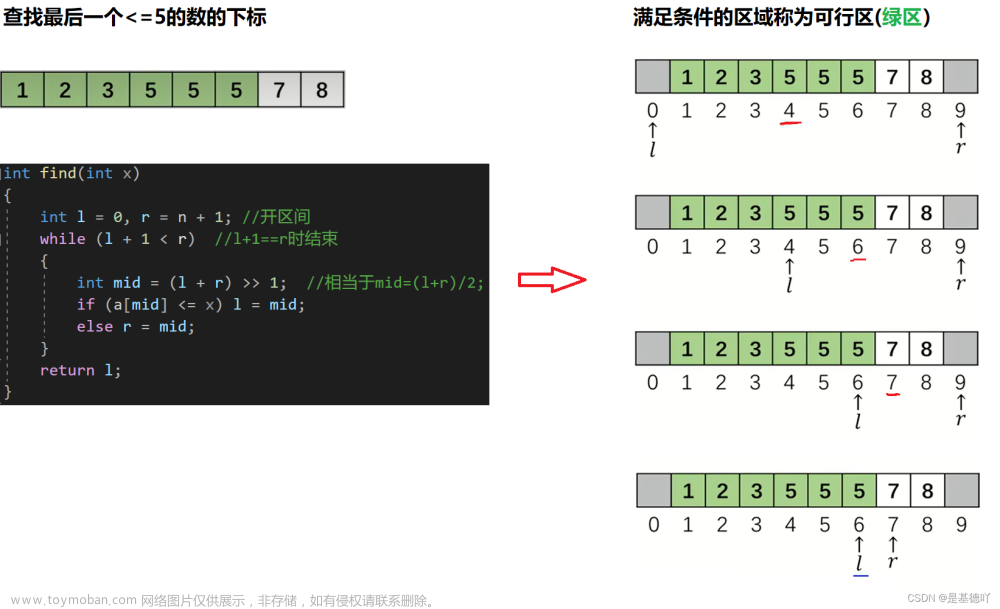
二分查找的思路非常简单，也就是我们常说的折半查找，比较经典的生活中的例子就是我们平时玩的猜数游戏，我们都知道，当给定一个数字范围的时候，我们应该先去猜它的正中间，这样就可以直接缩小一半的范围，二分查找用的就是这个原理，它的思路大体（左闭右闭）如下图所示：
二分查找结果总是不对？一文帮你解决二分查找的边界问题&&数组移除元素太耗时间，双指针法为你打开新世界的大门，降时间复杂度为O（n）

我们可以知道，二分查找的思路非常简单，但是写的时候却经常容易漏洞百出，这是为什么呢？一方面可能是因为我们对语法不太熟悉，另一方面可能是因为，对于边界的把控不好，为此，我们来讨论二分查找的边界问题，分为以下两种情况，我们对比着来看：

1.左闭右闭[left,right]

源代码如下：

	int n=nums.size();
        int left=0;
        int right=n-1; //right是第一个要注意的边界点
        int middle;
        while(left<=right) //while循环是第二个要注意的边界点
        {
            middle=(right+left)/2;
            if(target>nums[middle])
            {
                left=middle+1;
            }
            else if(target<nums[middle])
            {
                right=middle-1; //right和mid的赋值是第三个要注意的边界点
            }
            else if(target==nums[middle])
            return middle;
        }
        return -1;

1.左开右闭（left,right]

源代码如下：

    int n=nums.size();
    int left=0;
    int right=n; //right是第一个要注意的边界点
    int mid;
    while(left<right) //while循环是第二个要注意的边界点
    {
        mid=(left+right)/2;
        if(target==nums[mid])
        return mid;
        else if(target<nums[mid])
        {
            right=mid; //right和mid的赋值是第三个要注意的边界点
        }
        else if(target>nums[mid])
        {
            left=mid+1;
        }
    }
    return -1;

注意！！！

首先看right，可以这样理解，比较的时候要取到所有元素，所以闭区间只需要把下标都取到即可，而开区间需要再往后取一位，这样才能保证取到了数组中的所有元素。
其次看while循环语句，我们在进行循环时，要保证区间端点是合理的，当闭区间两端相等时，可以去到该元素，例如[a,a]，就可以取到a这个元素，但是半开半闭区间却不行，例如[a,a)就是一个不合法的区间，这也就决定了while循环中要不要加等号。
当通过判断 else if(target<nums[mid]) 进入right和mid的赋值时，说明mid不是要取的值，这个时候下一个区间不应该再有mid这个数字，开区间直接把右端点改为mid即可，而闭区间需要改为mid-1。

所犯错误

我在写的时候犯了一些很蠢的错误，不太具有参考价值，不过还是记录下来：

1.把数组名写错了，没错，你没听错，就是把nums[mid]写成a[mid]了。
2.忘记定义n了，这个题型大家在刷题的时候一定要看清楚Leetcode里面给了些什么没给什么。

题目2 移除数组元素

LeetCode27移除元素

题目要点

移除元素一共有两个方法，分别是暴力解法和双指针法，下面我们将一一介绍：

1.暴力解法

所谓暴力解法，也就是我们初学数组时最常用的方法，找到要删除的元素的下标，把该元素删除，并把后面的元素往前移动，这种方法就不多赘述，但要注意在进行一个for循环之后的i--操作，以下是LeedCode源代码：

int n=nums.size();
        for(int i=0;i<n;i++)
        {
            if(nums[i]==val)
            {
                for(int j=i;j<n-1;j++)
                {
                    nums[j]=nums[j+1];
                }
                i--; //注意这里
                n--;
            }
        }
        printf("%d, nums = [",n);
        for(int i=0;i<n;i++)
        printf("%d,",nums[i]);
        printf("]");
        return n;

这里的i--操作是因为，执行完这个循环体后，又一次进入最外层的for循环，此时位于位置i的数字还没有检查，但是最外层for循环要进行i++操作，为了检测当前i位置的新数字，要先进行i--的操作，例如数组[1,2,3,4,4,5],假设要删去4，第一次删除是下标为3，也就是第一个4，但是经历过内层for循环后，第二个4的下标为3，此时如果不进行i--的操作，就会少删去一个4。

2.双指针法<时间复杂度为O（n）的神奇方法>

双指针法的大体思路如下：首先定义一个快指针和一个慢指针，快指针从前向后遍历数组，当快指针指到的元素不为val时，快指针将该值赋值给慢指针，慢指针下标+1。
也就是说，慢指针指向的是要被赋值的下标，而快指针指向所要赋值的数字，举个例子，例如数组[1,2,3,3,4,5],val=3,整个过程如下：

fast=0 slow=0 a[slow]=1
fast=1 slow=1 a[slow]=2
fast=2 slow=1 a[slow]不赋值，因为a[fast]=val
fast=3 slow=1 a[slow]不赋值，因为a[fast]=val
fast=4 slow=2 a[slow]=4
fast=5 slow=3 a[slow]=5

源代码如下：

	int n=nums.size();
        int fast=0;
        int slow=0;
        for(fast=0;fast<n;fast++)
        {
           if(nums[fast]!=val)
           {
               nums[slow]=nums[fast];
               slow++;
           }
        }
        return slow;
        printf("%d, nums = [",n);
        for(int i=0;i<slow;i++)
        printf("%d,",nums[i]);
        printf("]");
    }