1. Toy模板网首页
  2. > Toy博客

算法篇——动态规划 完全和多重背包问题 (js版)

10月前 作者：低保和光头哪个先来 分类：Toy博客 阅读(45) 违法举报

这篇具有很好参考价值的文章主要介绍了算法篇——动态规划 完全和多重背包问题 (js版)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

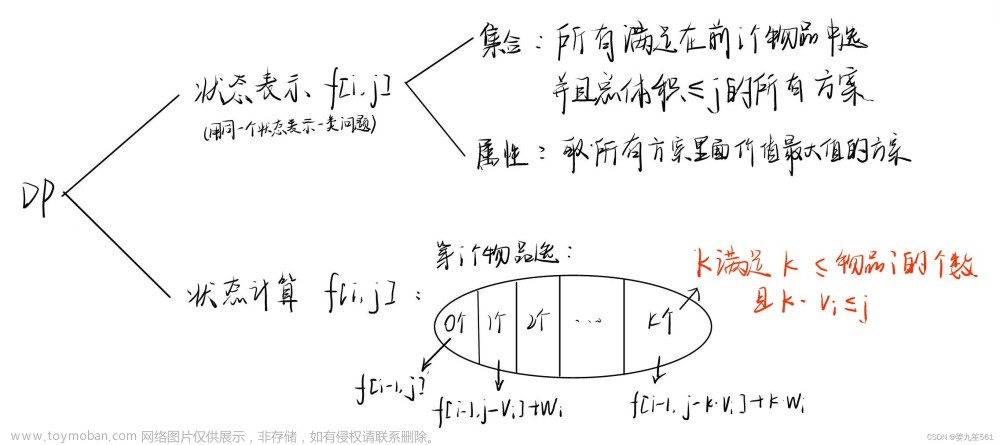
一些分析总结

01 背包 问题和 完全背包 问题的不同点在于，所有的物品只能使用一次，判断 哪些物品 装进背包里 物品价值和 最大；而 完全背包 问题中，所有物品都能使用n次，判断 哪个物品 装 n 个进去 物品价值和 最大。

01 背包的递推公式是：【当然先遍历物品还是背包的容量都可以】

for(var i = 0; i < nums.length; i++) {
   for(var j = target; j <= nums[i]; j++) {
      dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
   }
}

还有一种就是 一维滚动数组，原本的 二维数组 dp[i][j] 表示第 i 层、背包容量为 j 时的状态值，而递推中 只需要用到上一层的状态 dp[i-1][j] 和 dp[i-1][j-weight[i]]。因此，可以通过在一维数组中使用滚动的方式，将上一层的状态直接拷贝到当前层，从而节省空间。这种优化仅适用于无需回溯到更早层次，只需要关注前一层状态的情况。

for(var i = 0; i < nums.length; i++) {
    for(var j = target; j >= nums[i]; j--) {
        dp[j] = Math.max(dp[j], dp[j - nums[i]] + value[i]);
    }
}

这里的内层循环采用了倒序遍历，dp[j] 表示遍历到第 i 个物品、背包容量为 j 时的最优解。倒序遍历可以确保在计算 dp[j] 时，dp[j - weight[i]] 仍然表示第 i-1 个物品、背包容量为 j-weight[i] 时的最优解，不会受到当前层的状态更新影响。

接下来就是这篇文章的重头戏，完全背包 问题：每种物品都有无限件可供选择，求在有限的背包容量下，如何选择物品价值和最大化。

1.首先就是确立状态：dp[i][j] 表示前 i 个物品，背包容量为 j 时的最大价值。

对于第 i 个物品，可选放入多个此它，直到超过背包容量。 对于每个物品，要么放入，要么不放。

如果选择放入，剩余的背包容量就变成 j - weight[i]。 在放入一个物品后，变为求前 i 个物品，背包容量为 j - weight[i] 的最大价值，即 dp[i][j - weight[i]]。

如果选择不放入，变为求前 i-1 个物品，背包容量为 j 的最大价值，即 dp[i-1][j]。

因此递推公式为：

for(let j = 0; j <= bagWeight; j++) {
    for(let i = 0; i < nums.length; i++) {
        dp[j] = Math.max(dp[j], dp[j - nums[i]] + value[i])
    }
}

OR 

for(let i = 0; i < nums.length; i++) {
    for(let j = nums[i]; i <= bagWeight; j++) {
        dp[j] = Math.max(dp[j], dp[j - nums[i]] + value[i])
    }
}

此处的两层循环可以颠倒：

按照 外层循环是物品，内层循环是背包容量 的遍历方式时，如果当前物品 i 的重量 weight[i] 较小，在更新 dp[j] 的过程中，将会使用到同一层之前已经更新过的状态值 dp[j - weight[i]]。 由于 完全背包问题 每个物品可以选择多次，在计算 dp[j - weight[i]] 时，确保计算了当前物品 i ，得到 dp[j - weight[i] + value[i]]。在计算 dp[j] 时，如果再使用 dp[j - weight[i]] 进行更新，相当于将物品 i 又选一次，这样就允许了重复选择相同物品的情况。

进入正题 

518. 零钱兑换 II

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。 

题目数据保证结果符合 32 位带符号整数。

链接：力扣

javascript 背包问题,算法,动态规划,javascript

解题思路：

这道题是完全背包问题，但也涉及到排列组合的问题，因为 5=2+2+1 和 5=2+1+2 是两种组合方式，但我们这里只需要 组合方式 即可，上面说到完全背包问题的两层循环是可以颠倒的，但本题很特殊，如果进行了颠倒会怎么样，下面进行分析：

假如输入是 amount = 6, coins = [1, 5]

// 先遍历物品
for (let i = 0; i < coins.size(); i++) { 
    // 再遍历背包容量
    for (let j = coins[i]; j <= amount; j++) {
        dp[j] += dp[j - coins[i]]
    }
}

执行顺序：

  1. 外层循环遍历物品：

    • 从 i = 0 开始，遍历每个物品
    • coins.size() 表示物品的数量，coins[i] 表示第 i 个物品的价值

  2. 内层循环遍历背包容量：

    • 从 j = coins[i] 开始，直到超过目标容量 amount
    • dp[j] += dp[j - coins[i]] 表示更新当前背包容量 j 下的最优解，将之前计算过的状态值 dp[j - coins[i]] 加上当前物品的价值，即选择第 i 个物品的情况

通过依次遍历每个物品和背包容量，不断更新最优解，最终得到完全背包问题的最优解

先将 1 加入计算，再计算 5，得到的方法只有 {1, 5}，没有 {5, 1}，得到了组合数是 1

如果将两层循环进行颠倒：

// 先遍历背包容量
for (let j = 0; j <= amount; j++) {
    // 再遍历物品
    for (let i = 0; i < coins.length; i++) { 
        dp[j] += dp[j - coins[i]]
    }
}

执行顺序：

  1. 外层循环遍历背包容量，从0到金额 amount
  2. 内层循环遍历物品
  3. 在内循环中，对于每个背包容量 j，通过累加计算凑成金额 j 的组合数量
    • 逐个考虑当前物品的面额 coins[i]
    • 如果 j - coins[i] >= 0，表示可以选择当前物品，将其加入组合中
    • 更新状态转移方程 dp[j] += dp[j - coins[i]]，将前面计算得到的组合数量加到当前容量为 j 的组合数中
  4. 完成内层循环后，外层循环继续下一个背包容量的遍历
  5. 最终得到的数组 dp 中的元素 dp[amount] 即为凑成目标金额 amount 的组合数量

背包容量的每个值，都经过 1 和 5 ，包含了 {1, 5} 和 {5, 1} 两种情况，得到了排列数是 2

因此只能先遍历物品再遍历背包容量，完整代码如下：

var change = function(amount, coins) {
    // 如果这一个硬币等于 总金额，直接返回1
    if(coins.length == 1 && coins[0] == amount) return 1
    let dp = Array(amount + 1).fill(0)
    dp[0] = 1
    for(let i = 0; i < coins.length; i++) {
        for(let j = coins[i]; j <= amount; j++) {
            dp[j] += dp[j - coins[i]] 
        }
    }
    return dp[amount]
}
377. 组合总和 Ⅳ

给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。

题目数据保证答案符合 32 位整数范围。

链接：力扣

javascript 背包问题,算法,动态规划,javascript

解题思路：

本题就是区别于上题所说的，用到了排列的方式，以下是完整代码： 

var combinationSum4 = function(nums, target) {
    // 如果这一个元素等于 target ，直接返回1
    if(nums.length == 1) {
        if(nums[0] == target) return 1
        else if(nums[0] > target) return 0
    }
    let dp = Array(target + 1).fill(0)
    dp[0] = 1
    for(let j = 0; j <= target; j++) {
        for(let i = 0; i < nums.length; i++) {
            // 如果背包容量是大于当前元素的才能进行计算，不然装不下
            if(j >= nums[i]) dp[j] += dp[j - nums[i]] 
        }
    }
    return dp[target]
}

70. 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

链接：力扣

javascript 背包问题,算法,动态规划,javascript

var climbStairs = function(n) {
    const dp = [1, 2]
    for(let i = 2; i < n; ++i) {
        dp[i] = dp[i - 1] + dp[i - 2]
    }
    return dp[n-1]
}

322. 零钱兑换

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的
链接：力扣

javascript 背包问题,算法,动态规划,javascript

外层循环遍历每种硬币，内层循环从当前硬币的面值开始，到目标金额结束，逐个更新dp数组。对于每个金额j，将其更新为 dp[j-coins[i]] + 1 与原来的 dp[j] 之间的较小值，其中 coins[i] 表示当前硬币面值。

最后，函数返回 dp[amount] 的值，如果 dp[amount] 仍为无穷大，则说明无法凑成目标金额，返回-1；否则返回最少所需硬币数量。

var coinChange = function(coins, amount) {
    if(amount == 0) return 0
    if(coins.length == 1 && coins[0] > amount) return -1
    let dp = Array(amount + 1).fill(Infinity)
    dp[0] = 0
    for(let i =0; i < coins.length; i++) {
        for(let j = coins[i]; j <= amount; j++) {
            dp[j] = Math.min(dp[j - coins[i]] + 1, dp[j])
        }
    }
    return dp[amount] === Infinity ? -1 : dp[amount]
}

279. 完全平方数

给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。
链接：力扣

javascript 背包问题,算法,动态规划,javascript

  • 使用两层循环来遍历完全平方数。外层循环从1开始逐个取平方根，直到平方值 <= n
  • 内层循环从当前完全平方数开始，到目标数n结束，逐个更新dp数组。对于每个数j，将其更新为 dp[j-val] + 1 与原来的 dp[j] 之间的较小值，其中val表示当前完全平方数的值
var numSquares = function(n) {
    let dp = Array(n + 1).fill(Infinity)
    dp[0] = 0
    for(let i =1; i ** 2 <= n; i++) {
        let val = i ** 2
        for(let j = val; j <= n; j++) {
            dp[j] = Math.min(dp[j - val] + 1, dp[j])
        }
    }
    return dp[n]
}

139. 单词拆分

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。

注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。
链接：力扣

javascript 背包问题,算法,动态规划,javascript

var wordBreak = function(s, wordDict) {
    let dp = Array(s.length + 1).fill(false)
    dp[0] = true
    // 排列问题，先遍历背包容量，再遍历物品
    for(let i = 0; i <= s.length; i++){
        for(let j = 0; j < wordDict.length; j++) {
            if(i >= wordDict[j].length) {
                if(s.slice(i - wordDict[j].length, i) === wordDict[j] && dp[i - wordDict[j].length]) dp[i] = true
            }
        }
    }
    return dp[s.length]
}

198. 打家劫舍

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

链接：力扣

javascript 背包问题,算法,动态规划,javascript

解题思路：

“如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警”，则当我偷第 i  间房时，就不考虑 第 i-1 间，然后去偷 i+2 间房，反之就是偷 i-1 间房。 并且dp[0] 定是 nums[0]，dp[1] 是max(nums[0], nums[1])，来决定我以何种间隔进行计算。

var rob = function(nums) {
    if(nums.length == 0) return 0
    const dp = [nums[0], Math.max(nums[0], nums[1])]
    for(let i = 2; i < nums.length; i++) {
        // 错位相加
        dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i])
    }
    return dp[nums.length - 1]
}
213. 打家劫舍 II

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。

给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。
链接：力扣

javascript 背包问题,算法,动态规划,javascript

解题思路：

此题和上一题的不同之处就是成了环，在原有的相邻的不能偷的基础上，需要考虑情况偷了 nums[1] 就不能偷 nums[nums.length - 1]，这就是区别。

var rob = function(nums) {
    if(nums.length == 1) return nums[0]
    let res1 = toRob(nums, 0, nums.length - 2)
    let res2 = toRob(nums, 1, nums.length - 1)
    return Math.max(res1, res2)
}

var toRob = function(nums, start, end) {
    // 如果首尾相同，偷一个
    if(start == end) return nums[start]
    const dp = Array(nums.length).fill(0)
    // 从第一个开始
    dp[start] = nums[start]
    // 选择偷第一个房或第二个房
    dp[start+1] = Math.max(nums[start], nums[start+1])
    for(let i = start + 2; i <= end; i++) {
        dp[i] = Math.max(dp[i-2] + nums[i], dp[i-1])
    }
    return dp[end]
}

337. 打家劫舍 III

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。

除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。

给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额 。
链接：力扣

javascript 背包问题,算法,动态规划,javascript

javascript 背包问题,算法,动态规划,javascript解题思路：

通过使用一个长度为2的数组的状态转移方程，来记录状态变化，记录当前节点选择偷还是不偷所得到的最大金额，并且将其结果存储在哈希表中，避免了重复遍历。

需要分别计算不偷当前节点和偷当前节点的最大金额：

  • 不偷当前节点时，可以选择偷或不偷左子节点，偷或不偷右子节点，取两者之间最大值，保存在变量 Not 中
  • 偷当前节点时，不能偷其左右子节点，将当前节点的值 与 左子节点不偷的最大金额 与 右子节点不偷的最大金额 相加，保存在变量 Do 中
const rob = function(root) {
    // 通过哈希表保存已计算过的节点的结果
    const map = new Map()
    // 后序遍历函数
    const postOrderTraversal = function(node) {
        // 递归出口
        if (!node) return [0, 0]
        // 避免重复遍历
        if(map.has(node)) return map.get(node)
        // 遍历子树
        const left = postOrderTraversal(node.left)
        const right = postOrderTraversal(node.right)
        // 不偷当前节点，其左右子节点可以偷或不偷，取最大值
        const Not = Math.max(left[0], left[1]) + Math.max(right[0], right[1])
        // 偷当前节点，左右子节点只能不偷
        const Do = node.val + left[0] + right[0]
        // 返回选择偷还是不偷
        const result =  [Not, Do]
        map.set(node, result)
        return result
    }
    const res = postOrderTraversal(root)
    // 返回最大值
    return Math.max(...res)
}

121. 买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。
链接：力扣

javascript 背包问题,算法,动态规划,javascript

解题思路：

  1. dp[i] 表示第 i 天结束后的状态，每个状态由两个值组成：dp[i][0] 表示持有股票时的最大利润，dp[i][1] 表示不持有股票时的最大利润
  2. 初始化第一天的状态为 [-prices[0], 0]，即第一天选择买入股票，没有卖出
  3. 从第二天开始遍历价格数组，对于每一天 i：
    • dp[i][0] 的取值为 前一天持有股票的最大利润 与 当天买入股票后的利润 中的较大值，即 Math.max(dp[i - 1][0], -prices[i])。表示选择 保持前一天的股票状态 或 将前一天 不持有股票 的状态转变为 持有股票 的状态
    • dp[i][1] 的取值为 前一天不持有股票的最大利润 与 当天卖出股票后的利润 中的较大值，即 Math.max(dp[i - 1][1], prices[i] + dp[i - 1][0])。表示选择 保持前一天的股票状态 或 将前一天持有股票 的状态转变为 不持有股票 的状态，并获得当天的卖出利润
  4. 最终结果为 dp[len - 1][1]，表示最后一天不持有股票时的最大利润

贪心算法： 

var maxProfit = function(prices) {
    if(prices.length == 1) return 0
    let min = prices[0], max = 0
    for(let i = 0; i < prices.length; i++) {
        // 前一天的差值和今天卖出的差值
        max = Math.max(max, prices[i] - min)
        // 之前买入的价格和今天买入的价格
        min = Math.min(min, prices[i])
    }
    return max
}

动态规划：

var maxProfit = function(prices) {
    const len = prices.length
    // 创建dp数组
    const dp = new Array(len).fill([0, 0])
    // dp 数组初始化
    dp[0] = [-prices[0], 0]
    for (let i = 1; i < len; i++) {
        // 更新dp[i]
        dp[i] = [
            // 前一天持有股票的最大利润 与 当天买入股票后的利润 的最大值
            Math.max(dp[i - 1][0], -prices[i]),
            // 前一天不持有股票的最大利润 与 当天卖出股票后的利润 的最大值
            Math.max(dp[i - 1][1], prices[i] + dp[i - 1][0]),
        ]
    }
    return dp[len - 1][1]
}

122. 买卖股票的最佳时机 II

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。
链接：力扣

javascript 背包问题,算法,动态规划,javascript

本题和上一题的不同之处在于：

  • 上一题股票只能买卖一次，如果买入股票，那么第 i 天持有股票，即 dp[i][0] 是 -prices[i]
  • 本题一只股票可以买卖多次，当第 i 天买入股票时，持有的现金可能有之前产生的利润
  • 第 i 天持有股票即 dp[i][0]，如果第 i 天买入股票，所得现金是 昨天不持有股票的所得现金 减去 今天的股票价格，即 dp[i - 1][1] - prices[i]

贪心算法： 

var maxProfit = function(prices) {
    var res = 0
    // 计算正利润
    var odd = 0
    for(var i = prices.length-1; i >= 0; i--) {
        // 进行差值计算
        odd = prices[i] - prices[i-1]
        // 如果是正利润就放入结果中
        if(odd > 0) res += odd
        else odd = 0
    }
    return res
}

动态规划：

var maxProfit = function(prices) {
    const len = prices.length
    let dp = Array.from(Array(len).fill(0))
    dp[0] = [-prices[0], 0]
    for(let i = 1; i < len; i++) {
        dp[i] = [
            // dp[i-1][1] - prices[i] = 不持有的利润 减去 买入的价格
            Math.max(dp[i-1][0], dp[i-1][1] - prices[i]),
            Math.max(dp[i-1][1], dp[i-1][0] + prices[i])
        ]
    }
    return dp[len -1][1]
}
123. 买卖股票的最佳时机 III

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
链接：力扣

javascript 背包问题,算法,动态规划,javascript

解题思路：

这一题相较于上面两题，不同之处在于，只能进行两次交易，因此我们需要考虑：

何时第一次买入，何时第一次卖出

何时第二次买入，何时第二次卖出

代码不同的地方就是递推公式需要判断 买入时的利润 和 卖出的利润 是基于第几次 

var maxProfit = function(prices) {
    const len = prices.length
    let dp = Array.from(Array(len).fill(0))
    dp[0] = [-prices[0], 0, -prices[0], 0]
    for(let i = 1; i < len; i++) {
        dp[i] = [
            Math.max(dp[i-1][0], -prices[i]),
            Math.max(dp[i-1][1], dp[i-1][0] + prices[i]),
            Math.max(dp[i-1][2], dp[i-1][1] - prices[i]),
            Math.max(dp[i-1][3], dp[i-1][2] + prices[i])
        ]
    }
    return dp[len -1][3]
}
188. 买卖股票的最佳时机 IV

给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格，和一个整型 k 。设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说，你最多可以买 k 次，卖 k 次。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
链接：力扣

javascript 背包问题,算法,动态规划,javascript

解题思路：

基于上面一题的思路，我们不可能将k次全部列出，但卖出之前必须买入，可得，奇数时买入，偶数时卖出

  • 初始化第一天的状态，对于奇数索引 j，即买入状态，将其设置为 0 - prices[0]，表示第一天进行买入操作得到的利润
  • 从第二天开始遍历价格数组，对于每一天 i 和交易次数索引 j（从0开始，以2递增）
  • 更新 dp[i][j+1]，表示第 i 天结束后进行 j+1 次交易时 持有股票的最大利润。取 前一天持有股票的最大利润 dp[i-1][j+1] 和 前一天不持有股票的最大利润 加 当天买入股票后的利润 的较大值
var maxProfit = function(k, prices) {
    const len = prices.length
    // 行数 prices.length，列数 2 * k + 1
    let dp = Array.from(Array(prices.length), () => Array(2*k+1).fill(0))
    // 第一天买入时得到的利润
    for(let i = 1; i < 2 * k; i += 2) {
        dp[0][i] = -prices[0]
    }
    for(let i = 1; i < len; i++) {
        for (let j = 0; j < 2 * k; j += 2) {
            dp[i][j+1] = Math.max(dp[i-1][j+1], dp[i-1][j] - prices[i]);
            dp[i][j+2] = Math.max(dp[i-1][j+2], dp[i-1][j+1] + prices[i]);
        }
    }
    return dp[len - 1][2 * k]
}
309. 最佳买卖股票时机含冷冻期

给定一个整数数组prices，其中第  prices[i] 表示第 i 天的股票价格 。​

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
链接：力扣

 javascript 背包问题,算法,动态规划,javascript

dp[i][0]：表示第 i 天结束时持有股票的最大利润

dp[i][1]：表示第 i 天结束时不持有股票且处于冷冻期的最大利润

dp[i][2]：表示第 i 天结束时不持有股票且不处于冷冻期的最大利润

var maxProfit = function(prices) {
    const len = prices.length
    let dp = Array.from(Array(len), () => Array(3).fill(0))
    dp[0][0] = -prices[0]
    for (let i = 1; i < len; i++) {
        dp[i][0] = Math.max(dp[i - 1][2] - prices[i], dp[i - 1][0])
        dp[i][1] = dp[i - 1][0] + prices[i]
        dp[i][2] = Math.max(dp[i - 1][1], dp[i - 1][2])
    }
    return Math.max(dp[len - 1][1], dp[len - 1][2])
}

714. 买卖股票的最佳时机含手续费

给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格 ；整数 fee 代表了交易股票的手续费用。

你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。
链接：力扣

javascript 背包问题,算法,动态规划,javascript文章来源地址https://www.toymoban.com/news/detail-712418.html

var maxProfit = function(prices, fee) {
    const len = prices.length
    let dp = Array.from(Array(len).fill(0))
    dp[0] = [-prices[0], 0]
    for(let i = 1; i < len; i++) {
        dp[i] = [
            Math.max(dp[i-1][0], dp[i-1][1] - prices[i]),
            Math.max(dp[i-1][1], dp[i-1][0] + prices[i] - fee)
        ]
    }
    return dp[len -1][1]
}

到了这里，关于算法篇——动态规划 完全和多重背包问题 (js版)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • 【算法日志】动态规划刷题：01背包问题，多重背包问题(day37,day38)

    【算法日志】动态规划刷题：01背包问题，多重背包问题(day37,day38)

    目录 前言 目标和（01背包） 一和零（01背包） 零钱兑换（多重背包） 排列总和（多重背包） 这两天都是背包问题，其中的01背包的一些应用问题需要一定的数学建模能力，需要i将实际问题简化成我们熟悉的背包问题；而这两天的多重背包问题还算比较基础，但也要我明白了

    2024年02月11日
    浏览(56)
  • 算法系列--动态规划--背包问题(3)--完全背包介绍

    算法系列--动态规划--背包问题(3)--完全背包介绍

    💕\\\"Su7\\\"💕 作者：Lvzi 文章主要内容：算法系列–动态规划–背包问题(3)–完全背包介绍 大家好,今天为大家带来的是 算法系列--动态规划--背包问题(3)--完全背包介绍 链接: 完全背包 可以发现完全背包问题和01背包问题还是特比相似的 分析: 完全背包问题 是 01背包问题 的推广

    2024年04月25日
    浏览(44)
  • 力扣刷题-动态规划算法3：完全背包问题

    力扣刷题-动态规划算法3：完全背包问题

    问题描述： 1）有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。 2） 每件物品都有无限个（也就是可以放入背包多次） （比0-1背包多出的条件） 3） 求解将哪些物品装入背包里物品价值总和最大。 求解步骤： 1）首先遍历物品，然

    2023年04月13日
    浏览(58)
  • 动态规划：完全背包问题----中专生刷算法

    动态规划：完全背包问题----中专生刷算法

    需要基础:闫氏dp分析法，01背包问题 先去看一下01背包问题，再看完全背包 动态规划:选择dp及优化01背包问题-CSDN博客 做过01背包问题的同学会发现,完全背包问题的代码 在01背包基础上改动很小，但是里面的思想，有很大差距 题目 有 N 种物品和一个容量是 V的背包，每种物品

    2024年04月16日
    浏览(47)
  • 算法套路十四——动态规划之背包问题：01背包、完全背包及各种变形

    算法套路十四——动态规划之背包问题：01背包、完全背包及各种变形

    如果对递归、记忆化搜索及动态规划的概念与关系不太理解，可以前往阅读算法套路十三——动态规划DP入门 背包DP介绍：https://oi-wiki.org/dp/knapsack/ 0-1背包:有n个物品，第i个物品的体积为w[i]，价值为v[i]，每个物品至多选一个， 求体积和不超过capacity时的最大价值和，其中i从

    2024年02月10日
    浏览(59)
  • 动态规划DP之背包问题3---多重背包问题

    动态规划DP之背包问题3---多重背包问题

    目录 DP分析： 优化：  二进制优化 例题：         01背包是每个物品只有一个，完全背包问题是每个物品有无限个。         那么多重背包问题就是 每个物品有有限个 。 有 N 种物品和一个容量是 V 的背包。 第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。 求解

    2024年03月20日
    浏览(49)

  • 力扣算法刷题Day44｜动态规划：完全背包问题 零钱兑换II 组合总和Ⅳ

    力扣题目：#518.零钱兑换II（完全背包组合问题） 刷题时长：7min 解题方法：动态规划（完全背包） 复杂度分析 时间复杂度: O(mn)，其中 m 是amount，n 是 coins 的长度 空间复杂度: O(m) 问题总结 对递推公式的理解 本题收获 题意转换：纯完全背包是凑成背包最大价值是多少，而本

    2024年02月13日
    浏览(41)

  • 动态规划-背包问题-完全背包

    对比01背包，完全背包中的每件物品有无数件。 也就是说，每件物品可以拿0，1，…，k，…件。 dp[i][j]表示前i种物品，体积为j时的最大价值 对于第i件物品： 不拿：dp[i][j]⇐dp[i-1][j] 拿一件：dp[i][j]⇐dp[i-1][j-w[i]]+v[i] 拿两件：dp[i][j]⇐dp[i-1][j-2w[i]]+2v[i] … 拿k件：dp[i]][j]⇐dp[i

    2024年04月08日
    浏览(49)

  • 动态规划之背包问题——完全背包

    算法相关数据结构总结： 序号 数据结构 文章 1 动态规划 动态规划之背包问题——01背包 动态规划之背包问题——完全背包 动态规划之打家劫舍系列问题 动态规划之股票买卖系列问题 动态规划之子序列问题 算法（Java）——动态规划 2 数组 算法分析之数组问题 3 链表 算法

    2024年02月03日
    浏览(63)
  • 算法竞赛必考算法——动态规划(01背包和完全背包）

    算法竞赛必考算法——动态规划(01背包和完全背包）

    1.1题目介绍 1.2思路一介绍(二维数组) 代码如下： 1.3思路二介绍(一维数组) 空间优化   为什么可以使用一维数组？   我们先来看一看01背包问题的状态转移方程，我们可以发现 f[i]只用到了f[i-1]，其他的是没有用到的，我们可以用滚动数组来做。   还有一个原因就是我

    2024年02月02日
    浏览(42)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包