广度搜索与深度搜索的区别-Toy模板网

这篇具有很好参考价值的文章主要介绍了广度搜索与深度搜索的区别。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

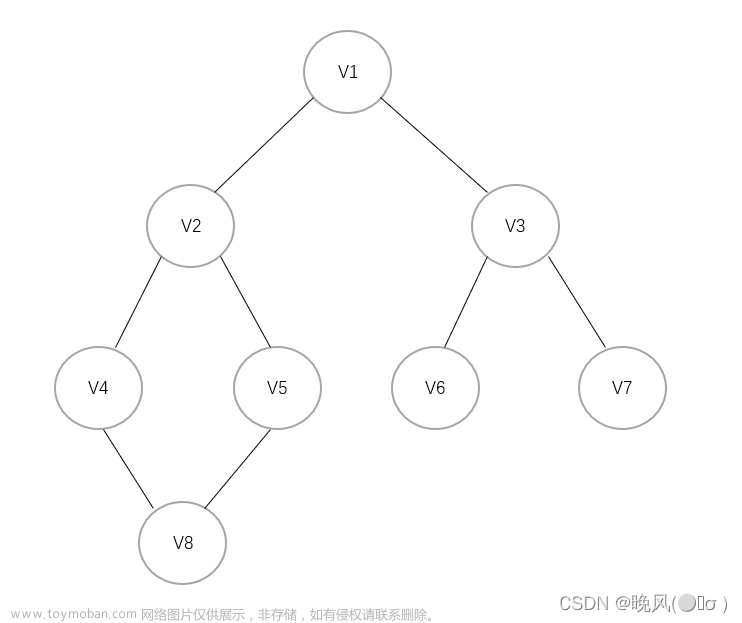
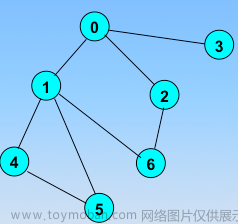
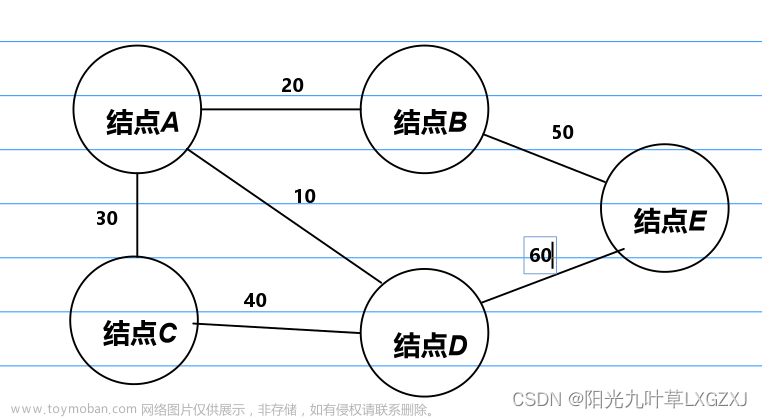
广度搜索（Breadth-First Search，BFS）是一种基于图的遍历算法，它按照广度优先的方式遍历图中的所有节点。具体来说，该算法从起点开始向外扩展，先遍历起点所有直接相邻的节点，然后再遍历这些节点的直接相邻节点，以此类推。BFS算法可以用于寻找两点之间的最短路径，也可以用于检查图的连通性、拓扑排序等问题。以下是广度搜索算法的基本实现步骤：

创建一个空队列，将起点入队。

标记起点为已访问。

当队列不为空时，重复以下步骤：

从队列中取出一个节点，访问它之后将其出队。

遍历该节点的所有邻居节点，如果邻居节点未被访问过，则将其标记为已访问，并将其入队。

如果所有节点都被访问过，则算法结束；否则，返回第一步。

需要注意的是，由于广度搜索需要遍历相邻的所有节点，因此它通常需要使用额外的开销来存储每个节点的邻居信息。对于大型图来说，该算法的内存消耗可能会很大，因此需要进行优化。同时，BFS算法的时间复杂度为O(|V|+|E|)，其中|V|表示节点数量，|E|表示边的数量。因此，对于密集图来说，该算法的时间复杂度会很高。

深度搜索（Depth-First Search，DFS）是一种基于图的遍历算法，它沿着一条路径尽可能深地访问每个节点，直到不能再继续下去为止，然后返回上一级节点，继续深度优先遍历其他路径。DFS算法可以用于寻找图中的所有连通块、找到两点之间的路径、拓扑排序、解决迷宫等问题。以下是DFS算法的基本实现步骤：

标记起点为已访问，并将其加入路径。

对于当前节点的每个未访问的相邻节点，重复以下步骤：

标记相邻节点为已访问。

将相邻节点加入路径。

递归访问相邻节点（即重复步骤2）。

如果所有相邻节点都已经访问过，将当前节点从路径中删除。

如果所有节点都被访问过，则算法结束；否则，重复步骤1。

需要注意的是，DFS算法可能会陷入死循环或超出递归深度限制。通常情况下，使用迭代模拟递归或剪枝等技巧可以避免这些问题。此外，DFS算法并没有保证能够找到最短路径。如果需要找到两点之间的最短路径，可以考虑使用广度搜索（BFS）算法。

广度搜索和深度搜索的使用场景略有不同，下面分别介绍：

广度搜索的使用场景
最短路径查询：在无权图中，广度搜索可以找到两个节点之间的最短路径。这是因为在广度搜索中，每个节点都是从与它距离为1的节点扩展而来。所以第一次到达目的节点时，路径长度一定最短。

连通性检查：广度搜索可以检查无向图或有向图中的节点是否连接。如果一个图是连通的，那么在广度搜索中可以从任何一个节点到达所有其他节点。

拓扑排序：广度搜索可以对有向无环图(DAG)进行拓扑排序。

状态转移问题：广度搜索可以处理状态转移问题，如八数码、华容道等。

深度搜索的使用场景
有限状态机：若一个系统必须经历一系列状态才能达成目标，就可以采用DFS来解决问题。

生成全部排序：可以使用深度搜索来生成一个序列的全排列。

能力匹配问题：比如，确定一个人的技能是否能够完成一项任务。

子集和问题：给定一个集合和一个目标值，求出集合中的子集和是否能够等于该目标值。

综上所述，广度搜索和深度搜索在使用场景上有所差异。如果需要找到两个节点之间的最短路径、检查节点之间的连通性、进行拓扑排序等问题，可以使用广度搜索。如果需要处理能力匹配问题、生成全部排序、解决子集和问题等，可以使用深度搜索。

以下是广度搜索的 Python 实现，其中假设图用邻接表的形式给出：

from collections import deque

def bfs(graph, start):
visited = set() # 用集合记录已访问的节点
queue = deque([start]) # 用双端队列存储待访问的节点

while queue:
    node = queue.popleft()  # 取出队列首部的节点
    visited.add(node)
    print(node)

    for neighbor in graph[node]:  # 遍历相邻节点
        if neighbor not in visited:  # 如果相邻节点未被访问过，则将其标记为已访问并加入队列尾部
            visited.add(neighbor)
            queue.append(neighbor)

注意，上述代码只是对图进行遍历，并没有实现寻找最短路径等具体操作。如果需要根据广度搜索找到最短路径，可以在记录已访问节点的同时，额外记录每个节点的前驱节点，最后沿着前驱节点回溯即可。

以下是深度搜索的 Python 实现，其中假设图用邻接表的形式给出：

def dfs(graph, node, visited=None):
if visited is None: # 对访问过的节点进行标记
visited = set()
visited.add(node)
print(node)

for neighbor in graph[node]:
    if neighbor not in visited:  # 如果相邻节点未被访问过，则递归地访问它
        dfs(graph, neighbor, visited)

注意，递归过程中需要对已访问的节点进行标记，避免重复访问。如果需要根据深度搜索找到特定两节点之间的路径，可以在访问节点时记录路径，最后回溯即可。同时，需要注意循环调用的递归深度，可能会超出递归深度限制，需要做好异常处理。文章来源地址https://www.toymoban.com/news/detail-712619.html

到了这里，关于广度搜索与深度搜索的区别的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！