一、最长公共子序列
若给定序列X={x1,x2,…,xm},则另一序列Z={z1,z2,…,zk},是X的 子序列 是指存在一个严格递增下标序列{i1,i2,…,ik}使得对于所有j=1,2,…,k有:zj=xij。例如,序列Z={B,C,D,B}是序列X={A,B,C,B,D,A,B}的子序列,相应的递增下标序列为{2,3,5,7}。
给定2个序列X和Y,当另一序列Z既是X的子序列又是Y的子序列时,称Z是序列X和Y的公共子序列。
给定2个序列X={x1,x2,…,xm}和Y={y1,y2,…,yn},找出X和Y的 最长公共子序列。
1.1 最长公共子序列的结构
设序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}的最长公共子序列为Z={z1,z2,…,zk} ,则
(1)若xm=yn,则zk=xm=yn,且zk-1是xm-1和yn-1的最长公共子序列。
(2)若xm≠yn且zk≠xm,则 Z是xm-1和Y的最长公共子序列。
(3)若xm≠yn且zk≠yn,则 Z是X和yn-1的最长公共子序列。
由此可见,2个序列的最长公共子序列包含了这2个序列的前缀的最长公共子序列。因此,最长公共子序列问题具有最优子结构性质。
1.2 子问题的递归结构
由最长公共子序列问题的最优子结构性质建立子问题最优值的递归关系。用c[i][j]记录序列和的最长公共子序列的长度。其中, Xi={x1,x2,…,xi};Yj={y1,y2,…,yj}。当i=0或j=0时,空序列是Xi和Yj的最长公共子序列。故此时C[i][j]=0。其它情况下,由最优子结构性质可建立递归关系如下:
1.3 计算最优值
由于在所考虑的子问题空间中,总共有θ(mn)个不同的子问题,因此,用动态规划算法自底向上地计算最优值能提高算法的效率。
void LCSLength(int m,int n,char *x,char *y,int **c,int **b)
{
int i,j;
for (i = 1; i <= m; i++) c[i][0] = 0;
for (i = 1; i <= n; i++) c[0][i] = 0;
for (i = 1; i <= m; i++)
for (j = 1; j <= n; j++) {
if (x[i]==y[j]) {
c[i][j]=c[i-1][j-1]+1; b[i][j]=1;}
else if (c[i-1][j]>=c[i][j-1]) {
c[i][j]=c[i-1][j]; b[i][j]=2;}
else { c[i][j]=c[i][j-1]; b[i][j]=3; }
}
}
//构造最长公共子序列
void LCS(int i,int j,char *x,int **b)
{
if (i ==0 || j==0) return;
if (b[i][j]== 1){ LCS(i-1,j-1,x,b); cout<<x[i]; }
else if (b[i][j]== 2) LCS(i-1,j,x,b);
else LCS(i,j-1,x,b);
}
1.4 举例说明

1.5 算法的改进
在算法lcsLength和lcs中,可进一步将数组b省去。事实上,数组元素c[i][j]的值仅由c[i-1][j-1],c[i-1][j]和c[i][j-1]这3个数组元素的值所确定。对于给定的数组元素c[i][j],可以不借助于数组b而仅借助于c本身在时间内确定c[i][j]的值是由c[i-1][j-1],c[i-1][j]和c[i][j-1]中哪一个值所确定的。
如果只需要计算最长公共子序列的长度,则算法的空间需求可大大减少。
事实上,在计算c[i][j]时,只用到数组c的第i行和第i-1行。因此,用2行的数组空间就可以计算出最长公共子序列的长度。进一步的分析还可将空间需求减至O(min(m,n))。
二、最大子段和
子段:数列中的连续若干子数列的集合
问题:给定由n个整数(可能为负整数)组成的序列a1,a2,…an,求该序列的子段和的最大值
当所有整数均为负整数时,定义其最大子段和为零
例如,当(a1,a2,a3,a4,a5,a6)=(-2,11,-4,13,-5,-2)时,最大子段和为20。
2.1 代码
int MaxSum(int n,int *a){
int besti,bestj;
int i,j,k,thissum;
int sum=0;
for(i=1;i<=n;i++){
for(j=i;j<=n;j++){
thissum=0;
for(k=i;k<=j;k++)
thissum+=a[k];
if (thissum>sum){
sum=thissum;
besti=i;
bestj=j;
}
}
}
return sum;
}
2.2 最大子段和问题的分治算法
将所给的序列a[1:n],分成长度相等的两端a[1:n/2]和 a[n/2+1:n],分别求出这两端的最大子段和,则 a[1:n]的最大子段和有三种情况:
a[1:n]的最大子段和与a[1:n/2]的最大子段和相同;
a[1:n]的最大子段和与a[n/2+1:n]的最大子段和相同;
a[1:n]的最大子段和跨越a[1:n/2]和a[n/2+1:n]两个区域。
对于3,容易看出,a[n/2]与a[n/2+1]必在最优子序列中!
在a[1:n/2]中计算出s1为含有a[n/2]的最大子段和。
在a[n/2+1:n]中计算出s2为含有a[n/2+1]的最大子段和。
则s1+s2即为出现情形3时的最优值。
int MaxSubSum(int *a,int left,int right){
int sum=0;
int center;
int leftsum,rightsum;
int i,s1,s2,lefts,rights;
if(left==right)
sum=a[left]>0?a[left]:0;
else{
center=(left+right)/2;
leftsum=MaxSubSum(a,left,center);
rightsum=MaxSubSum(a,center+1,right);
s1=0;
lefts=0;
for(i=center;i>=left;i--){
lefts+=a[i];
if(lefts>s1)
s1=lefts;
}
s2=0;
rights=0;
for(i=center+1;i<=right;i++){
rights+=a[i];
if(rights>s2)
s2=rights;
}
2.3 代码
sum=s1+s2;
if(sum<leftsum)
sum=leftsum;
if(sum<rightsum)
sum=rightsum;
}
return sum;
}
2.4 分治算法的时间复杂度
该算法所需的计算时间T(n)满足典型的分治算法递归式。
解此递归方程可知,T(n)= O(nlogn)。
2.5 最大子段和问题的动态规划算法
若记b[j]为必须包含a[j]的左侧连续数据的最大子段和,则所求的最大子段和为max(1到n) b[j],再用变量sum存储当前b[j]的最大值即可。
由于程序只用了一个for循环,所以此算法的时间复杂度为O(n)。
由b[j]的定义易知:
当b[j-1]>0 时,b[j]= b[j-1]+a[j],否则b[j]= a[j]。由此可得b[j]的动态规划递归式b[j]= max{b[j-1]+a[j],a[j]},1<=j<=n。
据此,可以设计出求最大字段和的动态规划算法。
代码如下:
int MaxSum(int n,int *a){
int i,sum=0,b=0;
for(i=1;i<=n;i++){
if(b>0)
b+=a[i];
else
b=a[i];
if(b>sum)
sum=b;
}
return sum;
}
三、凸多边形最优三角剖分
用多边形顶点的逆时针序列表示凸多边形,即P={v0,v1,…,vn-1}表示具有n条边的凸多边形。
若vi与vj是多边形上不相邻的2个顶点,则线段vivj称为多边形的一条弦。弦将多边形分割成2个多边形{vi,vi+1,…,vj}和{vj,vj+1,…vi}。
多边形的三角剖分是将多边形分割成互不相交的三角形的弦的集合T。
给定凸多边形P,以及定义在由多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分,使得即该三角剖分中诸三角形上权之和为最小。
3.1 三角剖分的结构及其相关问题
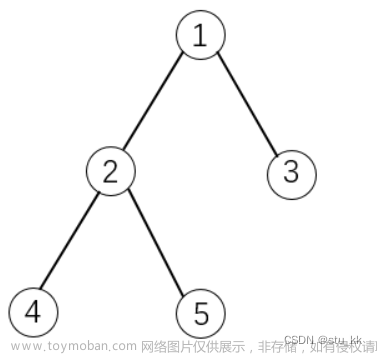
一个表达式的完全加括号方式相应于一棵完全二叉树,称为表达式的语法树。例如,完全加括号的矩阵连乘积((A1(A2A3))(A4(A5A6)))所相应的语法树如图 (a)所示。
凸多边形{v0,v1,…vn-1}的三角剖分也可以用语法树表示。例如,图 (b)中凸多边形的三角剖分可用图 (a)所示的语法树表示。
矩阵连乘积中的每个矩阵Ai对应于凸(n+1)边形中的一条边vi-1vi。三角剖分中的一条弦vivj,i<j,对应于矩阵连乘积A[i+1:j]。
3.2 最优子结构性质
凸多边形的最优三角剖分问题有最优子结构性质。
事实上,若凸(n+1)边形P={v0,v1,…,vn-1}的最优三角剖分T包含三角形v0vkvn,1≤k≤n-1,则T的权为3个部分权的和:三角形v0vkvn的权,子多边形{v0,v1,…,vk}和{vk,vk+1,…,vn}的权之和。
可以断言,由T所确定的这2个子多边形的三角剖分也是最优的。因为若有{v0,v1,…,vk}或{vk,vk+1,…,vn}的更小权的三角剖分将导致T不是最优三角剖分的矛盾。
3.3 最优三角剖分的递归结构
定义t[i][j],1≤i<j≤n为凸子多边形{vi-1,vi,…,vj}的最优三角剖分所对应的权函数值,即其最优值。为方便起见,设退化的多边形{vi-1,vi}具有权值0。据此定义,要计算的凸(n+1)边形P的最优权值为t[1][n]。
t[i][j]的值可以利用最优子结构性质递归地计算。当j-i≥1时,凸子多边形至少有3个顶点。由最优子结构性质,t[i][j]的值应为t[i][k]的值加上t[k+1][j]的值,再加上三角形vi-1vkvj的权值,其中i≤k≤j-1。由于在计算时还不知道k的确切位置,而k的所有可能位置只有j-i个,因此可以在这j-i个位置中选出使t[i][j]值达到最小的位置。由此,t[i][j]可递归地定义为:
四、图像压缩
图象的变位压缩存储格式将所给的象素点序列{p1,p2,…,pn},0≤pi≤255分割成m个连续段S1,S2,…,Sm。第i个象素段Si中(1≤i≤m),有l[i]个象素,且该段中每个象素都只用b[i]位表示。
设
则第i个象素段Si为
设 ,则hib[i]8。因此需要用3位表示b[i],如果限制1l[i]255,则需要用8位表示l[i]。因此,第i个象素段所需的存储空间为l[i]*b[i]+11位。按此格式存储象素序列{p1,p2,…,pn},需要
,则hib[i]8。因此需要用3位表示b[i],如果限制1l[i]255,则需要用8位表示l[i]。因此,第i个象素段所需的存储空间为l[i]*b[i]+11位。按此格式存储象素序列{p1,p2,…,pn},需要 位的存储空间。
位的存储空间。
图象压缩问题要求确定象素序列{p1,p2,…,pn}的最优分段,使得依此分段所需的存储空间最少。每个分段的长度不超过256位。
设l[i],b[i],是{p1,p2,…,pn}的最优分段。显而易见,l[1],b[1]是{p1,…,pl[1]}的最优分段,且l[i],b[i],是{pl[1]+1,…,pn}的最优分段。即图象压缩问题满足最优子结构性质。
设s[i],1≤i≤n,是象素序列{p1,…,pn}的最优分段所需的存储位数。由最优子结构性质易知:
其中,
算法复杂度分析:
由于算法compress中对k的循环次数不超这256,故对每一个确定的i,可在时间O(1)内完成的计算。因此 整个算法所需的计算时间为O(n)。
五、电路布线
在一块电路板的上、下2端分别有n个接线柱。根据电路设计,要求用导线(i,π(i))将上端接线柱与下端接线柱相连,如图所示。其中π(i)是{1,2,…,n}的一个排列。导线(i,π(i))称为该电路板上的第i条连线。对于任何1≤i<j≤n,第i条连线和第j条连线相交的充分且必要的条件是π(i)>π(j)。
电路布线问题要确定将哪些连线安排在第一层上,使得该层上有尽可能多的连线。换句话说,该问题要求确定导线集Nets={(i,π(i)),1≤i≤n}的最大不相交子集。
记
N(i,j)的最大不相交子集为MNS(i,j)。Size(i,j)=|MNS(i,j)|。
(1)当i=1时,
(2)当i>1时,
若j<π(i)。此时,
故在这种情况下,N(i,j)=N(i-1,j),从而Size(i,j)=Size(i-1,j)。
2.2 j≥π(i),(i,π(i))∈MNS(i,j) 。 则对任意(t,π(t)) ∈MNS(i,j)有t<i且π(t)<π(i)。在这种情况下MNS(i,j)-{(i,π(i))}是N(i-1,π(i)-1)的最大不相交子集。
若
则对任意(t,π(t)) ∈MNS(i,j)有t<i。从而
因此,Size(i,j)≤Size(i-1,j)。
另一方面,
故又有Size(i,j)≥Size(i-1,j),从而Size(i,j)=Size(i-1,j)。
5.1 代码
void MNS(int C[],int n){
int i,j;
for(j=0;j<C[1];j++){
size[1][j]=0;
}
for(j=C[1];j<=n;j++){
size[1][j]=1;
}
for(i=2;i<n;i++){
for(j=0;j<C[i];j++){
size[i][j]=size[i-1][j];
}
for(j=C[i];j<=n;j++){
size[i][j]=size[i-1][j]>(size[i-1][C[i]-1]+1)?size[i-1][j]:(size[i-1][C[i]-1]+1);
}
}
size[n][n]=size[n-1][n]>(size[n-1][C[n]-1]+1)?size[n-1][n]:(size[n-1][C[n]-1]+1);
}
void Traceback(int C[],int n,int NET[]){
int i,j=n;
int m=0;
for(i=n;i>1;i--){
if(size[i][j]!=size[i-1][j]){
NET[m++]=i;
j=C[i]-1;
}
if(j>=C[1])
NET[m++]=1;
}
}
六、流水作业调度
n个作业{1,2,…,n}要在由2台机器M1和M2组成的流水线上完成加工。每个作业加工的顺序都是先在M1上加工,然后在M2上加工。M1和M2加工作业i所需的时间分别为ai和bi。
流水作业调度问题要求确定这n个作业的最优加工顺序,使得从第一个作业在机器M1上开始加工,到最后一个作业在机器M2上加工完成所需的时间最少。
分析:
直观上,一个最优调度应使机器M1没有空闲时间,且机器M2的空闲时间最少。在一般情况下,机器M2上会有机器空闲和作业积压2种情况。
设全部作业的集合为N={1,2,…,n}。S⊆N是N的作业子集。在一般情况下,机器M1开始加工S中作业时,机器M2还在加工其它作业,要等时间t后才可利用。将这种情况下完成S中作业所需的最短时间记为T(S,t)。流水作业调度问题的最优值为T(N,0)。
设π是所给n个流水作业的一个最优调度,它所需的加工时间为 aπ(1)+T’。其中T’是在机器M2的等待时间为bπ(1)时,安排作业π(2),…,π(n)所需的时间。
记S=N-{π(1)},则有T’=T(S,bπ(1))。
证明:事实上,由T的定义知T’≤T(S,bπ(1))。若T’>T(S,bπ(1)),设π’是作业集S在机器M2的等待时间为bπ(1)情况下的一个最优调度。则π(1), π’(2),…, π’(n)是N的一个调度,且该调度所需的时间为aπ(1)+T(S,bπ(1))<aπ(1)+T’。这与π是N的最优调度矛盾。故T’≤T(S,bπ(1))。从而T’=T(S,bπ(1))。这就证明了流水作业调度问题具有最优子结构的性质。
由 流水作业调度问题的最优子结构性质 可知,

七、投资问题
问题:m元钱,n项投资,fi(x):将x元投入第i个项目的效益。求使得总效益最大的投资方案。
建模:问题的解是向量<x1,x2,…xn>,xi是投给项目i的钱数,i=1,2,…,n
目标函数max{f1(x1)+f2(x2)+…+fn(xn)}。
约束条件x1+x2+…+xn=m,xi∈N。
7.1 实例
5万元钱,4个项目,效益函数如下表所示
7.2 子问题界定和计算顺序
子问题界定:由参数k和x界定。
k:考虑对项目1,2,…,k的投资
x:投资总钱数不超过x
原始输入:k=n,x=m
子问题计算顺序:
k=1,2,…,n
对于给定的k,x=1,2,…,m
7.3 优化函数的递推方程
Fk(x):x元钱投给前k个项目的最大效益。
多步判断:若知道p元钱(p<=x)投给前k-1个项目的最大效益Fk-1§,确定x元钱投给前k个项目的方案。
递推方程和边界条件:
Fk(x)=max{fk(xk)+Fk-1(x-xk)} k>1。
F1(x)=f1(x)。
7.5 k=1时实例的计算
F1(1)=11。
F1(2)=12。
F1(3)=13。
F1(4)=14。
F1(5)=15。
7.6 k=2时的实例计算
方案(其它,项目2):(0,1),(1,0)
F2(1)=max{f2(1),f1(1)}=11
方案:(0,2),(1,1),(2,0)
F2(2)=max{f2(2),F1(1)+f2(1),F1(2)}=12
方案:(0,3),(1,2),(2,1),(3,0)
F2(3)=max{f2(3),F1(1)+f2(2), F1(2)+f2(1), F1(3)}=16
类似的计算
F2(4)=21, F2(5)=26
7.7 备忘录和解

八、0-1背包问题
给定n种物品和一背包。物品i的重量是wi,其价值为vi,背包的容量为C。问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
0-1背包问题是一个特殊的整数规划问题。

设所给0-1背包问题的子问题

算法复杂度分析:
从m(i,j)的递归式容易看出,算法需要O(nc)计算时间。当背包容量c很大时,算法需要的计算时间较多。例如,当c>2n时,算法需要Ω(n2n)计算时间。
最优值为m(i,j),即m(i,j)是背包容量为j,可选择物品为i,i+1,…,n时0-1背包问题的最优值。由0-1背包问题的最优子结构性质,可以建立计算m(i,j)的递归式如下。

8.1 算法改进
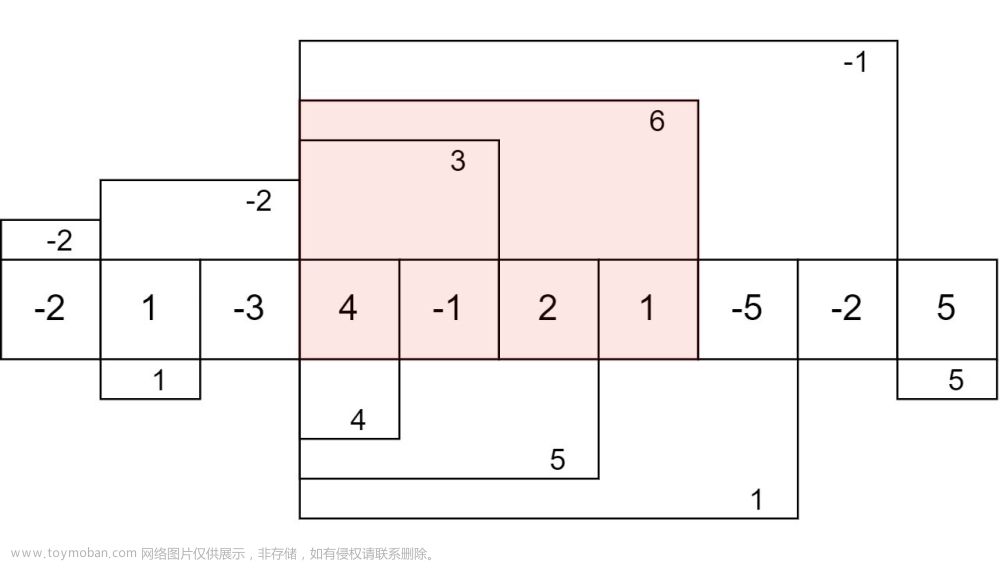
由m(i,j)的递归式容易证明,在一般情况下,对每一个确定的i(1≤i≤n),函数m(i,j)是关于变量j的阶梯状单调不减函数。跳跃点是这一类函数的描述特征。在一般情况下,函数m(i,j)由其全部跳跃点唯一确定。如图所示。
对每一个确定的i(1≤i≤n),用一个表p[i]存储函数m(i,j)的全部跳跃点。表p[i]可依计算m(i,j)的递归式递归地由表p[i+1]计算,初始时p[n+1]={(0,0)}。
8.2 一个例子
n=3,c=6,w={4,3,2},v={5,2,1}。







8.3 算法改进
函数m(i,j)是由函数m(i+1,j)与函数m(i+1,j-wi)+vi作max运算得到的。因此,函数m(i,j)的全部跳跃点包含于函数m(i+1,j)的跳跃点集p[i+1]与函数m(i+1,j-wi)+vi的跳跃点集q[i+1]的并集中。易知,(s,t)q[i+1]当且仅当wisc且(s-wi,t-vi)p[i+1]。因此,容易由p[i+1]确定跳跃点集q[i+1]如下q[i+1]=p[i+1](wi,vi)={(j+wi,m(i,j)+vi)|(j,m(i,j))p[i+1]}
另一方面,设(a,b)和(c,d)是p[i+1]q[i+1]中的2个跳跃点,则当ca且d<b时,(c,d)受控于(a,b),从而(c,d)不是p[i]中的跳跃点。除受控跳跃点外,p[i+1]q[i+1]中的其它跳跃点均为p[i]中的跳跃点。
由此可见,在递归地由表p[i+1]计算表p[i]时,可先由p[i+1]计算出q[i+1],然后合并表p[i+1]和表q[i+1],并清除其中的受控跳跃点得到表p[i]。
8.4 一个例子
n=5,c=10,w={2,2,6,5,4},v={6,3,5,4,6}。
初始时p[6]={(0,0)},(w5,v5)=(4,6)。因此,q[6]=p[6](w5,v5)={(4,6)}。p[5]={(0,0),(4,6)}。q[5]=p[5](w4,v4)={(5,4),(9,10)}。
从跳跃点集p[5]与q[5]的并集p[5]q[5]={(0,0),(4,6),(5,4),(9,10)}中看到跳跃点(5,4)受控于跳跃点(4,6)。将受控跳跃点(5,4)清除后,得到p[4]={(0,0),(4,6),(9,10)}。
q[4]=p[4](6,5)={(6,5),(10,11)}
p[3]={(0,0),(4,6),(9,10),(10,11)}
q[3]=p[3](2,3)={(2,3),(6,9)}
p[2]={(0,0),(2,3),(4,6),(6,9),(9,10),(10,11)}
q[2]=p[2](2,6)={(2,6),(4,9),(6,12),(8,15)}
p[1]={(0,0),(2,6),(4,9),(6,12),(8,15)}
p[1]的最后的那个跳跃点(8,15)给出所求的最优值为m(1,c)=15。
8.5 算法复杂度分析
上述算法的主要计算量在于计算跳跃点集pi。由于q[i+1]=p[i+1](wi,vi),故计算q[i+1]需要O(|p[i+1]|)计算时间。合并p[i+1]和q[i+1]并清除受控跳跃点也需要O(|p[i+1]|)计算时间。从跳跃点集p[i]的定义可以看出,p[i]中的跳跃点相应于xi,…,xn的0/1赋值。
因此,p[i]中跳跃点个数不超过2n-i+1。由此可见,算法计算跳跃点集p[i]所花费的计算时间为
从而,改进后算法的计算时间复杂性为O(2n)。当所给物品的重量wi(1≤i≤n)是整数时,|p[i]|≤c+1,(1≤i≤n)。在这种情况下,改进后算法的计算时间复杂性为O(min{nc,2n})。
九、最优二叉搜索树
9.1 二叉搜索树
(1)若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
(2)若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
(3)它的左、右子树也分别为二叉排序树在随机的情况下,二叉查找树的平均查找长度和logn是等数量级的。
9.2 二叉搜索树的期望耗费
搜索成功与不成功的概率:
二叉搜索树的期望耗费:
有 个节点的二叉树的个数为:穷举搜索法的时间复杂度为指数级:

9.3 二叉搜索树的期望耗费示例


9.4 最优二叉搜索树
最优二叉搜索树Tij的平均路长为pij,则所求的最优值为p1,n。由 最优二叉搜索树问题的最优子结构性质 可建立计算pij的递归式如下
记wi,jpi,j为m(i,j),则m(1,n)=w1,np1,n=p1,n为所求的最优值。计算m(i,j)的递归式为
注意到,
可以得到O(n2)的算法。文章来源:https://www.toymoban.com/news/detail-713256.html
十、小结
动态规划算法和分治法的相同点是什么?
动态规划算法和分治法的不同之处在哪里?
用“表”记录所有已有子问题的答案!避免重复计算,从而得到多项式时间复杂度。
动态规划通常用来计算“最优”解,不适合计算“合并”解。文章来源地址https://www.toymoban.com/news/detail-713256.html
到了这里,关于【算法分析与设计】动态规划(下)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!