本篇博客(上篇)先带大家学习递归方式进行三种遍历,
而在后续的(下篇)中将为大家详细讲解非递归的三种遍历方式。
目录
1、二叉树
2、二叉树的递归遍历
2.1、先序遍历
2.2、中序遍历
2.3、后序遍历

1、二叉树
二叉树(Binary tree)是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式,即使是一般的树也能简单地转换为二叉树,而且二叉树的存储结构及其算法都较为简单,因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树,且有左右之分。

2、二叉树的递归遍历
要了解二叉树的递归遍历写法,首先来了解一下递归序:
递归序就是按照先序遍历的顺序,遇到的所有结点按顺序排列,重复的结点也必须记录。

我们可以发现递归序中每个结点都会遇到三次。
这是因为当进入某一结点时,对该结点进行第一次操作,然后调用其左孩子结点,等左孩子结点结束调用时会返回自己,此时就可以对自己进行第二次操作,然后再调用其右孩子结点,等左孩子结点结束调用时又会返回自己,此时就可以对自己进行第三次操作,因为不管怎样,调用完孩子结点后终究会返回到父结点。
下面用代码来给大家举例子:
public static void f(Node head) {
//1
//1
f(head.left);
//2
//2
f(head.right);
//3
//3
}上面代码中:虽然此时代码中并没有对该节点进行其他操作,但是如果有的话
注释1部分就是该结点第一次被操作的时候,
注释2部分就是该结点第二次被操作的时候,
注释3部分就是该结点第三次被操作的时候。
2.1、先序遍历
对于所有子树,都是遵循【头左右】的顺序进行操作。
例如操作是打印结点,那么就应该先打印头结点,然后在打印左子树的结点,左子树的结点打印依然遵循【头左右】的操作顺序,然后再打印右子树的结点,操作也一样。
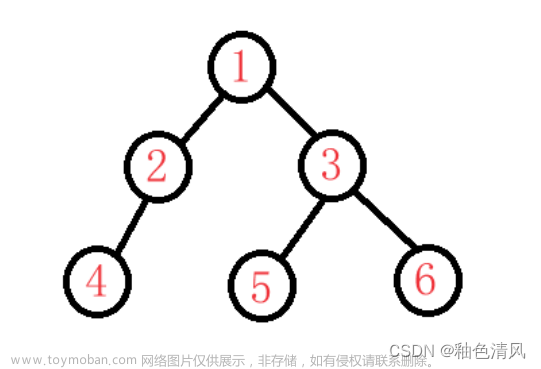
即先序遍历为:1,2,4,5,3,6,7。
对于1来说,是先打印了1再到2和3,对于3来说,是先打印了3再到6和7。

那么递归序在这里有什么用呢?递归序中第一次遇到该节点时打印结点,第二次第三次均不做任何操作,这就是先序遍历。如下图:

那么用代码表示就是在注释1处增加打印操作即是先序遍历。
public static void preOrderRecur(Node head) {
//1
if (head == null) {
return;
}
System.out.print(head.value + " "); //在第一次遇到该结点时打印
//1
preOrderRecur(head.left);
//2
//2
preOrderRecur(head.right);
//3
//3
}2.2、中序遍历
对于所有子树,都是遵循【左头右】的顺序进行操作。
例如操作是打印结点,那么就应该先打印头结点的左子树的所有结点,左子树的结点打印依然遵循【左头右】的操作顺序,然后返回到头节点此时对头节点进行打印,然后再打印右子树的结点,操作也一样。
即中序遍历为:4,2,5,1,6,3,7。
对于1来说,是先打印了2再到1然后到3,对于3来说,是先打印了6再到3然后到7。

递归序中第二次遇到该节点时打印结点,第一次第三次均不做任何操作,这就是中序遍历。如下图:

那么用代码表示就是在注释2处增加打印操作即是中序遍历。
public static void inOrderRecur(Node head) {
//1
if (head == null) {
return;
}
//1
inOrderRecur(head.left);
//2
System.out.print(head.value + " "); //在第二次遇到该结点时打印
//2
inOrderRecur(head.right);
//3
//3
}2.3、后序遍历
对于所有子树,都是遵循【左右头】的顺序进行操作。
例如操作是打印结点,那么就应该先打印头结点的左子树的所有结点,左子树的结点打印依然遵循【左右头】的操作顺序,返回到头节点不做操作,然后打印右子树的结点,操作也一样。最后返回到头节点此时对头节点进行打印。
即后序遍历为:4,5,2,6,7,3,1。
对于1来说,是先打印了2再到3然后到1,对于3来说,是先打印了6再到7然后到3。

递归序中第三次遇到该节点时打印结点,第一次第二次均不做任何操作,这就是后序遍历。如下图:

那么用代码表示就是在注释3处增加打印操作即是后序遍历。
public static void posOrderRecur(Node head) {
//1
if (head == null) {
return;
}
//1
posOrderRecur(head.left);
//2
//2
posOrderRecur(head.right);
//3
System.out.print(head.value + " "); 在第三次遇到该结点时打印
//3
}
如果觉得作者写的不错,求给博主一个大大的点赞支持一下,你们的支持是我更新的最大动力!文章来源地址https://www.toymoban.com/news/detail-713481.html
如果觉得作者写的不错,求给博主一个大大的点赞支持一下,你们的支持是我更新的最大动力!文章来源:https://www.toymoban.com/news/detail-713481.html
如果觉得作者写的不错,求给博主一个大大的点赞支持一下,你们的支持是我更新的最大动力!
到了这里,关于【算法与数据结构】二叉树的三种遍历代码实现(上)—— 用递归序知识点讲解的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!