线性回归的从零开始实现
在了解线性回归的关键思想之后，我们可以开始通过代码来动手实现线性回归了。 在这一节中，我们将从零开始实现整个方法， 包括数据流水线、模型、损失函数和小批量随机梯度下降优化器。 虽然现代的深度学习框架几乎可以自动化地进行所有这些工作，但从零开始实现可以确保我们真正知道自己在做什么。 同时，了解更细致的工作原理将方便我们自定义模型、自定义层或自定义损失函数。 在这一节中，我们将只使用张量和自动求导。 在之后的章节中，我们会充分利用深度学习框架的优势，介绍更简洁的实现方式。
%matplotlib inline
import random
import torch
from d2l import torch as d2l生成数据集
为了简单起见，我们将根据带有噪声的线性模型构造一个人造数据集。 我们的任务是使用这个有限样本的数据集来恢复这个模型的参数。 我们将使用低维数据，这样可以很容易地将其可视化。 在下面的代码中，我们生成一个包含1000个样本的数据集， 每个样本包含从标准正态分布中采样的2个特征。 我们的合成数据集是一个矩阵\(\mathbf{X}\in \mathbb{R}^{1000 \times 2}\)。
我们使用线性模型参数\(\mathbf{w} = [2, -3.4]^\top\)、\(b = 4.2\) 和噪声项\(\epsilon\)生成数据集及其标签：
(3.2.1)\[\mathbf{y}= \mathbf{X} \mathbf{w} + b + \mathbf\epsilon.\]
\(\epsilon\)可以视为模型预测和标签时的潜在观测误差。 在这里我们认为标准假设成立，即\(\epsilon\)服从均值为0的正态分布。 为了简化问题，我们将标准差设为0.01。 下面的代码生成合成数据集。
def synthetic_data(w, b, num_examples): #@save
"""生成y=Xw+b+噪声"""
X = torch.normal(0, 1, (num_examples, len(w)))
y = torch.matmul(X, w) + b
y += torch.normal(0, 0.01, y.shape)
return X, y.reshape((-1, 1))
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)注意，features中的每一行都包含一个二维数据样本， labels中的每一行都包含一维标签值（一个标量）。
features: tensor([1.4632, 0.5511])
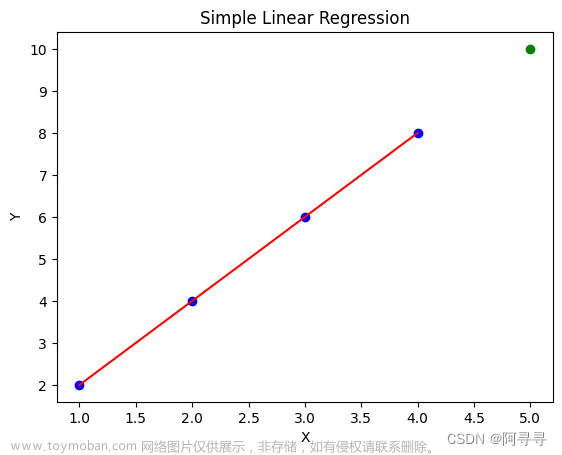
label: tensor([5.2498])通过生成第二个特征features[:, 1]和labels的散点图， 可以直观观察到两者之间的线性关系。文章来源：https://www.toymoban.com/news/detail-713499.html
d2l.set_figsize()
d2l.plt.scatter(features[:, (1)].detach().numpy(), labels.detach().numpy(), 1);
文章来源地址https://www.toymoban.com/news/detail-713499.html
到了这里，关于人工智能-线性回归的从零开始实现的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
