上篇:【算法与数据结构】二叉树的三种遍历代码实现(上)—— 用递归序知识点讲解_Hacynn的博客-CSDN博客https://blog.csdn.net/zzzzzhxxx/article/details/133609612?spm=1001.2014.3001.5502
目录
前言
1、先序遍历
1.1、详细图解描述
1.2、先序遍历非递归代码实现
2、中序遍历
2.1、详细图解描述
2.2、中序遍历非递归代码实现
3、后序遍历
3.1、详细图解描述
3.2、后序遍历非递归代码实现

前言
在上篇当中给大家介绍了二叉树的先序遍历、中序遍历以及后序遍历的递归写法。递归的系写法主要是理解递归序,只要递归序能够理解清楚,就能够很轻易地理解和书写递归实现三次遍历。
任何递归函数都可以改成非递归函数,因为递归函数不是什么玄学,只是递归时系统帮忙解决了压栈问题。那么不用递归方式的话只要自己手动进行压栈依然可以完成递归能够实现的功能。
那么在接下来的下篇中,我将带大家审深入学习二叉树三种遍历的非递归写法,也是二叉树遍历的代码中的重点内容,因为递归方式的代码非常好实现,因此在面试时常常会考大家的是非递归的写法。
1、先序遍历
先说结论:首先准备一个栈,将头结点入栈后,执行循环操作:
- 从栈中弹出一个结点记为cur。
- 对cur进行打印(或者是处理)操作。
- 如果cur有右孩子的话,则将cur的右孩子入栈。
- 如果cur有左孩子的话,则将cur的左孩子入栈。(即先右再左)注意区分此时的入栈顺序和递归实现遍历时的打印顺序的不同,不要搞混淆。
- 周而复始。
压栈顺序:头右左
1.1、详细图解描述
下面进行详细步骤描述:
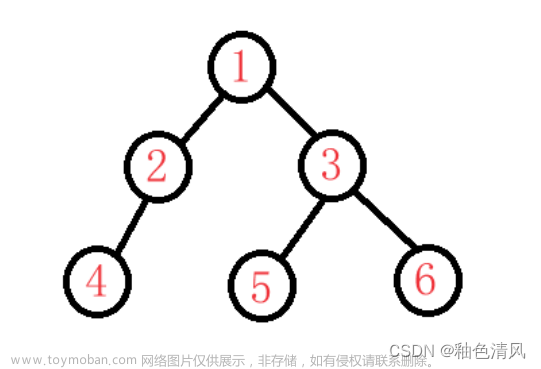
首先先把头结点进栈,即1结点入栈。

从栈中弹出一个结点记为cur,此时的cur即为1。对cur进行打印(或者其他处理)操作,如果cur有孩子的话,则将cur的右节点和左节点按右左顺序入栈。即此时 结点3 和 结点2 入栈。

周而复始,再次从栈中弹出一个结点记为cur,此时的cur即为2。对cur进行打印(或者其他处理)操作,并将cur的孩子按右左顺序入栈。即此时 结点5 和 结点4 入栈。

周而复始,栈中弹出结点4记为cur,打印cur,并压栈cur左右孩子结点,但是此时cur(也就是4结点)并没有左右孩子结点了,所以不进行压栈操作。

周而复始,栈中弹出结点5记为cur,打印cur,5和4一样没有孩子节点,所以不进行压栈。

周而复始,栈中弹出结点3记为cur,打印cur,将孩子结点6和7入栈。

剩下的操作就都是周而复始的操作了,这里篇幅原因就不在演示了。可以看到打印出来的顺序就是先序遍历的顺序。
1.2、先序遍历非递归代码实现
public static void preOrderUnRecur(Node head) {
if (head != null) {
Stack<Node> stack = new Stack<Node>(); //首先准备一个栈stack
stack.add(head); //将头结点入栈
while (!stack.isEmpty()) { //当栈不为空时执行循环
head = stack.pop(); //从栈中弹出结点
System.out.print(head.value + " "); //打印(或是处理)
if (head.right != null) { //右孩子不为空,则入栈
stack.push(head.right);
}
if (head.left != null) { //左孩子不为空,则入栈(必须遵循先右后左的入栈顺序)
stack.push(head.left);
}
}
}
}2、中序遍历
先说结论:首先准备一个栈,执行循环操作:
- 先将整棵树的左边界的所有结点依次入栈。
- 依次从栈中弹出结点记为cur,并打印(或其他操作)cur。依次判断cur是否有右子树,有则将右子树的整棵树左边界的所有结点依次入栈。
- 周而复始。
压栈顺序:(左全)右
2.1、详细图解描述
下面进行详细步骤描述:
首先将整颗数的左边界依次入栈,即1,2,4。

从栈用弹出结点4记为cur,打印cur并判断右子树是否存在,此时没有则继续从栈用弹出结点2记为cur并打印。

判断cur的右子树是否存在,此时右子树存在,则以结点5为整棵树的头结点,将整棵树的左边界的所有结点依次入栈,这里的左边界只有5结点一个,即将5结点入栈。

从栈用弹出结点5记为cur,打印cur,此时cur不存在右子树,则继续从栈中弹出结点1记为cur并打印。

此时cur(即结点1)存在右子树,则以结点3为整棵树的头结点,将整棵树的左边界的所有结点依次入栈,即3和6。

继续从栈中弹出结点6记为cur并打印,此时结点6没有右子树,则继续从栈中弹出结点3并打印。

最后结点3存在右子树,右子树的左边界只有7,将7入栈。然后从栈中弹出7并打印,7没有孩子节点,不操作。当再从栈中弹出结点时发现已空,则结束循环。

2.2、中序遍历非递归代码实现
public static void inOrderUnRecur(Node head) {
if (head != null) {
Stack<Node> stack = new Stack<Node>(); //栈stack
while (!stack.isEmpty() || head != null) { //栈不为空或者此时的头结点不为空
if (head != null) {
//如果head不为空,则入栈,然后head指向下一个左孩子结点,继续判断是否为空,不为空继续执行
stack.push(head);
head = head.left;
} else {
//当为空时从栈中弹出结点head,然后打印出head,并将head指向head的右孩子结点
head = stack.pop();
System.out.print(head.value + " ");
head = head.right;
}
}
}
}3、后序遍历
先说结论:首先准备两个栈(一个遍历栈,一个收集栈),将头结点压栈进遍历栈后,执行循环操作:
- 从遍历栈中弹出一个结点记为cur。
- 将cur压栈进收集栈中。
- 如果cur有左孩子的话,则将cur的左孩子压栈进遍历栈。
- 如果cur有右孩子的话,则将cur的右孩子压栈进遍历栈。(即先左再右),注意与先序非递归遍历进行区分。
- 周而复始。
最后当遍历栈中再无结点时,将收集栈中的内容全部出栈,出栈顺序即为后序遍历顺序。
压栈顺序:头左右
3.1、详细图解描述
下面进行详细步骤描述:
首先先把头结点入遍历栈,即1结点入遍历栈。

从遍历栈中弹出一个结点记为cur,此时的cur即为1。然后将cur入收集栈。如果cur有孩子的话,则将cur的左节点和右节点按左右顺序入遍历栈。即此时 结点2 和 结点3 入遍历栈。

周而复始,从遍历栈中弹出一个结点记为cur,此时的cur即为3。然后将cur入收集栈。如果cur有孩子的话,则将cur的左节点和右节点按左右顺序入遍历栈。即此时 结点6 和 结点7 入遍历栈。

周而复始,从遍历栈中弹出结点7记为cur,然后将cur入收集栈。此时cur没有左右孩子,所以不操作。
接下来的结点6也和结点7一样,从遍历栈中弹出后直接入收集栈。

周而复始,从遍历栈中弹出结点2记为cur,然后将cur入收集栈。将cur的孩子结点4,5分别入遍历栈。

最后遍历栈中的5和4都没有孩子结点,因此全部出栈并入收集栈。

此时将收集完的收集栈依次出栈并打印,得到的序列就是后序遍历。

3.2、后序遍历非递归代码实现
public static void posOrderUnRecur(Node head) {
if (head != null) {
Stack<Node> s1 = new Stack<Node>(); //遍历栈
Stack<Node> s2 = new Stack<Node>(); //收集栈
s1.push(head); //头结点入遍历栈
while (!s1.isEmpty()) { //遍历栈不为空时遍历
head = s1.pop(); //从遍历栈中出栈
s2.push(head); //将出栈结点入收集栈
if (head.left != null) { //当左孩子存在时入遍历栈
s1.push(head.left);
}
if (head.right != null) { //当右孩子存在时入遍历栈(必须遵循先左后右的入栈顺序)
s1.push(head.right);
}
}
while (!s2.isEmpty()) { //当遍历栈结束后,将收集栈中的所有结点挨个打印
System.out.print(s2.pop().value + " ");
}
}
} 
如果觉得作者写的不错,求给博主一个大大的点赞支持一下,你们的支持是我更新的最大动力!文章来源地址https://www.toymoban.com/news/detail-713634.html
如果觉得作者写的不错,求给博主一个大大的点赞支持一下,你们的支持是我更新的最大动力!文章来源:https://www.toymoban.com/news/detail-713634.html
如果觉得作者写的不错,求给博主一个大大的点赞支持一下,你们的支持是我更新的最大动力!
到了这里,关于【算法与数据结构】二叉树的三种遍历代码实现(下)—— 非递归方式实现(大量图解)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!