汉诺塔（Tower of Hanoi）--------递归思路-Toy模板网

这篇具有很好参考价值的文章主要介绍了汉诺塔（Tower of Hanoi）--------递归思路。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

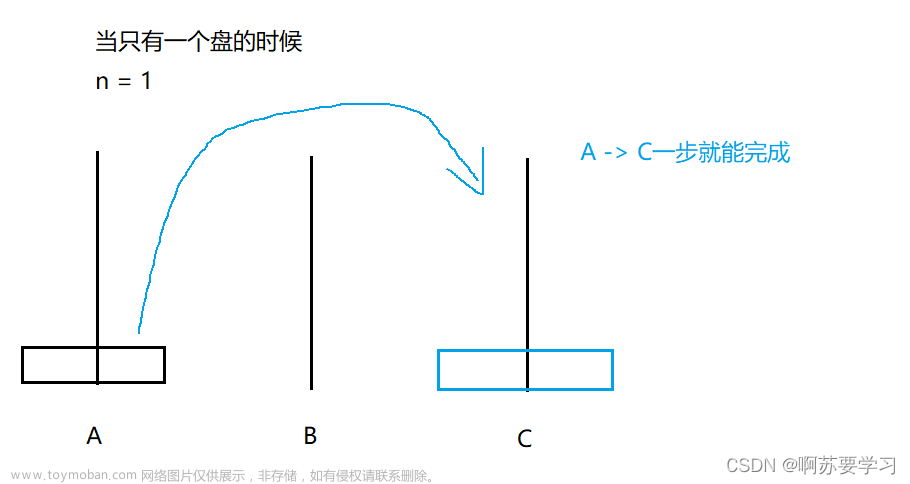
汉诺塔问题简介：

有三根相邻的柱子，标号为A,B,C，A柱子上从下到上按金字塔状叠放着n个不同大小的圆盘，要把所有盘子一个一个移到柱子C上，并且每次移动，同一根柱子上都只能是大盘子在下，小盘子在上，请问至少需要多少次移动？

汉诺塔问题分析：

1. 若只有1个圆盘，就只需要移动 1 次，即 A → C;

2. 若有两个圆盘，则需要移动 3 次，即 A→B,A→C,B→C;

汉诺塔递归,算法,c语言

3. 若有三个圆盘，则需要移动 7 次，即 A→ C,A→ B,C→ B,A→ C,B→ A,B→ C,A→ C

汉诺塔递归,算法,c语言

依此类推.......

汉诺塔问题的递归思路：

将 n 个圆盘分为 n-1 （即除最低层的圆盘）与 1 （即最底层的圆盘），将n-1个圆盘移动到中转位置，将1移动到目的位置，再将 n-1 分为（n-1）- 1 与 1，将（n-1）- 1 移动到中转位置，将1移动到目的位置，依次类推......

代码如下:

#include<stdio.h>
//打印每一步的操作
void move(char a, char b)
{
	printf(" %c -> %c ", a, b);
}
//n:有几个盘子
//a:起始位置
//b:中转位置
//c:目的位置
void hbt(int n, char a, char b, char c)
{
	if (n == 1)
		move(a, c);
	else//n>=2时
	{
		hbt(n - 1, a, c, b);
        //此时n-1的起始位置是a,中转位置是c,目的位置是b
		move(a, c);
        //将 1 从起始位置 a 移动到目的位置 c
		hbt(n - 1, b, a, c);
        //将 n-1 从起始位置 b,通过中转位置a,移动到目的位置 c
	}

}
int main()
{
	hbt(3, 'A', 'B', 'C');
    //3就代表有3个盘子，可修改
	return 0;
}

图示如下：

汉诺塔递归,算法,c语言