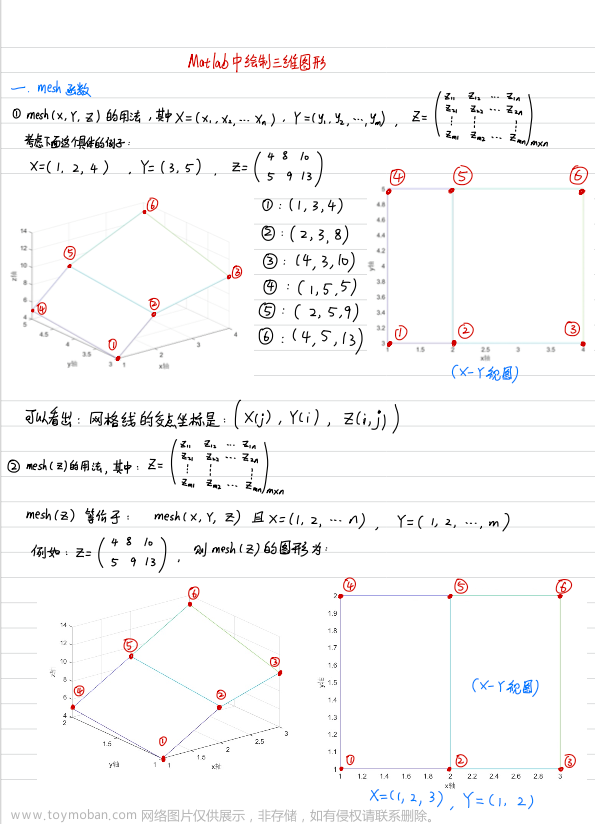
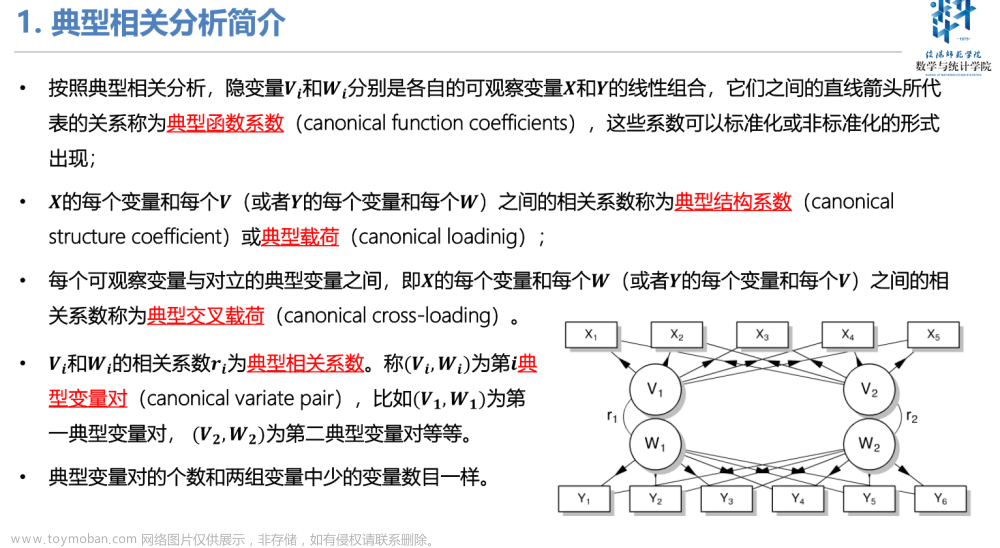
本帖总结一些经典的图论问题，通过MATLAB如何计算答案。近期在复习考研，以此来巩固一下相关知识——虽然考研肯定不能用MATLAB代码哈哈，不过在实际应用中解决问题还是很不错的，比C++易上手得多~
此外，本帖图论中非常重要的知识点——最小生成树。作为数据结构的理论知识，Prim算法和克鲁斯卡尔算法的思想此处博主不详细介绍，建议在阅读本帖前熟练掌握。
最后，本贴介绍最短路径的计算，实现方式为迪杰斯特拉算法；对于弗洛伊德算法，区别在于计算了所有结点之间的最短路径，考虑到MATLAB计算的便捷性，计算时只需要反复使用迪杰斯特拉即可，暂不介绍弗洛伊德的实现
（一）基本操作基础
图论中的图（Graph）是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用点代表事物，用连接两点的线表示相应两个事 物间具有这种系。
1.有向图：弧是顶点的有序对，通过grapi（s,t）函数绘制。s和t分别是两个边两端的点集
无向图：边是顶点的无序对，通过digrapi（s,t)函数绘制。
% 函数graph(s,t)：可在 s 和 t 中的对应节点之间创建边，并生成一个图
s=[1 1 2 2 2 4 4 3 3 5];
t=[2 3 3 4 5 3 5 5 6 6];
%s和t为端点的集合
G1=graph(s,t);
plot(G1)
%绘制无向图
G2=digraph(s,t);
%绘制有向图
plot(G2)2.领接矩阵
无向图的领接矩阵必须是对称的，意义为两端点间相互建立联系；而有向图则仅需要从头到尾处建立连接即可（列向为起点，行向为终点）
如上图，对于一个相同的邻接矩阵，画出的有向图与无向图形状差距在于边数——对于对称的邻接矩阵，其画为有向图后两节点之间必定各有两条边。
A1=[1,0,1,1,1,0;
0,0,0,0,1,1;
1,0,0,1,0,1;
1,0,1,0,0,0;
1,1,0,0,0,0;
0,1,1,0,0,0;
];
G1=graph(A1);
%plot(G1)
G2=digraph(A1);
plot(G2)3.增加与删除
- addedge：添加新边
- rmedge：删除边
- addnode：添加节点
- rmnode：删除指定节点
- numegdes：边的数量
- numnodes：节点的数量
此处演示一下增加节点的效果：
s3=[7,7,7,3,3,1,6];
t3=[3,1,6,1,6,6,6];
G3=graph(s3,t3);
G3=G3.addnode(3);
G3=G3.addedge(2,4);
plot(G3) 
4.添加权重and命名结点
s=[1 1 2 3 3 5 6 7 5 2];
t=[2 4 7 4 6 8 7 8 6 8];
weights=[13 19 25 17 11 10 92 29 9 3 ];
names={'H' 'Y' '+' '&' 'J' 'S' 'L' '32'};
G=graph(s,t,weights,names);
plot(G,'EdgeLabel',weights)（至于一些修改图片样式的操作，本贴暂不更新，后期抽空会出绘图专题~）
（二）计算最小生成树
对于无向带权图，在MATLAB中可以直接以邻接矩阵的方式创建出来，如下：
A=[0 20 0 0 15 0;
20 0 20 60 25 0;
0 20 0 30 18 0;
0 60 30 0 35 10;
15 25 18 35 0 15;
0 0 0 10 15 0];
G=graph(A);但是这种创建方式对于可视化并不是很友好——无法在图上显示每条边对应的权值，因此采用下面的方式创建：
s=[1 1 2 2 2 3 3 4 4 5];
t=[2 5 3 4 5 4 5 5 6 6];
weights=[20 15 20 60 25 30 18 35 10 15];
G=graph(s,t,weights);
plot(G,'EdgeLabel',weights);创建出的带全无向图如下：
首先我们先用普利姆算法手写一遍，得出的答案如下：
然后用MATLAB计算并可视化，用到内置函数minspantree：
T=minspantree(G);
plot(T);计算结果如下：
如图，和博主手算的略微有区别：其实是因为1——2与2——3两条边的权值一致，所以最后找到的结点2无论和结点1还是结点3连接都正确~
（三）Dijkstra算法计算最短路径
迪杰斯特拉算法的思想，通俗的归纳来说就是：从当前结点出发，寻找一个未与当前简历连接——且路径最小的点作为下一个寻找到的地址。有关结点是否建立连接，需要一个如下的矩阵来辅助记录。
若还未建立连接，则将前驱标记为-1，距离记录为无穷~
至于Distance内，存放的是起点到当前结点的最短距离，这一距离可能会不断更新，直到寻找到最短的路径为止~
实现的具体底代码：
- 第一种：
[P,d] = shortestpath(G, 9, 4)如上代码中，P表示的9与4节点之间最短路径经过的结点，而d保存的是最短路径值的总和~
- 第二种：
D = distances(G); D(1,2); D(9,4);如上代码中，D是一个存储了任意两结点之间最短路径的矩阵，通过索引访问的方式，即可求出任意两点的最短路径~
此外，如下是计算求出指定节点指定距离内部的全部结点的实现方式：
[nodeIDs,dist] = nearest(G, 2, 10); 注意，上述几个函数从2017a版本后才能全部使用
如下是创建图并计算图的具体实现方式：
s = [9 9 1 1 2 2 2 7 7 6 6 5 5 4];
t = [1 7 7 2 8 3 5 8 6 8 5 3 4 3];
w = [4 8 3 8 2 7 4 1 6 6 2 14 10 9];
G = graph(s,t,w);plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2)
set( gca, 'XTick', [], 'YTick', [] );
[P,d] = shortestpath(G, 9, 4);
myplot = plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2);
highlight(myplot, P, 'EdgeColor', 'g') ; 结果如下，绿色即为最短路径：文章来源：https://www.toymoban.com/news/detail-713725.html
文章来源地址https://www.toymoban.com/news/detail-713725.html
到了这里，关于MATLAB——图论合集的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
