目录
1 二分查找算法
2 线性查找算法
3 哈希查找算法
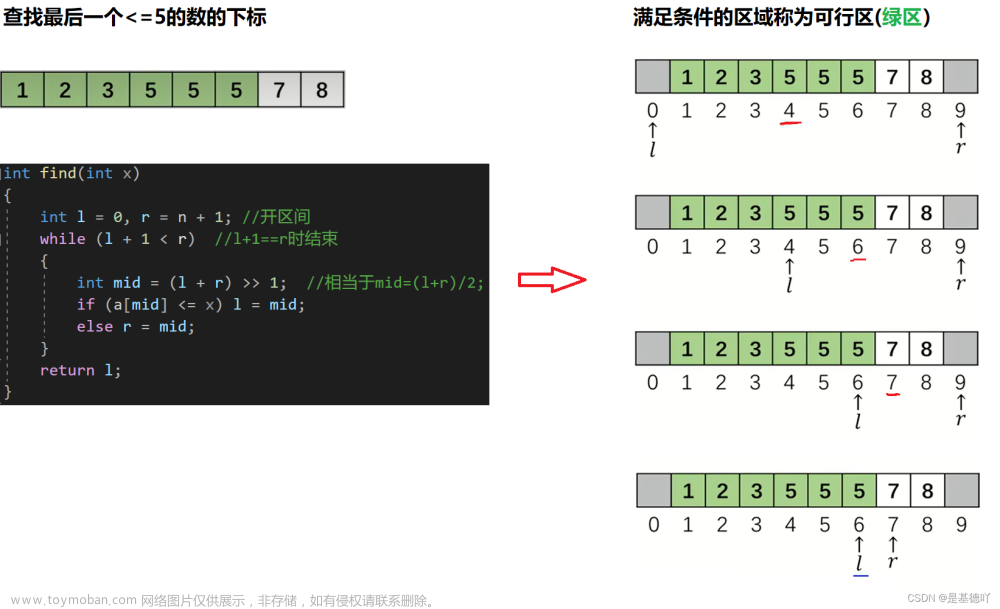
1 二分查找算法
二分查找(Binary Search)是一种用于在有序数据集合中查找特定元素的高效算法。它的工作原理基于将数据集合分成两半,然后逐步缩小搜索范围,直到找到目标元素或确定目标元素不存在。

以下是二分查找的工作原理的详细说明:
有序数据集合:首先,数据集合必须是有序的,通常是按升序或降序排列的。这一点非常重要,因为二分查找的核心思想是根据中间元素与目标元素的大小关系来确定搜索范围。
初始化指针:初始化两个指针,一个指向数据集合的第一个元素(左指针),另一个指向最后一个元素(右指针)。
确定中间元素:计算左指针和右指针的中间位置,即
(left + right) // 2。这将确定搜索区域的中间元素。比较中间元素:将中间元素与目标元素进行比较:
- 如果中间元素等于目标元素,搜索成功,返回中间元素的索引。
- 如果中间元素大于目标元素,说明目标元素应该在左半部分,将右指针移到中间元素的左侧一位,即
right = mid - 1。- 如果中间元素小于目标元素,说明目标元素应该在右半部分,将左指针移到中间元素的右侧一位,即
left = mid + 1。重复步骤3和4:在每次比较后,缩小搜索范围,继续比较直到找到目标元素或搜索范围为空(即左指针大于右指针)。
返回结果:如果找到目标元素,返回它的索引;如果搜索范围为空仍未找到目标元素,返回一个指示未找到的值(通常是 -1)。
以下是一个简单的示例,演示如何使用二分查找在有序数组中查找目标元素:
def binary_search(arr, target):
left, right = 0, len(arr) - 1 # 初始化左右指针,分别指向数组的起始和结束位置
while left <= right: # 当左指针不大于右指针时,继续搜索
mid = (left + right) // 2 # 计算中间位置
if arr[mid] == target: # 如果中间元素等于目标元素,搜索成功
return mid # 返回中间元素的索引
elif arr[mid] < target: # 如果中间元素小于目标元素,说明目标在右半部分
left = mid + 1 # 移动左指针到中间元素的右侧一位
else: # 否则,目标在左半部分
right = mid - 1 # 移动右指针到中间元素的左侧一位
return -1 # 如果搜索范围为空仍未找到目标元素,返回 -1 表示未找到
# 示例用法
sorted_list = [1, 2, 3, 4, 7, 9]
target_element = 7
result = binary_search(sorted_list, target_element)
if result != -1:
print(f"元素 {target_element} 在索引 {result} 处找到。")
else:
print("元素未找到。")
上述代码演示了如何使用二分查找在有序列表
sorted_list中查找目标元素7。根据工作原理,二分查找的时间复杂度为 O(log n),其中 n 是数据集合的大小,这使得它非常适合在大型有序数据集合中查找目标元素。
2 线性查找算法
线性查找(Linear Search)是一种简单的搜索算法,也称为顺序查找。它的工作原理是逐个遍历数据集合中的元素,直到找到匹配的元素或遍历整个集合。
原理:
从数据集合的第一个元素开始,逐个检查每个元素,直到找到匹配的元素或遍历整个集合。
如果找到与目标元素匹配的元素,返回该元素的索引(位置)。
如果遍历整个集合都没有找到匹配的元素,返回特定的“未找到”值(通常是 -1)。
以下是线性查找的原理示例:
数据集合: [2, 4, 7, 1, 9, 3]
要查找的元素: 7
初始状态:
↓
[2, 4, 7, 1, 9, 3]
^
第一次比较:元素 2 与目标 7 不匹配,继续下一个元素。
↓
[2, 4, 7, 1, 9, 3]
^
第二次比较:元素 4 与目标 7 不匹配,继续下一个元素。
↓
[2, 4, 7, 1, 9, 3]
^
第三次比较:元素 7 与目标 7 匹配,找到了目标元素。
↓
[2, 4, 7, 1, 9, 3]
^
目标元素 7 找到在索引 2 处。
上述示意图演示了如何使用线性查找在给定的数据集合中查找目标元素 7。算法从数据集合的第一个元素开始逐个比较,直到找到匹配的元素或遍历整个集合。
这个示意图反映了线性查找的工作原理,即逐个遍历数据元素以寻找匹配项。如果目标元素存在于数据集合中,线性查找将找到该元素的索引。如果目标元素不存在,则遍历整个数据集合后返回特定的未找到值(通常是 -1)。
以下是一个Python线性查找示例代码:
def linear_search(arr, target):
"""
线性查找函数
Parameters:
- arr: 待查找的列表
- target: 要查找的目标元素
Returns:
- 如果找到目标元素,返回其索引;否则返回 -1。
"""
for i in range(len(arr)): # 遍历列表中的每个元素
if arr[i] == target: # 如果当前元素与目标元素匹配
return i # 返回匹配元素的索引
return -1 # 如果遍历完整个列表未找到匹配元素,返回 -1 表示未找到
# 示例用法
my_list = [2, 4, 7, 1, 9, 3]
target_element = 7
result = linear_search(my_list, target_element) # 调用线性查找函数
if result != -1:
print(f"元素 {target_element} 在索引 {result} 处找到。")
else:
print("元素未找到。")
在上述代码中,
linear_search函数用于执行线性查找。它接受两个参数:要查找的列表arr和目标元素target。函数逐个遍历列表中的元素,如果找到匹配的元素,则返回匹配元素的索引;如果遍历完整个列表都没有找到匹配元素,则返回 -1 表示未找到。示例用法演示了如何调用
linear_search函数来查找目标元素7在列表my_list中的位置。如果找到目标元素,程序将打印出找到的索引,否则打印 "元素未找到。"。
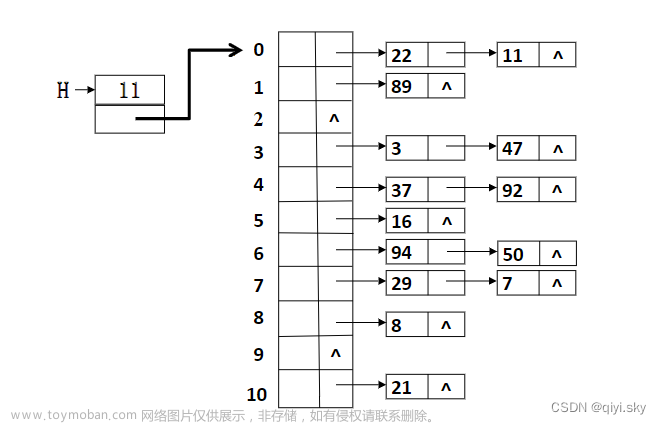
3 哈希查找算法
哈希查找(Hash Search)是一种高效的搜索算法,它利用哈希函数将键映射到存储位置,并在该位置查找目标元素。哈希查找适用于快速查找和检索,特别适用于大型数据集合。以下是哈希查找的详细解释和示例:
工作原理:
哈希表:哈希查找的核心是哈希表,它是一个数据结构,由键-值对组成。哈希表内部使用哈希函数将键转换为存储位置(索引),然后将键和值存储在该位置。
哈希函数:哈希函数接受一个键作为输入,并生成一个索引(位置),通常是一个整数。好的哈希函数应该具有以下特性:
- 对于相同的输入键,始终生成相同的索引。
- 将不同的输入键均匀地映射到不同的索引,以减少冲突。
- 生成的索引应尽可能分散,以降低冲突的可能性。
查找过程:要查找目标元素,哈希函数首先计算目标元素的哈希值(索引),然后在哈希表的该位置查找对应的值。如果找到匹配的值,查找成功;否则,表示未找到目标元素。
示例代码:
以下是一个使用Python的哈希查找示例代码,我们将使用字典作为哈希表来演示:
# 创建一个哈希表(字典)
my_dict = {'apple': 3, 'banana': 2, 'cherry': 5, 'date': 1, 'grape': 4}
# 要查找的目标键
target_key = 'banana'
# 使用哈希查找
if target_key in my_dict:
value = my_dict[target_key]
print(f"The value of {target_key} is {value}")
else:
print(f"{target_key} not found")
在上述示例中,我们首先创建了一个哈希表
my_dict,其中包含键-值对。然后,我们定义了要查找的目标键target_key为'banana'。通过使用哈希查找,我们可以直接访问哈希表中的值,而不需要逐个遍历整个集合。如果目标键存在于哈希表中,我们将获得与该键关联的值。请注意,哈希查找的效率非常高,因为它通常具有常量时间复杂度 O(1)。然而,哈希函数的设计和解决冲突的方法对算法的性能至关重要。合适的哈希函数和处理冲突的方法可以确保高效的哈希查找。
4 应用
-
线性查找(Linear Search):
- 工作原理:逐个遍历数据集合,查找目标元素。
- 应用:适用于小型无序数据集合,或当数据无序且不频繁查找时。常见于简单的列表或数组。
-
二分查找(Binary Search):
- 工作原理:适用于有序数据集合,将数据集合分成两半,逐步缩小搜索范围。
- 应用:适用于大型有序数据集合,如数组或有序列表。常见于数据库索引等高效查找场景。
-
哈希查找(Hash Search):文章来源:https://www.toymoban.com/news/detail-714056.html
- 工作原理:通过哈希函数将键映射到存储位置,查找时直接访问该位置。
- 应用:适用于快速查找,如字典、散列表(哈希表)等数据结构。常用于处理大量数据的快速索引。
-
二叉搜索树查找(Binary Search Tree Search):文章来源地址https://www.toymoban.com/news/detail-714056.html
- 工作原理:通过二叉搜索树的有序性,在左子树或右子树中查找目标元素。
- 应用:适用于维护有序数据集合,如数据库索引、字典实现等
到了这里,关于【Python查找算法】二分查找、线性查找、哈希查找的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!