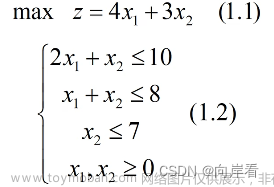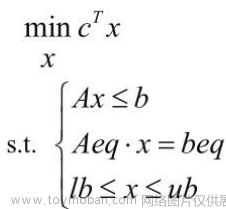数学建模——线性规划篇（lingo软件实现）-Toy模板网

这篇具有很好参考价值的文章主要介绍了数学建模——线性规划篇（lingo软件实现）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

（线性规划）习题

1.某工厂利用两种原料甲、乙生产A1，A2，A3三种产品. 每月可供应的原料数量（单位：t）、每万件产品所需各种原料的数量及每万件产品的价格如下表所示：

原料	每万件产品所需原料/t			每月原料供应量/t
原料	A1	A2	A3	每月原料供应量/t
甲	4	3	1	180
乙	2	6	3	200
价格/万元	12	5	4

试制定每月最优生产计划，使得总收益最大；

代码：

model:

max=12*x1+5*x2+4*x3;

4*x1+3*x2+x3<180;

2*x1+6*x2+3*x3<200;

end

结果分析：

lingo求解线性规划问题,数学建模,lingo,线性规划,数学建模,动态规划,线性回归,算法

有结果报告可知当A1，A2，A3分别生产34万件，0万件，44万件时受益最大为584.00万元。

对求得的最优生产计划进行灵敏度分析.

lingo求解线性规划问题,数学建模,lingo,线性规划,数学建模,动态规划,线性回归,算法

由灵敏度分析可知当A1的价格在[2.78，16.00]范围内A2的价格在[5.00，10.80]范围内A3的价格在[3.00，16.00]范围内时最优解不变。甲原料的供应量在[66.78，400.00]时，乙原料在[90.00，540.00]时最优解不变。

2.某医院负责人每日至少需要下列数量的护士：

班次	时间	最少护士数
1	6时—10时	60
2	10时—14时	70
3	14时—18时	60
4	18时—22时	50
5	22时—02时	20
6	02时—06时	30

每班的护士在职班开始时向病房报道，连续工作8个小时. 医院领导为满足每班所需要的护士数，最少需雇用多少护士？

代码：

min=x1+x2+x3+x4+x5+x6;

x1>=60;

x1+x2>=70;

x2+x3>=60;

x3+x4>=50;

x4+x5>=20;

x5+x6>=30;

结果分析：

lingo求解线性规划问题,数学建模,lingo,线性规划,数学建模,动态规划,线性回归,算法

有最优解可知至少要雇佣150个护士。

3.某工厂生产A1，A2两种型号的产品都必须经过零件装配和检验两道工序，如果每天可用于零件配件的工时只有100h，可用于检验的工时只有120h，各型号产品每件需占用各工序时数和可获得的利润如下表所示：

	产品			可用工时
工序	A1	A2	A3	可用工时
装配	2	3	4	100
检验	4	2	2	120
利润/元	6	4	5

试写出此问题的数学模型，并求出最优生产方案.

代码：

model:

max=6*x1+4*x2;

2*x1+3*x2<100;

4*x1+2*x2<120;

End

结果分析：

lingo求解线性规划问题,数学建模,lingo,线性规划,数学建模,动态规划,线性回归,算法

最优生产方案为A1，A2，产品各生产20件，20件，获益最大。

对产品A1的利润进行灵敏度分析.

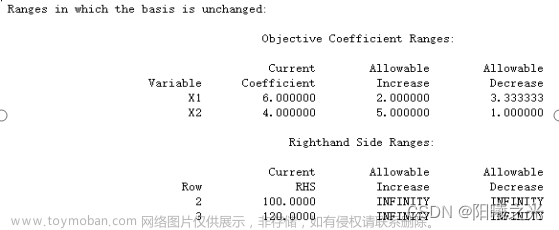
lingo求解线性规划问题,数学建模,lingo,线性规划,数学建模,动态规划,线性回归,算法

当A1产品的利润价格控制在[2.67,8]范围内时最优解不变。

如果工厂试制了A3型产品，每件A3产品需装配工时4h，检验工时2h，可获利5元，那么该产品是否应投入生产?

代码：

model:

max=6*x1+4*x2+5*x3;

2*x1+3*x2+4*x3<100;

4*x1+2*x2+2*x3<120;

End

结果分析：

lingo求解线性规划问题,数学建模,lingo,线性规划,数学建模,动态规划,线性回归,算法

当A3投入生产时最优解的目标值为206>200，所以应该投入生产。

4.有两个厂A、B，每月进煤分别不少于60t、100t，它们担负供应三个居民区用煤任务，这三个居民区每月需要用煤分别为45t、75t、40t. A厂离这三个居民区分别为10km、5km、6km，B厂离这三个居民区分别为4km、8km、15km，问这两煤矿厂如何分配供煤，才能使总运输量最小？

解：设A厂向三地分别供煤x1,x2,x3;B厂向三地送煤y1,y2,y3.

代码：

model:

min=10*x1+5*x2+6*x3+4*y1+8*y2+15*y3;

x1+x2+x3>60;

y1+y2+y3>100;

x1+y1=45;

x2+y2=75;

x3+y3=40;

End

结果分析：

lingo求解线性规划问题,数学建模,lingo,线性规划,数学建模,动态规划,线性回归,算法

即A厂分别送0t,20t,40t,,B厂分别送45t,55t,0t这样运输量最小。

补充：

Lingo是一种专业的线性和非线性优化软件，常用于解决复杂的优化问题。以下是一般使用Lingo软件的基本步骤：

安装Lingo软件：请按照官方提供的安装指南，下载并安装Lingo软件到您的计算机上。

启动Lingo软件：双击打开Lingo应用程序，在界面中选择或创建一个新的项目。

在Lingo软件的主界面上，您可以看到一系列菜单和工具栏选项。
点击菜单栏中的 "File"（文件）选项，然后选择 "New"（新建）。
在弹出的对话框中，您可以选择创建一个空项目或者打开一个现有项目。如果是首次使用Lingo，选择 "Empty Project"（空项目）。
接下来，您需要为项目指定一个名称。输入相应的名称，并确定保存位置。
完成上述步骤后，Lingo将为您创建一个新的项目，并在界面中显示项目名称和相关信息。

通过以上步骤，您已经成功创建了一个新的Lingo项目，接下来就可以开始定义变量、设定目标函数和添加约束条件，进行优化和分析了。请注意，具体操作可能会根据不同版本的Lingo软件略有不同，但大体思路应该是相似的。

定义变量：在Lingo中，您需要定义您要优化的变量。根据您的问题，可以是整数型、实数型、二元型等。

在Lingo的项目界面上，您可以看到一个"Variables"（变量）选项卡或类似的选项。
点击"Variables"选项卡，进入变量定义界面。
在变量定义界面，您可以看到现有变量列表（如果有的话）以及添加新变量的选项。
点击"Add"、"New Variable"或类似的按钮，以添加新的变量。
在弹出的对话框中，您需要为变量指定名称、选择变量类型和范围等属性。
- 如果您的变量是整数型，您可以选择"Integer"。
- 如果您的变量是实数型，您可以选择"Real"。
- 如果您的变量是二元型，即只能取0或1的变量，您可以选择"Binary"。
您还可以指定变量的上下限范围，以便约束变量的取值范围。
完成上述设置后，点击"OK"或"Add"按钮确认添加变量。