XGBoost模型详解

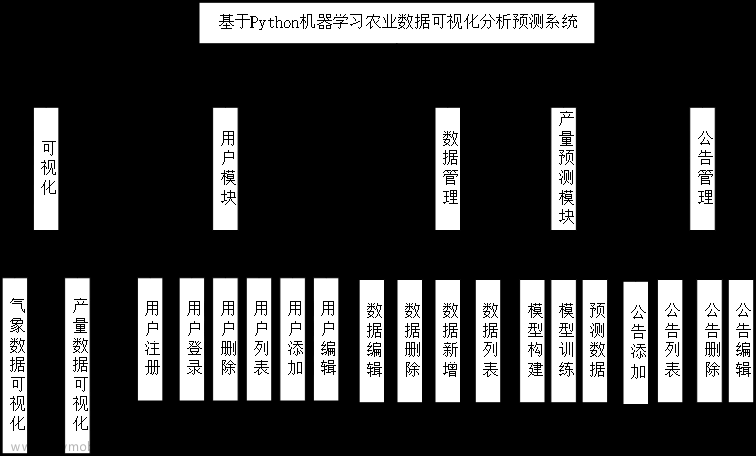
1.什么是XGBoost？

  GBDT，它是一种基于boosting增强策略的加法模型，训练的时候采用前向分布算法进行贪婪的学习，每次迭代都学习一棵CART树来拟合之前 $t-1$ 棵树的预测结果与训练样本真实值的残差。XGBoost对GBDT进行了一系列优化，比如损失函数进行了二阶泰勒展开、目标函数加入正则项、支持并行和默认缺失值处理等，在可扩展性和训练速度上有了巨大的提升，但其核心思想没有大的变化。

2.XGBoost的核心原理

2.1 如何构造目标函数？

  对于一个给定有 $n$ 个样本和 $m$ 个特征的数据集$D=\{(x_i,y_i)\}(|D|=n,x_i\in {\mathbb{R}}^m,y_i\in \mathbb{R})$。 树集成算法使用个数为 $K$ 的加法模型(如图1)来预测输出。

预测，这一家子人中每个人想玩游戏的意愿值?

  先训练出来第一棵决策树， 预测小男孩想玩游戏的意愿是 $2$， 然后发现离标准答案差一些，又训练出来了第二棵决策树， 预测小男孩想玩游戏的意愿是 $0.9$， 那么两个相加就是最终的答案$2.9$。

1.假设训练了 $K$ 棵树，对于第 $i$ 个样本的(最终)预测值为：
$${\hat{y}}_i=\varphi ({\mathbf{x}}_i)=\sum _{k=1}^K{f}_k({\mathbf{x}}_i),f_k\in F(1)$$
2.目标函数为(损失函数+模型复杂度(penalty))
$$obj=\sum _{i=1}^{n}l(y_i,{\hat{y}}_i)+\sum _{k=1}^K\Omega (f_k)(2)$$

Q：如何描述树模型的复杂度？

A：叶子结点的个数、树的深度、叶子结点值

3.加法模型

当训练第 $k$ 棵树时，前 $k-1$ 棵树都是已知的：

对于给定的样本 $x_i$而言：
$$\begin{array}{rl}& {\hat{y}}_i^{(0)}=0(defaultcase)\\ & {\hat{y}}_i^{(1)}=f_1(x_i)=f_1(x_i)+{\hat{y}}_i^{(0)}\\ & {\hat{y}}_i^{(2)}=f_2(x_i)+f_1(x_i)=f_2(x_i)+{\hat{y}}_i^{(1)}\\ & ⋮\\ & {\hat{y}}_i^{(k)}=f_k(x_i)+\cdots +f_2(x_i)+f_1(x_i)=f_k(x_i)+{\hat{y}}_i^{(k-1)}\end{array}$$
因为 $f$ 是决策树，而不是数值型的向量，所以我们不能使用梯度下降法进行优化。XGBoost是前项分布算法，我们可以通过贪心算法寻找局部最优解：每一次迭代寻找是损失函数降低最大的 $f$（CART树）。

此时的目标函数(目标：最小化)可以改写成：
$$\begin{array}{rl}obj& =\sum _{i=1}^{n}l(y_i,{\hat{y}}_i^{(k)})+\sum _{k=1}^K\Omega (f_k)\\ & =\sum _{i=1}^{n}l\left(y_i,{\hat{y}}_i^{(k-1)}+f_k(x_i)\right)+\sum _{j=1}^{K-1}\Omega (f_j)+\Omega (f_k)(3)\end{array}$$
其中 ${\hat{y}}_i^{(k-1)}、\sum _{j=1}^{K-1}\Omega (f_j)$ 均是常量。

当训练第 $k$ 棵树时，最小化目标函数有：
$$argmin\sum _{i=1}^{n}l\left(y_i,{\hat{y}}_i^{(k-1)}+f_k(x_i)\right)+\Omega (f_k)$$
注：

• $y_i$：真实值
• ${\hat{y}}_i^{(k-1)}$：前 $k-1$棵树的预测值
• $f_k(x_i)$：第 $k$ 棵树的预测值
• $\Omega (f_k)$：第 $k$ 棵树的复杂度

2.2 如何优化目标函数？

  在数学中，我们可以用泰勒公式近似 $f(x)$ ，具体如下式。XGBoost 对损失函数运用二阶展开来近似。
$$f(x_0+\Delta x)\approx f(x_0)+f^{(1)}(x_0)\Delta x+\frac{1}{2}{f}^{(2)}(x_0)\Delta x^2+\cdots +o(\Delta x^2)$$

对应XGBoost的损失函数，则有：
$$f(x+\Delta x)=l(y_i,{\hat{y}}_i^{(k-1)}+f_k(x_i))$$

$$\begin{array}{rl}obj& =\sum _{i=1}^{n}l\left(y_i,{\hat{y}}_i^{(k-1)}+f_k(x_i)\right)+\Omega (f_k)\\ & =\sum _{i=1}^n\left[l(y_i,{\hat{y}}^{(k-1)})+\frac{\partial l^{(1)}(y_i,{\hat{y}}^{(k-1)})}{\partial y_i}{f}_k(x_i)+\frac{1}{2}\frac{\partial l^{(2)}(y_i,{\hat{y}}^{(k-1)})}{\partial y_i}{f}_k(x_i{)}^2\right]+\Omega (f_k)\\ & =\sum _{i=1}^n\left[l(y_i,{\hat{y}}^{(k-1)})+g_i{f}_k(x_i)+\frac{1}{2}{h}_i{f}_k(x_i{)}^2\right]+\Omega (f_k)(4)\end{array}$$

上述式子转换为优化如下式子：
$$argmin\sum _{i=1}^n\left(g_i{f}_k(x_i)+\frac{1}{2}{h}_i{f}_k(x_i{)}^2\right)+\Omega (f_k)$$
注：当训练第 $k$ 棵树时， { h i , g i } \{h_i,g_i\} {hi​,gi​} 均是已知的。

2.3 如何将树结构引入到目标函数中？

新的目标函数为：
$$argmin\sum _{i=1}^n\left(g_i{f}_k(x_i)+\frac{1}{2}{h}_i{f}_k(x_i{)}^2\right)+\Omega (f_k)$$
现在是如何将 $f_k(x_i)$、$\Omega (f_k)$ 两者参数化？如何描述一棵树的复杂度？

树的参数化(如何表达一棵树?)

• 叶子结点的数值(leaf value)

  $w=(w_1,w_2,w_3)=(15,12,20)$

• $q(x)$ ：样本 $x$ 的位置(在哪个位置) 将输入 $x$ 映射到某个叶子结点上

  $q(x_1)=1$ $q(x_2)=3$ $q(x_3)=1$ $q(x_4)=2$ $q(x_5)=3$

根据上述信息可以得到：$f_k(x_i)=w_{q(x_i)}$

定义函数： I j = { i ∣ q ( x i ) = j } I_j=\{i|q(x_i)=j\} Ij​={i∣q(xi​)=j} 表示哪些样本落在第 $j$ 个叶子结点上。

I 1 = { 1 , 3 } I_1=\{1,3\} I1​={1,3}, I 2 = { 4 } I_2=\{4\} I2​={4}, I 3 = { 2 , 5 } I_3=\{2,5\} I3​={2,5}

树模型的复杂度：叶子结点的个数，树的深度，叶子结点的数值。则有：
$$\Omega (f_k)=\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2(5)$$
其中 $T$ 表示叶子结点的个数， $w_j$ 表示叶子结点的权重， $\gamma 、\lambda$ 均为超参数。

最终目标函数如下：
$$obj=argmin\sum _{i=1}^n\left(g_i{f}_k(x_i)+\frac{1}{2}{h}_i{f}_k(x_i{)}^2\right)+\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2(6)$$

现在就是求解最优解的问题。 为了使正则项和经验风险项合并到一起。我们把在样本层面上求和的经验风险项，转换为叶节点层面上的求和。
o b j = a r g   m i n   ∑ i = 1 n ( g i f k ( x i ) + 1 2 h i f k ( x i ) 2 ) + γ T + 1 2 λ ∑ j = 1 T w j 2 = a r g   m i n   ∑ j = 1 T [ g i w q ( x i ) + 1 2 h i w q ( x i ) 2 ] + γ T + 1 2 λ ∑ j = 1 T w j 2 = a r g   m i n   ∑ j = 1 T [ ∑ i ∈ I j g i w j + 1 2 ( ∑ i ∈ I j h i + λ ) w j 2 ] + γ T ( 7 ) \begin{align} obj &= arg\ min\ \sum\limits_{i=1}\limits^n\left(g_if_k(x_i)+\frac{1}{2}h_if_k(x_i)^2\right)+\gamma T+ \frac{1}{2}\lambda\sum\limits_{j=1}\limits^Tw_j^2\\[2ex] &= arg\ min\ \sum\limits_{j=1}\limits^T\left[g_iw_q(x_i)+\frac{1}{2}h_iw_q(x_i)^2\right]+\gamma T+ \frac{1}{2}\lambda\sum\limits_{j=1}\limits^Tw_j^2\\[2ex] &= arg\ min\ \sum\limits_{j=1}\limits^T\left[\sum\limits_{i\in I_j}g_iw_j+\frac{1}{2}(\sum\limits_{i\in I_j}h_i+\lambda)w_j^2\right]+\gamma T \qquad\qquad(7) \end{align} obj​=arg min i=1∑n​(gi​fk​(xi​)+21​hi​fk​(xi​)2)+γT+21​λj=1∑T​wj2​=arg min j=1∑T​[gi​wq​(xi​)+21​hi​wq​(xi​)2]+γT+21​λj=1∑T​wj2​=arg min j=1∑T​ ​i∈Ij​∑​gi​wj​+21​(i∈Ij​∑​hi​+λ)wj2​ ​+γT(7)​​
进一步简化表达，令 $\sum _{i\in I_j}{g}_i=G_j、\sum _{i\in I_j}{h}_i=H_j$， 注意这里 $G$ 和 $H$ 都是关于 $j$ 的函数:
o b j = a r g   m i n   ∑ j = 1 T [ ∑ i ∈ I j g i w j + 1 2 ( ∑ i ∈ I j h i + λ ) w j 2 ] + γ T = a r g   m i n   ∑ j = 1 T [ G j w j + 1 2 ( H j + λ ) w j 2 ] + γ T ( 8 ) \begin{align} obj &= arg\ min\ \sum\limits_{j=1}\limits^T\left[\sum\limits_{i\in I_j}g_iw_j+\frac{1}{2}(\sum\limits_{i\in I_j}h_i+\lambda)w_j^2\right]+\gamma T \\[2ex] &=arg\ min\ \sum\limits_{j=1}\limits^T\left[G_jw_j+\frac{1}{2}(H_j+\lambda)w_j^2\right]+\gamma T\qquad\qquad(8) \end{align} obj​=arg min j=1∑T​ ​i∈Ij​∑​gi​wj​+21​(i∈Ij​∑​hi​+λ)wj2​ ​+γT=arg min j=1∑T​[Gj​wj​+21​(Hj​+λ)wj2​]+γT(8)​​

可以看出，若一棵树的结构已经确定，则各个节点内的样本 $(x_i,y_i,g_i,h_i)$ 也是确定的，即 $G_j$，$H_j$ 、$T$ 被确定，每个叶节点输出的回归值应该使得上式最小，由二次函数极值点：
$$w_j^{\ast }=-\frac{G_j}{H_j+\lambda }$$
按此规则输出回归值后，目标函数值也就是树的评分如下公式，其值越小代表树的结构越好。观察下式，树的评分也可以理解成所有叶节点的评分之和：
$$ob{j}^{\ast }=-\frac{1}{2}\sum _{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T(9)$$

2.4 如何去寻找最优的树结构？

目标：寻找最优树的形状，这是一个暴力搜索的问题。如果树的结构已知的情况下，可以算出 $ob{j}^{\ast }$ 最小的树。通常来说不可能枚举出所有的树结构 $q$，而是用贪心算法，从一个叶子开始分裂，反复给树添加分支。决策树建立的过程就是一个不确定性减小的过程。

现有样本 { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 } \{1,2,3,4,5,6,7,8\} {1,2,3,4,5,6,7,8},建立一棵树。对于某个特征 $f_1$, 那么如何计算 $f_1(score)$ ?
$$f_1(score)=原来的不确定性(obj)-之后的不确定性(obj)$$

特征：$score=ob{j}_k^{\ast }(old)-ob{j}_k^{\ast }(new)$

由上述的结果可得：
$$ob{j}^{\ast }=-\frac{1}{2}\sum _{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T$$

$$\begin{array}{rl}& ob{j}^{\ast }(old)=-\frac{1}{2}\left[\frac{(G_7+G_8{)}^2}{H_7+H_8+\lambda }+\frac{(G_1+G_2+\cdots +G_6{)}^2}{H_1+H_2+\cdots +H_6+\lambda }\right]+\gamma \ast 2\\ & ob{j}^{\ast }(new)=-\frac{1}{2}\left[\frac{(G_7+G_8{)}^2}{H_7+H_8+\lambda }+\frac{(G_1+G_3+G_5{)}^2}{H_1+H_3+H_5+\lambda }+\frac{(G_2+G_4+G_6{)}^2}{H_2+H_4+H_6+\lambda }\right]+\gamma \ast 3\\ & ob{j}^{\ast }(old)-ob{j}^{\ast }(new)=\frac{1}{2}\left[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }+\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }\right]-\gamma \\ & G_L=G_1+G_3+G_5{G}_R=G_2+G_4+G_6\\ & H_L=H_1+H_3+H_5{H}_R=H_2+H_4+H_6\end{array}$$

因此分裂收益的表达式为：
$$Gain=\frac{1}{2}[\frac{({\sum }_{i\in I_L}gi{)}^2}{{\sum }_{i\in I_L}{h}_i+\lambda }+\frac{({\sum }_{i\in I_R}gi{)}^2}{{\sum }_{i\in I_R}{h}_i+\lambda }-\frac{({\sum }_{i\in I_I}gi{)}^2}{{\sum }_{i\in I_I}{h}_i+\lambda }]-\gamma (10)$$

$Gain$ 值越大，说明分裂之后能使得目标函数减小的越多，也就是越好。

3.分裂查找算法

3.1 贪心准则

XGBoost 会对特征值排序后遍历划分点，将其中最优的分裂收益作为该特征的分裂收益，选取具有最优分裂收益的特征作为当前节点的划分特征，按其最优划分点进行二叉划分，得到左右子树。 分裂收益的表达式为：
$$Gain=\frac{1}{2}[\frac{({\sum }_{i\in I_L}gi{)}^2}{{\sum }_{i\in I_L}{h}_i+\lambda }+\frac{({\sum }_{i\in I_R}gi{)}^2}{{\sum }_{i\in I_R}{h}_i+\lambda }-\frac{({\sum }_{i\in I_I}gi{)}^2}{{\sum }_{i\in I_I}{h}_i+\lambda }]-\gamma$$

上图是一次节点分裂过程，很自然地，分裂收益是树A的评分减去树B的评分。由（4），虚线框外的叶节点，即非分裂节点的评分均被抵消，只留下分裂后的LR节点和分裂前的S节点进行比较，因此分裂收益的表达式为：
$$Gain=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }]-\gamma$$

假设枚举年龄特征 $x_j$，考虑划分点 $a$，计算枚举 $x_j<a$ 和 $x_j\ge a$的导数和：

  对于一个特征，对特征取值排完序后，枚举所有的分裂点 $a$, 只要从左到右so面就可以枚举出所有分割的梯度 $G_L$ 和 $G_R$，计算增益。假设树的高度为 $H$，特征数为 $d$，则复杂度为 $O(Hdnlogn)$。其中排序为 $O(nlogn)$，每个特征都要排序乘以 $d$，每一层都要重复一遍操作，故要乘以高度 $H$。

3.2 近似算法

当数据量过大时,贪婪算法就不好用,因为要遍历每个分割点, 甚至内存都放不下， XGBoost总结了一个近似框架

• 近似算法的做法:
  • 根据特征分布的百分位数提出可能的候选分裂点
  • 将连续特征值映射到候选分割点分割出的箱子中
  • 计算出每个箱子中数据的统计量,根据统计量找到最佳的分割点
• 全局选择vs局部选择
  • 全局选择:建树之前求出所有特征可能的分裂点
  • 局部选择:在每次split之后求解特征的分裂点
  • 全局选择步骤少,但是需要足够的分裂点,因为每次split不更新分裂点

展开来看，特征分位数的选取还有 global 和 local 两种可选策略：

• global 在全体样本上的特征值中选取，在根节点分裂之前进行一次即可；
• local 则是在待分裂节点包含的样本特征值上选取，每个节点分裂前都要进行。

这两种情况里，由于global只能划分一次，其划分粒度需要更细

上面就是等频和等宽分桶的思路了 ,但是存在一个问题: 这样划分没有啥依据,缺乏可解释性

作者这里采用了一种对loss的影响权重的等值percentiles（百分比分位数）划分算法（Weight Quantile Sketch）。

3.3 加权分位数

  近似算法中很重要的一步是列出候选的分割点。通常特征的百分位数作为候选分割点的分布会比较均匀。作者进行候选点选取的时候，考虑的是想让loss在左右子树上分布的均匀一些，而不是样本数量的均匀，因为每个样本对降低loss的贡献可能不一样，按样本均分会导致分开之后左子树和右子树loss分布不均匀，取到的分位点会有偏差。

可以把公式(6)重写为：
$$\sum _{i=1}^n\frac{1}{2}{h}_i(f_t({\mathbf{x}}_i)+\frac{g_i}{h_i}{)}^2+\Omega (f_t)+constant$$

第一个就是$h_i$是啥？它为啥就能代表样本对降低loss的贡献程度？

$h_i$ 上面已经说过了，损失函数在样本处的二阶导数啊！

$$Ob{j}^{(t)}\approx \sum _{i=1}^n[g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)]+\sum _{i=1}^t\Omega (f_i)$$
为啥它就能代表第$i$个样本的权值啊？
$$\begin{array}{rl}{L}^{(t)}& \simeq \sum _{i=1}^n[l(y_i,{\hat{y}}_i^{(t-1)})+g_i{f}_t({\mathbf{x}}_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)]+\Omega (f_t)\\ & =\sum _{i=1}^n[\frac{1}{2}{h}_i\cdot \frac{2\cdot g_i{f}_t({\mathbf{x}}_i)}{h_i}+\frac{1}{2}{h}_i\cdot f_t^2(x_i)]+\Omega (f_t)\\ & =\sum _{i=1}^n\frac{1}{2}{h}_i[2\cdot \frac{g_i}{h_i}\cdot f_t({\mathbf{x}}_i)+f_t^2(x_i)]+\Omega (f_t)\\ & =\sum _{i=1}^n\frac{1}{2}{h}_i\left[\right(2\cdot \frac{g_i}{h_i}\cdot f_t({\mathbf{x}}_i)+f_t^2(x_i)+(\frac{g_i}{h_i}{)}^2)-\left(\frac{g_i}{h_i}{)}^2\right]+\Omega (f_t)\\ & =\sum _{i=1}^n\frac{1}{2}{h}_i\left[\right(f_t({\mathbf{x}}_i)+\frac{g_i}{h_i}{)}^2]+\Omega (f_t)+Constant\\ & =\sum _{i=1}^n\frac{1}{2}{h}_i\left[\right(f_t({\mathbf{x}}_i)-(-\frac{g_i}{h_i}){)}^2]+\Omega (f_t)+Constant\end{array}$$
后面的每一个分类器都是在拟合每个样本的一个残差$-\frac{g_i}{h_i}$, 其实把上面化简的平方损失函数拿过来就一目了然了。而前面的$h_i$可以看做计算残差时某个样本的重要性,即每个样本对降低loss的贡献程度。

第二个问题就是这个bin是怎么分的，为啥是0.6一个箱？

定义一个数据集 $D_k=(x_{1k},h_1),(x_{2k},h_2)...(x_{nk},h_n)$ ,示样本的第 $k$ 个特征的取值和其二阶梯度统计量。 可以定义一个排序方程 $r_k:\mathbb{R}\to [0,+\infty )$：
$$r_k(z)=\frac{1}{{\sum }_{(x,h)\in D_k}h}\sum _{(x,h)\in D_k,x<z}h$$
这里$z$的代表特征值小于$z$的那些样本。这个排名函数表示特征值小于$z$的样本的贡献度比例。假设 ，$z$是第一个候选点 ,那么$r_k(z)=\frac{1}{3}$,目标是找到相对准确候选的分割节点 { s k 1 , s k 2 , ⋯ s k l } \{s_{k1},s_{k2},⋯s_{kl}\} {sk1​,sk2​,⋯skl​},此处的$s_{k1}=\underset{i}{\min }{\mathbf{x}}_{ik},s_{kl}=\underset{i}{\max }{\mathbf{x}}_{ik}$,且 相邻两个桶之间样本贡献度的差距应满足下面这个函数：
$$\left|r_k(s_{k,j})-r_k(s_{k,j+1})\right|<ϵ,s_{k1}=\underset{i}{\min }{\mathbf{x}}_{ik},s_{kl}=\underset{i}{\max }{\mathbf{x}}_{ik}$$
$ϵ$ 控制每个桶中样本贡献度比例的大小 , 其实就是贡献度的分位点。 比如在上面图中我们设置了$ϵ=\frac{1}{3}$, 这意味着每个桶样本贡献度的比例是 $\frac{1}{3}$(贡献度的 $\frac{1}{3}$ 分位点), 而所有的样本贡献度总和是$1.8$， 那么每个箱贡献度是 $0.6$ ($1.8\ast ϵ$)，分为 $3$（$\frac{1}{ϵ}$）个箱， 上面这些公式看起来挺复杂，可以计算起来很简单，就是计算一下总的贡献度， 然后指定 $ϵ$, 两者相乘得到每个桶的贡献度进行分桶即可。这样我们就可以确定合理的候选切分点，然后进行分箱了 。

3.4 列采样与学习率

XGBoost为了进一步优化效果，在以下2个方面进行了进一步设计：

• 列采样(按层随机与按树随机)
  • 和随机森林做法一致，每次节点分裂并不是用全部特征作为候选集，而是一个子集。
  • 这么做能更好地控制过拟合，还能减少计算开销。
  • 按层随机：在每次分裂一个结点时，对同一层内的每个结点分裂之前，随机选择一部分特征，此时只需要遍历一部分特征，来确定最后分割点。
  • 按树随机：在建树之前就随机选择特征，之后所有的叶子结点均只使用这部分特征。
• 学习率
  • 也叫步长、shrinkage，具体的操作是在每个子模型前（即每个叶节点的回归值上）乘上该系数，不让单颗树太激进地拟合，留有一定空间，使迭代更稳定。XGBoost默认设定为 $0.3$。

3.5 特征缺失与稀疏性

XGBoost模型的一个优点就是允许特征存在缺失值。对缺失值的处理方式如下：

• 在特征k上寻找最佳 split point 时，不会对该列特征 missing 的样本进行遍历，而只对该列特征值为 non-missing 的样本上对应的特征值进行遍历，通过这个技巧来减少了为稀疏离散特征寻找 split point 的时间开销。

• 在逻辑实现上，为了保证完备性，会将该特征值missing的样本分别分配到左叶子结点和右叶子结点，两种情形都计算一遍后，选择分裂后增益最大的那个方向（左分支或是右分支），作为预测时特征值缺失样本的默认分支方向。

• 训练阶段:

  在训练过程中，如果特征$f_0$出现了缺失值，处理步骤如下：

  • 首先对于$f_0$非缺失的数据，计算出 $L_{split}$ 并比较大小，选出最大的 $L_{split}$，确定其为分裂节点（即选取某个特征的某个阈值）；

  • 然后对于**$f_0$缺失的数据**，将缺失值分别划分到左子树和右子树，分别计算出左子树和右子树的$L_{split}$，选出更大的 $L_{split}$，将该方向作为缺失值的分裂方向（记录下来，预测阶段将会使用）。
    $$L_{split}=\frac{1}{2}[\frac{({\sum }_{i\in I_L}gi{)}^2}{{\sum }_{i\in I_L}{h}_i+\lambda }+\frac{({\sum }_{i\in I_R}gi{)}^2}{{\sum }_{i\in I_R}{h}_i+\lambda }-\frac{({\sum }_{i\in I_I}gi{)}^2}{{\sum }_{i\in I_I}{h}_i+\lambda }]-\gamma$$

• 预测阶段:

  在预测阶段，如果特征$f_0$出现了缺失值，则可以分为以下两种情况：

  • 如果训练过程中，$f_0$出现过缺失值，则按照训练过程中缺失值划分的方向（left or right），进行划分；
  • 如果训练过程中，$f_0$没有出现过缺失值，将缺失值的划分到默认方向（左子树）。

4.工程优化

4.1 并行列块设计

  在建树的过程中，最耗时的部分是寻找最优的切分点，而在这个过程中，最耗时的部分是将数据排序。为了减少排序时间，提出了Block结构存储数据。

  XGBoost 将每一列特征提前进行排序，以块(Block)的形式储存在缓存中，并以索引将特征值和梯度统计量对应起来，每次节点分裂时会重复调用排好序的块。而且不同特征会分布在独立的块中，因此可以进行分布式或多线程的计算。

• Block中的数据以稀疏格式 CSC 进行存储。
• Block中的特征进行排序(不对缺失值排序)。
• Block中特征还需要存储指向样本的索引，这样才能根据特征的值来取梯度。
• 一个Block中存储一个或者多个特征值。

4.2 缓存访问优化

  特征值排序后通过索引来取梯度 $g_i$，$h_i$ 会导致访问的内存空间不一致(梯度信息是根据特征值排序存储的)，进而降低缓存的命中率，影响算法效率。

  为解决这个问题，在精确贪心算法中，XGBoost为每个线程分配一个单独的连续缓存区(buffer)，用来存放梯度信息(非连续–>连续)，然后计算梯度信息。在近似算法中，对 Block 的大小进行合理的设置。定义 Block 的大小为 Block 中最多的样本数。设置合适的大小是很重要的，设置过大容易导致命中率过低，过小容易导致并行化效率不高。

4.3 核外块计算

  数据量非常大的情形下，无法同时全部载入内存。XGBoost 将数据分为多个 blocks 储存在硬盘中，使用一个独立的线程专门从磁盘中读取数据到内存中，实现计算和读取数据的同时进行。
为了进一步提高磁盘读取数据性能，XGBoost 还使用了两种方法：文章来源地址https://www.toymoban.com/news/detail-714228.html

• 压缩 block，用解压缩的开销换取磁盘读取的开销。
• 将 block 分散储存在多个磁盘中，提高磁盘吞吐量。

5.XGBoost vs GBDT

• GBDT 是机器学习算法，XGBoost 在算法基础上还有一些工程实现方面的优化。
• GBDT 使用的是损失函数一阶导数，相当于函数空间中的梯度下降；XGBoost 还使用了损失函数二阶导数，相当于函数空间中的牛顿法。
• 正则化：XGBoost 显式地加入了正则项来控制模型的复杂度，能有效防止过拟合。
• 列采样：XGBoost 采用了随机森林中的做法，每次节点分裂前进行列随机采样。
• 缺失值：XGBoost 运用稀疏感知策略处理缺失值，GBDT无缺失值处理策略。
• 并行高效：XGBoost 的列块设计能有效支持并行运算，效率更优。

6.总结

• XGBoost是一种基于boosting增强策略的加法模型，训练时使用前项分布算法贪婪地学习一棵 cart树拟合前 $t-1$ 棵树的预测值与真实值之间的残差。使用二阶泰勒展开，目标函数加入正则化项、支持并行以及默认缺失值处理等优化。
• XGBoost的核心原理：如何构建目标函数–>如何优化目标函数–>如何引入树结构到目标函数？–>如何找到最优的树结构？
• XGBoost 的分裂查找算法：
  • 基本的贪心算法：先将特征值进行排序， 枚举出了所有特征上的所有可能的分裂节点，按顺序访问数据
  • 近似算法：解决数据量巨大时贪婪算法失效的问题。提出可能的候选分裂点(百分位数)–连续值映射到bin中–统计bin中的样本数量–筛选出最佳分裂点(分裂点给出时机：全局与局部)
  • 加权分位数： 通常特征的百分位数作为候选分割点的分布会比较均匀(理解)。(不同样本对loss的降低贡献的程度不同)
  • 稀疏性感知分裂查找： 稀疏感知算法处理缺失值,当特征值缺失时, 样本会被分类为默认方向。 最优的默认方向是从数据中学习出来
    心原理：如何构建目标函数–>如何优化目标函数–>如何引入树结构到目标函数？–>如何找到最优的树结构？

到了这里，关于XGBoost模型详解的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！