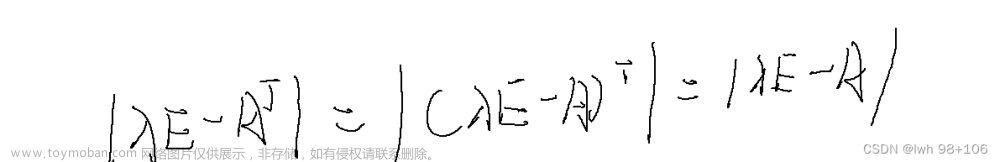作者:禅与计算机程序设计艺术 文章来源:https://www.toymoban.com/news/detail-714633.html
1.简介
1.1 什么是特征值?
在线性代数中,如果一个$n\times n$的方阵$A$满足如下两个条件之一:文章来源地址https://www.toymoban.com/news/detail-714633.html
- $A$存在实数特征值,即$\exists x\neq 0:Ax=kx$,其中$k\in \mathbb{R}$;
- $\lambda_{max}(A)\neq 0$($\lambda_{max}(A)$表示$A$的最大特征值),且$||x_{\lambda_{max}(A)}||=\sqrt{\frac{\lambda_{max}(A)}{\lambda_{min}(A)}}$,其中$x_{\lambda_{max}(A)}\neq 0$($x_{\lambda_{max}(A)}$表示$A$的最大特征向量)。那么称$A$为无奇异的。 显然,无奇异矩阵有唯一确定特征值的充要条件就是上述两个条件。而且,特征值具有大小的意义,不同的特征值对应着不同的特征空间,不同的特征空间对应着不同的几何变换。对于正定矩阵来说,所有特征值为正数。
1.2 什么是特征向量?
设$\det(A-\lambda I)=0$,其中$\lambda$是矩阵$A$的一个特征值,则称$x_{\lambda}$为矩阵$A$关于$\lambda$的特征向量。$\lambda$称为矩阵$A$的特征值,$x_{\lambda}$称为矩阵$A$的特征向量,对应的特征向量组成了$A$的特征空间。根据特征向量的定义可知,当$A$为实对称矩阵时,只有实数特征向量;而当$A$为复对称矩阵时,有实部和虚部均为零的特征向量。对于一般的$n\times n$的矩阵$A$,其特征空间由$n
到了这里,关于线性代数中矩阵的特征值与特征向量的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!