这篇具有很好参考价值的文章主要介绍了矩阵的范数和特征值之间的关系。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。
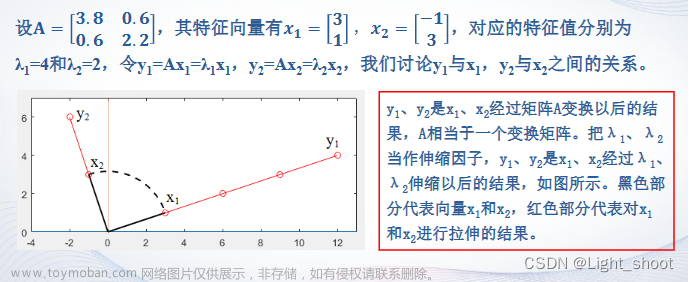
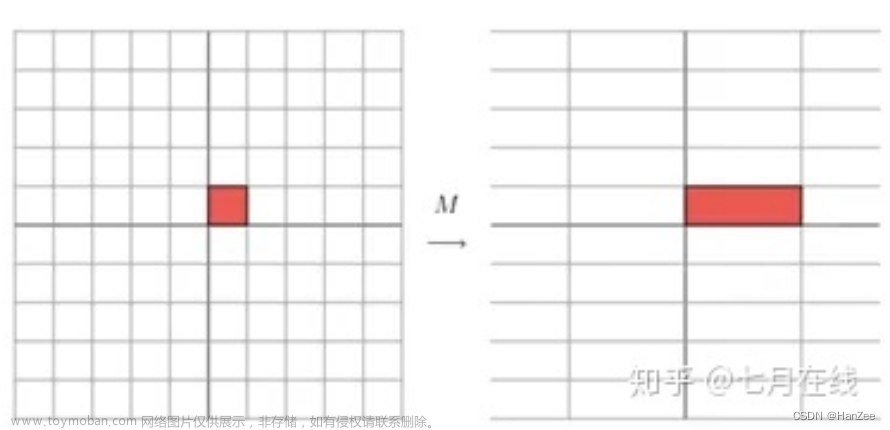
参考：文章来源：https://www.toymoban.com/news/detail-714790.html
linear algebra - Why is the norm of a matrix larger than its eigenvalue? - Mathematics Stack Exchange文章来源地址https://www.toymoban.com/news/detail-714790.html
到了这里，关于矩阵的范数和特征值之间的关系的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！
学习特征值和特征向量的定义和性质，我会采取以下方法： 1. 学习线性代数基础知识：特征值和特征向量是线性代数中的重要概念，需要先掌握线性代数的基础知识，例如向量、矩阵、行列式、逆矩阵、转置、内积、外积等基本概念。 2. 学习特征值和特征向量的定义：特征
设A是n阶方阵，如果存在常数λ和n维非零列向量x，使得等式Ax = λx 成立，则称λ为A的特征值，x是对应特征值λ的特征向量。 在MATLAB中，计算矩阵的特征值与特征向量的函数是eig，常用的调用格式有两种： E = eig（A）：求矩阵A的全部特征向量值，构成向量E。 [X，D] = eig（A）：
伸缩 一个矩阵其实就是一个线性变换，因为一个矩阵乘以一个向量后得到的向量，其实就相当于将这个向量进行了线性变换。比如说下面的一个矩阵： 因为这个矩阵M乘以一个向量(x,y)的结果是： 旋转 除了伸缩变换，也可以进行旋转变换。 上面的矩阵是对称的，所以这个变
应用：求幂，对角化，二次型，动力系统等等 通俗 向量α在矩阵A的线性变换作用下，保持方向不变，进行比例为λ的伸缩。 官方（注意是方阵） 特征方程 （λE-A)α = 0 （α!=0）特征向量不能为0，但是 特征值可以为0或虚数 。方程中λ的次数应与A的 阶数相同 ，否则不是
作者：禅与计算机程序设计艺术 在线性代数中，如果一个$ntimes n$的方阵$A$满足如下两个条件之一： $A$存在实数特征值，即$exists xneq 0:Ax=kx$,其中$kin mathbb{R}$； $lambda_{max}(A)neq 0$（$lambda_{max}(A)$表示$A$的最大特征值），且$||x_{lambda_{max}(A)}||=sqrt{frac{lambda_{max}(A)}{lambda_{
矩阵实际上是一种变换,是一种旋转伸缩变换（方阵） 不是方阵的话还有可能是一种升维和降维的变换 直观理解可以看系列超赞视频线性代数-哔哩哔哩_Bilibili 比如A= ( 1 2 2 1 ) begin{pmatrix}12\\\\21end{pmatrix} ( 1 2 2 1 ) x= ( 1 2 ) begin{pmatrix}1\\\\2end{pmatrix} ( 1 2 ) 我们给x左乘A实际
本篇特征值、特征向量笔记来源于MIT线性代数课程。 对于方阵而言，现在要找一些特殊的数字，即特征值，和特殊的向量，即特征向量。 给定矩阵A，矩阵A作用在向量上，得到向量Ax（A的作用，作用在一个向量上，这其实就类似于函数，输入向量x，得到向量Ax） 在这些向量
定理 1 设 λ 1 , λ 2 , ⋯ , λ m lambda_1,lambda_2,cdots,lambda_m λ 1 , λ 2 , ⋯ , λ m 是方阵 A boldsymbol{A} A 的 m m m 个特征值， p 1 , p 2 , ⋯ , p m boldsymbol{p}_1,boldsymbol{p}_2,cdots,boldsymbol{p}_m p 1 , p 2 , ⋯ , p m 依次是与之对应的特征向量，如果 λ 1 , λ 2 , ⋯ , λ
有矩阵 A 为 n 阶矩阵，Ax = λx （ λ 为一个实数，x为 n 维非零列向量 ），则称 λ 为方阵 A 的特征值， x 为特征向量； 1.2.1 公式 求特征值：使 | A - λE | = 0，其解的 λ 值即为矩阵 A 的特征值； 求特征向量： 使 ( A - λE )x = 0,设 x 为与 A 具有
} for(j=0;j=n;j++) { Matrix[j][k]+=temp*Matrix[j][i]; } } } } for(i=0;i=n;i++) { for(j=0;j=n;j++) { ret[i][j]=Matrix[i][j]; } } return n+1; } public static boolean EigenValue(double[][]Matrix,int n,int LoopNu,int Erro,double[][]Ret) { int i=Matrix.length; if(i!=n) { return false; } int j; int k; int t; int m; double[][]A=new double[n][n]; double erro=Math.po
